28.4.4. Ступінь чорноти і поглинальна спроможність газового об’єму
Одним з розповсюджених методів розрахунку теплообміну при випромінюванні є метод переходу від об’ємних характеристик випромінювання до характеристик, віднесених до поверхні, яка обмежує об’єм напівпрозорого середовища. Такими поверхневими характеристиками є ступінь чорноти eг і поглинальна спроможність Аг газового об’єму.
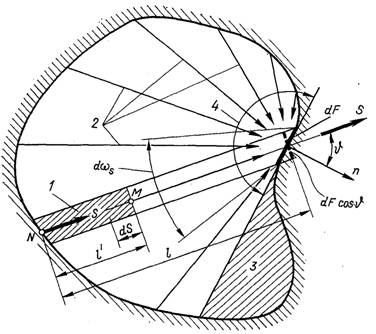
Рис.28.18. До визначення ступеня чорноти газового об’єму: 1 – стовп газу, який формує випромінювання у напрямку s у точці М; 2 – промені різної довжини, які досягають площадки dF; 3 – об’єм газу, випромінювання якого не потрапляє на площадку dF; 4 – півсфера, яка примикає до площадки зліва
Введемо ряд спрощень і проінтегруємо вираз (28.49) вздовж напрямку s від точки N граничної поверхні до довільної точки М, яка знаходиться в об’ємі середовища (рис.28.18). Будемо розглядати середовище, яке не розсіює промені (не запалений газ). При цьому коефіцієнт розсіювання дорівнює нулю, а коефіцієнт послаблення стає рівним коефіцієнту поглинання Кn = an. За такого уявлення рівняння (28.49) набуває вид
(28.51)
Якщо додатково прийняти, що радіаційні властивості середовища усталені в усьому об’ємі, то стає можливим інтегрування рівняння (28.51) у явному вигляді. Приведемо це рівняння до наступного виду
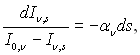
і після інтегрування, отримаємо:
(28.52)
де Іст.ефn – ефективне випромінювання стінки, тобто інтенсивність випромінювання, що падає від стінки на основу газового стовпа у точці N у напрямку s.
Перший доданок правої частини рівняння (28.52) представляє собою енергію випромінювання, що падає на основу газового стовпа у точці N і таку, що не поглинута до перерізу в районі точки М. Другий доданок відображає частку власного випромінювання газового стовпа у напрямку s, що залишається не поглинутою на шляху ℓў від точки N до точки М. Визначимо енергію, випромінювану власне газом (без урахування ефективного випромінювання стінок), і таку що пройшла через довільну площадку dF у довільних напрямках, що пересікають площину зліва направо (рис.28.18). Для цього необхідно інтенсивність випромінювання газу, яка виражається другим доданком правої частини рівняння (28.52), помножити на проекцію площадки dF на площину, перпендикулярну кожному з напрямків s, і на елементарний тілесний кут dws, а далі інтегрувати по всіх напрямках s, звідки променевий потік може надходити на площадку dF, тобто за півсферою, яка примикає до площадки dF зліва:
Розділимо обидві частини рівняння на dF і отримаємо величину поверхневої (півсферичної) густини потоку випромінювання, створену випромінюванням газового об’єму:
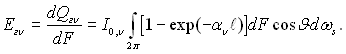(28.53)
Довжина шляху ℓ різна для кожного з напрямків s, і результат інтегрування залежить від конфігурації газового об’єму. Для півсферичного об’єму, який випромінює на центр основи, ℓ= R = const, тоді внаслідок інтегрування отримаємо:
У відповідності із законом Ламберта (28.19) добуток pІ0,n представляє собою спектральну півсферичну густину випромінювання абсолютно чорного тіла Е0,n при температурі газового об’єму, тоді
(28.54)
Можна ввести поняття ступеня чорноти газового об’єму як відношення поверхневої густини випромінювання, створюваного газовим об’ємом при деякій температурі, до густини випромінювання чорного тіла при тій же температурі:
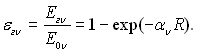(28.55)
У випадку об’ємів довільної конфігурації ступінь чорноти необхідно розраховувати для кожної точки на границі об’єму інтегруванням (28.53) з урахуванням залежності довжини променя від напрямку і далі осереднювати її за всією поверхнею.
Більш повний розгляд показує, що у загальному випадку ступінь чорноти газового об’єму можна записати в наступному виді:
(28.56)
де ℓеф – деяка ефективна довжина променя в газовому об’ємі даної конфігурації. Для випромінювання об’ємів на всю обмежуючу їх поверхню ефективна довжина променя з достатньою точністю виражається наближеним співвідношенням:
(28.57)
де V – об’єм випромінювання порожнини; F – поверхня, яка обмежує цю порожнину.
Для отримання виразу повного потоку випромінювання вводиться поняття повної чи інтегральної ступені чорноти газу, для цього необхідно інтегрувати (28.54) за всіма довжинами хвиль:
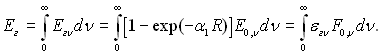
Інтегральна ступінь чорноти визначиться як відношення повного потоку випромінювання газу Ег до повного потоку випромінювання абсолютно чорного тіла при температурі, рівній температурі газу:
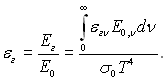(28.58)
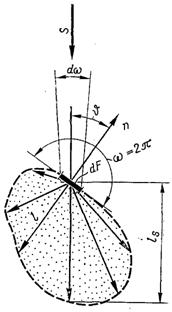
Рис.28.19. Поглинальна спроможність газового об’єму
Поглинальна спроможність газового об’єму (рис.28.19) можна ввести, розглянувши поглинання випромінювання, яке падає на елементарну площадку, розташовану в центрі основи об’єму, заповненого ізотермічним поглинальним газом.
У відповідності із законом Бугера (28.45) для променя довільного напрямку, що падає на площадку dF із зовні, інтенсивність поглинання випромінювання виражається залежністю:
(28.59)
Густина поглинутого випромінювання визначається в наслідок інтегрування (28.59) по півсфері (з боку падаючого випромінювання):
(28.60)
Поглинальна спектральна спроможність об’єму виразиться відношенням поглинутого випромінювання до падаючого:
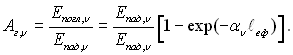(28.61)
Для отримання інтегральної поглинальної спроможності необхідно інтегрувати (28.60) за всіма частотами і розділити на густину повного потоку падаючого випромінювання:
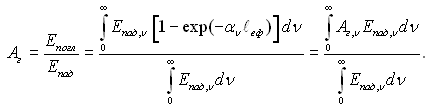(28.61)
Спектральна поглинальна спроможність газу залежить від стану газу, в тому числі і від його температури. Розподіл густини падаючого випромінювання за частотами залежить не від стану поглинального газу, а від характеристик випромінювача, який направляє проміння на газовий об’єм, від їх температури і спектральних характеристик.
Звідси виходить, що на відміну від ступеня чорноти поглинальна спроможність газу не є фізичною властивістю поглинального середовища, а залежить також і від зовнішніх умов. Тільки за умови термодинамічної рівноваги між падаючим випромінюванням і поглинальним середовищем, коли падаюче випромінення є абсолютно чорним, вирази (28.58) і (28.61) співпадають, що показує на справедливість за цих умов закону Кірхгофа для поглинального і випромінюваного середовищ:
Використовуючи поняття інтегральної ступені чорноти газу, можна формально випромінювання газового об’єму виразити рівнянням Стефана – Больцмана
(28.62)
Варто мати на увазі, що величина eг у цьому рівнянні сильно залежить від температури, так що густина випромінювання, яке проходить через границю газового об’єму, не пропорційна четвертій степені температури. Так, при інших рівних умовах, густина випромінювання диоксиду вуглецю пропорційна температурі у степені 3,5, а водню – в степені 3.
З рівнянь (28.56) і (28.61) видно, що при достатньо великій довжині хвилі ℓеф спектральні ступені чорноти і поглинальна спроможність газу в окремих смугах поглинання можуть досягати значення одиниці, тобто випромінювальні здатності шару газу у цих смугах можуть дорівнювати випромінювальній здатності абсолютно чорного тіла.
Однак повні випромінювальні характеристики газового об’єму завжди залишаються значно меншими для чорного тіла. Так гранична повна ступінь чорноти водяної пари при температурі 1000 °С становить біля 0,6, а двоокису вуглецю – біля 0,3.
При невисоких тисках поглинання променевої енергії газами підпорядковується закону Бера, згідно з яким коефіцієнт поглинання при даній температурі пропорційний тиску в поглинальному газі. У зв'язку з цим законом інформація про ступінь чорноти газів приводиться у вигляді залежностей eг = f(pℓеф, Т), де р – парціальний тиск газу; ℓеф – ефективна довжина променя у газовому об’ємі.
На рисунках 28.20 і 28.21 наведена ступінь чорноти двоокису вуглецю і водяної пари, а на рис.28.22 – ступінь чорноти шару повітря товщиною 0,1 м при різних тисках. Водяна пара проявляє відхилення від закону Бера вже при невеликих тисках, тому значення eг для Н2О, визначене з рис.28.21, необхідно множити на поправочний коефіцієнт b, який залежить від парціального тиску пари (рис.28.23).
Якщо газова суміш містить у собі декілька випромінюючих газів, то ступінь чорноти суміші знаходять додаванням ступенів чорноти компонентів. Із-за часткового перекриття смуг поглинання різних газів і, як наслідок, взаємного поглинання випромінювання дійсна ступінь чорноти виходить трохи меншою цієї суми. Так, для розрахунку ступеня чорноти продуктів згорання, які містять у собі СО2 і пари Н2О, використовується вираз:
(28.63)
Однак дані про значення поправок De є тільки для обмеженого діапазону температур і парціальних тисків, тому при наближених розрахунках поправкою нехтують.
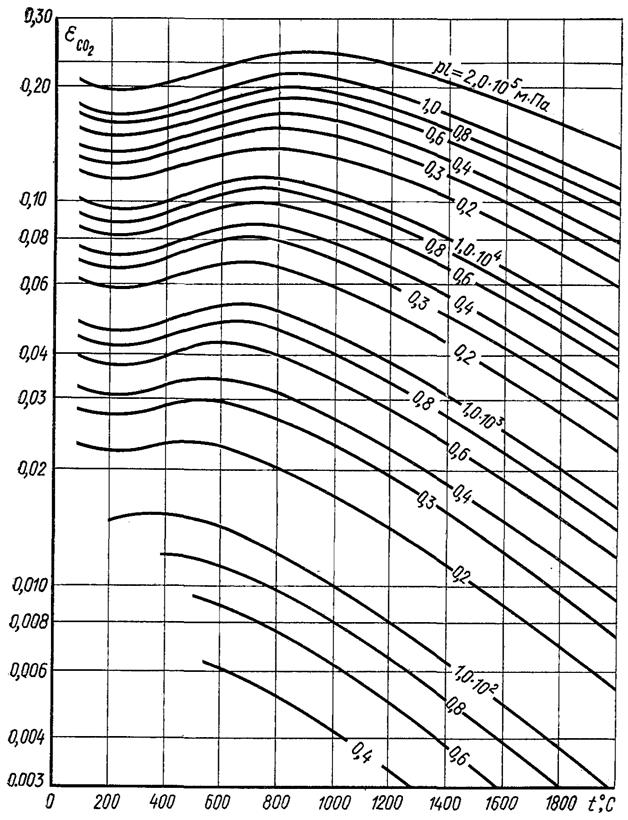
Рис.28.20. Ступінь чорноти двоокису вуглецю
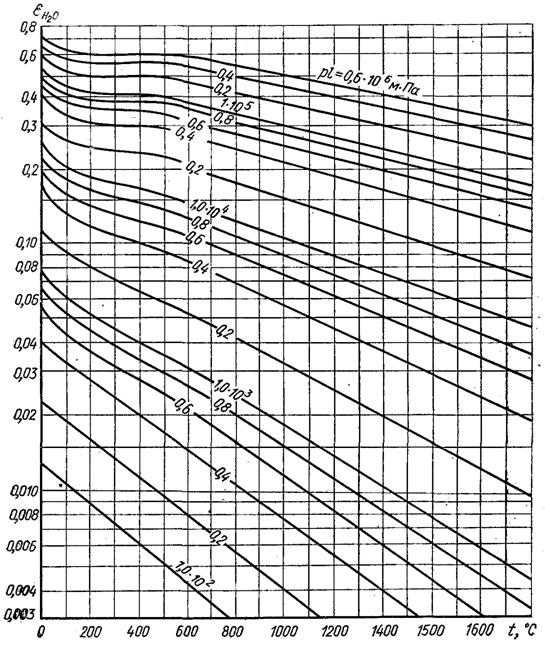
Рис.28.21. Ступінь чорноти водяної пари
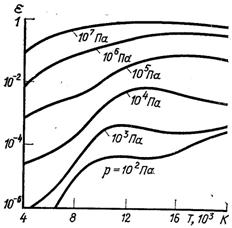
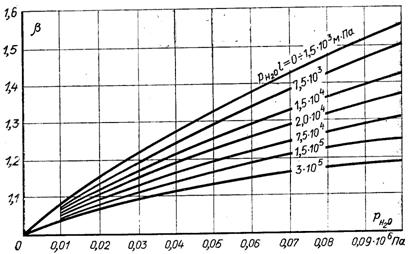
Рис.28.22. Поправка впливу тиску на ступінь чорноти водяної пари
Рис.28.23. Ступінь чорноти шару повітря товщиною 0,1 м при тиску 0,102 МПа
28.4.5. Радіаційний теплообмін між газом і оболонкою
Радіаційний теплообмін між газом і оточуючою його оболонкою, є наслідком багаторазових поглинань і відбивань стінкою потоку, який випромінюється газом, і багаторазових поглинань і пропускань газом потоку, випромінюваного стінкою (рис.28.24). Якщо при цьому як стінку, так і газ розглядати як сірі тіла зі ступенем чорноти, яка не залежить від температури, то променевий тепловий потік можна знайти по формулі (28.26), отриманій для розрахунку теплообміну між твердим тілом і оточуючою його оболонкою при малому зазорі між ними:
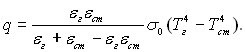(28.64)
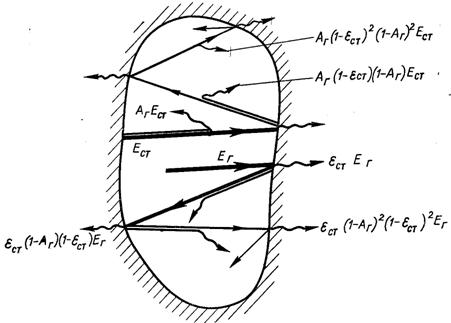
Рис.28.24. Теплообмін між газом і оболонкою
Значні ускладнення виникають при необхідності враховувати селективний характер випромінювання і поглинання газів, який призводить до суттєвої залежності степені чорноти газу від його температури і поглинальної спроможності газу від температури падаючого на нього випромінювання. Розглянемо випадок (рис.28.24), коли ступінь чорноти стінки не залежить від температури і частоти випромінювання (сіра оболонка), а ступінь чорноти газу і його поглинальна спроможність залежить від температури газу і від температури падаючого на газ випромінювання, але не залежить від частоти (наближення сірого газу).
Густина випромінювання газового об’єму з температурою Тг і ступенем чорноти eг на границі з оболонкою становить Ег = eгs0Тг4. З цієї кількості стінкою поглинається частина, пропорційна поглинальній спроможності (ступеню чорноти) стінки і рівна eстЕг. Енергія, рівна (1 – eст)Ег, відбивається назад в об’єм, де частина її поглинається, а залишок у кількості (1 – Аг)(1 – – eст)Ег, пропускається на стінку. Друга порція енергії, яка поглинута стінкою, становить eст(1 – Аг)(1 – eст)Ег. Розглядаючи наступні ступені: відбивання – часткового пропускання газом – поглинання стінкою і т. д., приходимо до висновку, що порції випромінювання газового об’єму, які поглинуті стінкою, виражаються як члени спадної безмежної геометричної прогресії із знаменником (1 – Аг)(1 – eст). Загальна кількість випромінювання газу, поглинутого стінкою, виражається сумою членів цієї прогресії:
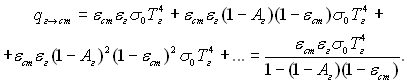(28.65)
Власне випромінювання Ест = eстs0Тст4 частково поглинається газом: пропущена газом частина частково поглинається стінкою, а частина відбивається у газовий об’єм, де знову поглинається деяка його частина і т. д. Аналогічні попереднім міркування приводять до висновку, що із загальної кількості випромінювання стінкою, кількість поглинута газом виразиться також сумою членів спадної геометричної прогресії:
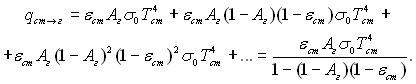(28.66)
Результуючий променевий теплообмін між газовим об’ємом і оточуючою його оболонкою визначається як різниця величин виражених формулами (28.65) і (28.66):
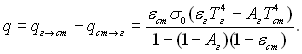(28.67)
Необхідно мати на увазі, що eг представляє собою ступінь чорноти газового об’єму при температурі газу Тг, а Аг – поглинальну спроможність газу по відношенню до випромінювання, яка характеризується температурою стінки Тст. Зазвичай приймають, що закон Кірхгофа для газу приблизно виконується і при відсутності термодинамічної рівноваги між газом і випромінюванням, тому Аг,Тст = eг,Тст.
Значення eг і Аг визначаються для відповідних температур за (28.63). У розрахунковій практиці вираз (28.67) записують у більш простій формі, вводячи поняття ефективного ступеня чорноти стінки:
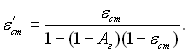(28.68)
Тоді
(28.69)
Як видно з виразу (28.68) і рис.28.25, ефективна ступінь чорноти стінки більша за дійсну ступінь чорноти. Це наслідок багатократних повторних поглинань випромінювання, відбитих стінкою: відомо, що ефективна ступінь чорноти замкненої порожнини, заповненої прозорим середовищем, дорівнює одиниці. У цьому випадку для практичних розрахунків використовують наступну залежність:
(28.70)
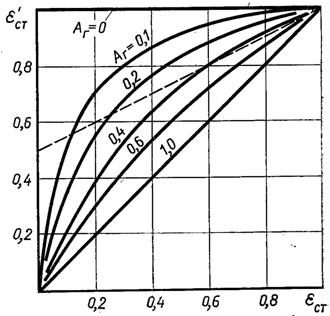
Рис.28.25. Ефективна ступінь чорноти замкненої оболонки: ––––– – розрахунок по формулі (28.68); – – – – – розрахунок по формулі (28.70)
Ясно, що ця рекомендація задовільна тільки в обмеженому діапазоні значень eст і Аг і може призвести до суттєвої помилки, особливо при малій ступені чорноти поверхні, яка сприймає промені.
28.4.6. Особливості теплообміну в камерах згорання
При згоранні палива у камерах згорання (топках) парогенераторів, нагрівальних пристроїв, газових турбінах, ракетних двигунах та ін. утворюється факел полум’я, а далі потік гарячих продуктів згорання, з яких значна кількість теплоти передається випромінюванням більш холодним стінкам камери згорання. Розрахунок радіаційного теплообміну в камерах згорання представляє собою дуже великі труднощі, викликані складністю фізичних умов, у яких відбувається процес горіння і теплообміну. Ці труднощі викликані, по-перше, складністю випромінювальних характеристик середовища і їх різкій залежності від умов процесу; по-друге, значною нерівномірністю температурних полів в об’ємі камери; по-третє, великою неоднорідністю поглинальних характеристик і температури сприймаючих тепло поверхонь, які бувають покриті шаром окислів, пилу, сажі, шлаку.
У загальному випадку випромінювання полум’я складається з випромінювання газів (при горінні вуглеводних палив – це головним чином диоксид вуглецю і водяна пара), випромінювання частинок сажі і спалюваного палива (коксу) і частинок золи, які у найбільш гарячих зонах факелу полум’я плавляться, а по мірі охолодження потоків газу твердіють. Відносний вклад кожного з випромінювачів у загальне випромінювання залежить від виду палива, способу і умов його спалювання, від розміщення розглядуваного об’єму в камені згорання.
Вид полум’я залежить від того, якими випромінювачами визначають його радіаційні властивості.
Несвітне полум’я утворюється при спалюванні газоподібного палива за умови хорошого перемішування горючого газу з окислювачем. Випромінювання несвітного полум’я (а також згаслих продуктів спалювання газу) обумовлене майже виключно радіаційними властивостями диоксиду вуглецю і водяної пари.
Світне полум’я утворюється при спалюванні рідких вуглеводних палив (мазуту, гасу та ін.) без їх попереднього випаровування. У такому полум’ї поряд з трьохатомними газами випромінюють і частинки сажі, які утворюються при температурному розкладанні палива на початковій стадії горіння і поступово вигоранні до кінця факелу.
Півсвітне полум’я утворюється при спалюванні твердого палива у пиловидному стані. У цьому випадку до випромінювання трьохатомних газів добавляється випромінювання порівняно крупних коксових частинок і частинок золи, інколи і випромінювання сажі.
Полум’я (крім несвітного) представляє собою випромінюване, поглинальне і розсіювальне (мутне) середовище. Радіаційні характеристики цих середовищ сильно залежать від концентрації, розмірів і фізичних властивостей частинок, а також від температури.
У практиці інженерних розрахунків радіаційного теплообміну у камерах згорання отримали розповсюдження два основних методи. Перший ґрунтується на застосуванні рівняння Стефана – Больцмана, другий – на застосуванні теорії подібності при узагальненні дослідних даних по теплообміну і на використанні емпіричних рівнянь подібності.
Для випадку, коли усі стінки камери згорання покриті сприймаючою тепло поверхнею з однаковою температурою Тст, прийнята променева теплота Qn може бути виражена формулою:
(28.71)
Ефективна ступінь чорноти системи факел – поверхня сприйняття тепла ак виражається через ефективну поглинальну здатність поверхні апр і поглинальну здатність факела аф:
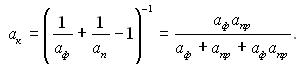(28.72)
У свою чергу, величина аф залежить від ефективної довжини променя ℓеф, загального тиску р газів у камері згорання і коефіцієнта послаблення променів топічним середовищем К:
(28.73)
При несвітному полум’ї цей коефіцієнт можна розраховувати по формулі:
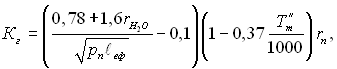(28.74)
де ТІт – температура газів на виході з топки; 
сумарна об’ємна частка трьохатомних газів; рп = рrn – сумарний парціальний тиск трьохатомних газів.
При світному полум’ї промені додатково послаблюються частинками сажі, тоді
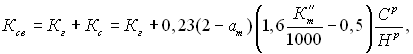(28.75)
де ат – коефіцієнт надлишку повітря у топці; С р і Н р – вміст вуглецю і водню у топці.
При запиленому півсвітному полум’ї ураховують послаблення променя частинками золи і коксу, тобто
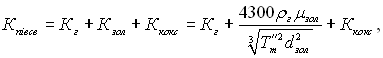(28.76)
де rг – густина газів; mзол – концентрація частинок золи; dзол – середній діаметр частинок золи; Ккокс = 0,02...0,10 у залежності від виду палива і способу його спалювання.
Ефективна температура факелу середовища топки Тф на 2...25% вища за температуру на виході з камери згорання в залежності від роду палива і умов згорання. Температура повернутої в бік топки забрудненої відкладеннями сприймаючої тепло поверхні Тст повинна визначатися з урахуванням густини теплового потоку і термічного опору шару забруднення. Розмір поверхні, яка сприймає променевий потік F, розраховується за конструктивними даними топки.
Рівняння подібності для розрахунку радіаційного теплообміну пов’язує безрозмірну температуру на виході з топки qІт = ТІт /Тад (не визначальне число) з визначальними числами, такими як число Больцмана (Во), ступінь чорноти топки ат і параметр М, який залежить від розподілу температури по довжині топки (М » 0,5):
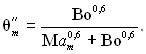(28.77)
Число Больцмана виражає співвідношення між теоретичною ентальпією продуктів згорання палива і густиною максимально можливого променевого потоку від факелу:
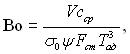(28.78)
де Vccp – середня теплоємність продуктів згорання; y – коефіцієнт теплової ефективності сприймаючих тепло поверхонь, він ураховує їх конструкцію і забрудненість, його значення від 0,1 до 0,65; Fcm – поверхня стін камери топки; Тад – температура газів, яка була б при згоранні без теплообміну (адіабатна температура). Ступінь чорноти топки пов’язана зі ступенем чорноти факелу аф, яка визначається за формулами (28.74)...(28.76), співвідношенням
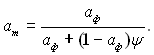(28.79)
У зв'язку з тим, що ряд вихідних величин залежить від кінцевої температури газів, то розрахунок за обома способами виконується методом послідовних наближень.
Складним чи комбінованим теплообміном називають процес переносу тепла, при якому випромінювання відіграє суттєву роль поряд з теплопровідністю і конвекцією. Повна система рівнянь, яка описує складний теплообмін, включає в себе диференціальні і інтегрально-диференціальні рівняння і не знаходить аналітичного розв’язку. Навіть при сучасних можливостях числового рішення приймається ряд спрощень і допущень, які призводять до наближеного, оціночного розв’язку складної задачі. Можна виділити три випадки складного теплообміну.
Радіаційний теплообмін між потоком випромінювання газу і стінками каналу. При цьому зазвичай нехтують теплопровідністю і вважають, що конвекцією теплота переноситься тільки у напрямку руху потоку. На відміну від спрощеної задачі розглянутої раніше (нерухомий газ, постійна в об’ємі газу температура), у цьому випадку враховується нерівномірний розподіл температури газу по перерізу каналу і по його довжині, що викликається теплообміном. При цьому кількість переданої випромінюванням теплоти не зростає монотонно з ростом ступеня чорноти газового об’єму, а має певне максимальне значення. Зменшення кількості переданої теплоти при великій поглинальній спроможності середовища пояснюється тим, що охолоджені пристінні шари мало прозорого газу виконують роль екрану, не пропускають на холодну стінку випромінювання середніх шарів газу.
Радіаційно-кондуктивний теплообмін. Теплота переноситься від одної твердої поверхні до другої через нерухоме поглинальне (у загальному випадку і таке, що розсіює енергію) середовище як випромінюванням, так і теплопровідністю. У випадку середовища, яке не розсіює енергію задача характеризується п’ятьма безрозмірними параметрами, а саме: характерною оптичною товщиною шару середовища KL, ступенями чорноти поверхонь eст1 і eст2, відносною температурою “холодної” поверхні q2 = Т2/Т1 і параметром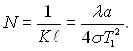 
Останній параметр характеризує взаємну інтенсивність переносу тепла теплопровідністю і випромінюванням: при N ® Ґ теплота переноситься тільки теплопровідністю, при N ® 0 – тільки випромінюванням. У зв'язку із складністю задачі порівнянно прості рішення отримуються тільки для деяких граничних випадків.
1) Оптично тонкий шар KL ® 0. Випромінювання не поглинається середовищем, а переноситься від одної поверхні до другої, як у випадку діатермічного середовища. Повний тепловий потік знаходять простим додаванням променевого і кондуктивного потоків q = qпром + qконд. Для плоского шару qпром визначається по формулі (28.67), а qконд – по (1.6), тоді
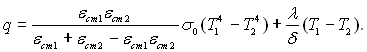(28.80)
2) Оптично товстий шар KL ® Ґ. Вплив радіаційних властивостей поверхонь розповсюджується всередину об’єму на відстань набагато меншу, ніж характерний розмір системи, а характеристики поля випромінювання у довільній точці об’єму залежать тільки від умов у цій точці чи біля неї. Внаслідок цього рівняння переносу випромінювання з інтегрально-диференціальних перетворюються у диференціальні. У цьому випадку повний потік складається з радіаційного і кондуктивного потоків. Однак на відмінність від (28.80) радіаційний потік виражається тепер по-іншому. Для плоского шару вираз має наступний вид:
(28.81)
3) Кінцева оптична товщина шару (загальний випадок). Випромінювання від поверхні глибоко проникає в об’єм середовища, де частково поглинається, і чинить вплив на розподіл температури. Це, у свою чергу, змінює умови передачі теплоти теплопровідністю, внаслідок чого сумарний тепловий потік не можна отримати простим додаванням радіаційного і кондуктивного потоків, розрахованих незалежно один від другого. Вибір одного чи іншого методів рішення системи інтегрально-диференціальних рівнянь у значному ступені залежить від конкретних умов задачі.
Радіаційно-конвективний теплообмін. Це найбільш складний випадок, коли рівняння переносу променевої енергії повинні рішатися разом з рівняннями руху і конвективного теплообміну. Задача настільки складна, що до сих пір зроблені тільки спроби аналізувати деякі дуже спрощені випадки. Для практичних розрахунків використовують принцип незалежності конвективного і променевого потоків один від одного, що буде вірним у випадку, коли один з них значно менший за інший. Для урахування тепловіддачі випромінюванням до коефіцієнта тепловіддачі конвекцією, розрахованому звичайним шляхом, тобто без урахування впливу радіаційного теплообміну на профілі швидкості і температури, рекомендується додавати коефіцієнт тепловіддачі випромінювання aп. У цьому разі коефіцієнт тепловіддачі від газів до зовнішньої стінки труб становить
a = aк + aп. (28.82)
У цьому виразі aп – умовний коефіцієнт тепловіддачі випромінюванням, отриманий діленням променевого потоку на різницю температур між газом і поверхнею труб:
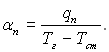(28.83)
