28.4. Радіаційний теплообмін у поглинальних і випромінюючих середовищах

28.4.1. Особливості випромінювання у напівпрозорих середовищах

У попередніх параграфах розглядався перенос енергії випромінювання між поверхнями твердих тіл, які розділені між собою прозорим (діатермічним) середовищем. Дійсно діатермічною, не спроможною до взаємодії з випромінюванням середовища є абсолютний вакуум. Але у багатьох випадках простір, заповнений газом, також можна вважати практично діатермічним, прозорим. Велике значення у техніці починають відігравати і такі пристрої, в яких змінюються об’єми, заповнені середовищами активними стосовно випромінювання, тобто середовищами, які спроможні випромінювати, поглинати і розсіювати електромагнітні хвилі. Такі середовища називають напівпрозорими. Найбільше значення мають три види напівпрозорих середовищ.

Газові середовища. Теплове випромінювання газів, тобто випромінювання електромагнітних хвиль внаслідок зіткнення молекул під час їх хаотичного теплового руху, виникає тільки у тому випадку, якщо енергія зіткнення перевищує енергію дозволену квантовими закону переходу молекули (атома, електрона) з одного енергетичного рівня на інший. Те саме справедливе по відношенню поглинання випромінювання газами. У молекулах газів можливі різні види енергетичних переходів: коливні (зміна середньої відстані між атомами в молекулі), обертальні, електронні (при іонізації). Випромінювання чи поглинання електромагнітної енергії при коливних і обертальних переходах можливе, коли молекули газу електрично несиметричні. Енергія цих переходів така, що відповідне випромінювання знаходиться в інфрачервоній і далекій інфрачервоній (а інколи і в мікро радіохвильовій) областях спектру. Коливально-обертальні переходи можуть збуджуватися при порівнянно невисоких температурах (до декількох сотень градусів).

Для симетричних молекул таких газів, як кисень, водень, азот та ін., а також для одноатомних частинок (інертні гази, пари металів) випромінювання можливе тільки при електронних переходах (зв’язано-зв’язані переходи електрона з одної орбіти на іншу чи зв’язано-вільні переходи при дисоціації і іонізації). Випромінювання, яке супроводжує ці переходи, лежить в ультрафіолетовій області спектру, а їх енергія настільки велика, що вона у більшості газів збуджується тільки при дуже високих температурах, які вимірюються тисячами градусів. У зв'язку з цим часто говорять, що прості гази (азот, водень, гелій та ін.) прозорі для теплового випромінювання, і при розрахунках приймається до уваги тільки випромінювання багатоатомних газів з несиметричними молекулами – діоксид вуглецю, водяна пара, вуглеводні та ін. Варто пам’ятати про умовність таких тверджень: при температурі порядку 5000...10000 К і більш високих і прості гази стають напівпрозорі.

Гази без пилу не розсіюють і не відбивають випромінювання, тому їх радіаційні властивості визначаються поглинальними характеристиками, які залежать від частоти випромінювання і стану газу, а також від геометрії газового об’єму. Оскільки коливні, обертальні і електронні переходи відбуваються у газах при помірних температурах, які здійснюються тільки між дозволеними рівнями, енергія виходу при переходах фотонів знаходиться в порівнянно вузьких межах, тобто енергія випромінювання газів знаходиться в декількох вузьких смугах частот електромагнітних коливань. Аналогічна картина спостерігається і при поглинанні випромінювання газом: енергія поглинається тільки у смугах частот, які відповідають енергії дозволених переходів. Випромінювання і поглинання газів тому називають вибірковим чи селективним. Кількість і положення смуг у спектрі визначається природою газу, а ширина смуг і розподіл інтенсивності випромінювання чи поглинання частотою в межах смуги залежить від стану газу (температури, тиску) і від довжини шляху променя в газі.

У процесі іонізації і рекомбінації молекул і атомів газів, що має місце при досить високих температурах, відбуваються зв’язано-вільні переходи, коли випущений (поглинутий) фотон може мати практично любу енергію, а відповідне йому випромінювання – любу частоту. Тому з ростом температури газу в його спектрі все більшу роль починають відігравати суцільні ділянки випромінювання і поглинання променевої енергії.

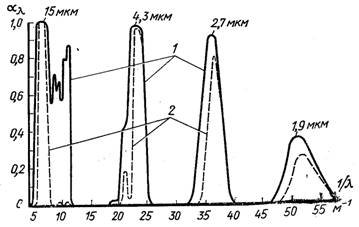
Рис.28.13. Залежність поглинальної спроможності СО₂ від довжини хвилі при р = 0,1 МПа і температурі Т, К: 1– 830; 2 – 300

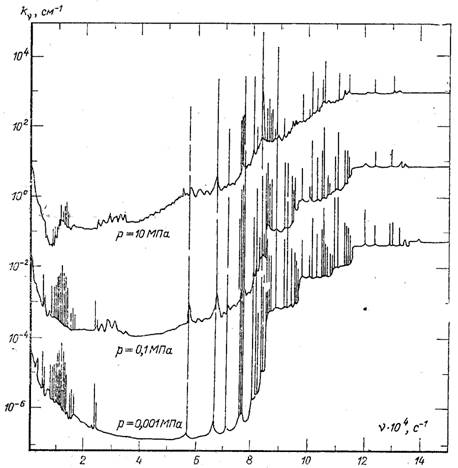
Рис.28.14. Залежність коефіцієнта поглинання повітря від частоти при Т = 10000 К і різних тисках (вертикальні лінії відповідають спектральним лініям, де поглинання на 2...4 порядки більше, ніж у сусідніх областях спектру)

На рис.28.13 наведений спектр поглинання діоксид вуглецю, а на рис.28.14 – спектр поглинання повітрям при високих температурах і різних тисках. Графіки показують Наскільки сильно і нерегулярно змінюється коефіцієнт поглинання газів у залежності від частоти, температури і тиску. Це дуже ускладнює і робить часто ненадійним використання спектральних даних для практичних розрахунків радіаційного теплообміну. Більш зручним є використання спектральних чи інтегральних характеристик ступені чорноти газового об’єму (28.55) і (28.58), при цьому останню можна отримати чи інтегруванням спектральних кривих по частоті, чи дослідним вимірюванням променевого потоку, який виходить з газу.

Запорошені середовища. Запорошеними чи, точніше, двофазними називають середовища, в яких тверді чи рідкі частинки зважені в діатермічному чи випромінюваному газі. Розміри частинок можуть бути самими різними – від декількох міліметрів до декількох мікрон. Типовими є випадки, коли розміри частинок в основному значно більші, ніж середня довжина хвиль випромінювання при даній температурі. Типовими прикладами запорошених середовищ є продукти згорання твердого природного палива із зваженими в них частинками золи і полум’я палива.

Світне полум’я. Це напівпрозоре середовище представляє собою потік випромінюваних газів у суміші з твердими випромінюючими частинками. На відміну від запорошених середовищ полум’я містить випромінюючі частинки, розміри яких співрозмірні з довжиною хвиль теплового випромінювання і менше від них – від часток мікрона до сотень ангстрем. Це частинки сажі, які утворюються під час горіння в наслідок термічного розкладу вуглеводневих молекул.

Характерною особливістю запорошених потоків і полум’я (а також аерозолів) є їх властивість у значній мірі розсіювати випромінювання, яке проходить через них, внаслідок цього подібні середовища часто називають мутними. До них можна віднести і деякі тверді тіла – скло і кристали, а також рідини, які знаходяться в порівняно тонких шарах.

28.4.2. Об’ємне випромінювання і поглинання

У загальному випадку об’єм напівпрозорого середовища може випромінювати власні промені, а також поглинати і розсіювати випромінювання, яке надходить із зовні через границю об’єму. В наслідок взаємодії випромінювання з зовнішнім середовищем в об’ємі формується поле випромінювання, яке характеризується певним розподілом електромагнітної енергії за частотами і у просторі.

Як і випадку випромінювання з поверхні непрозорого тіла, при об’ємному випромінюванні варто розрізняти спектральні (монохроматичні) характеристики випромінювання, які відносяться до випромінювання певної частоти (точніше, до випромінювання, яке знаходиться у безмежно малому інтервалі частот від n до n + dn), і повні (інтегральні характеристики), які відносяться до всього діапазону частот. У випадку адитивних величин перехід від спектральних до інтегральних характеристик виконується простим інтегруванням спектральної величини за частотою, як, наприклад, це було зроблено при переході від формули Планка до формули Стефана – Больцмана (28.12). Але багато величин за своїм фізичним змістом не допускають такого додавання і вимагають введення деяких умовних (ефективних) значень із складними законами осереднення. Прикладами можуть бути введені у подальшому інтегральний коефіцієнт поглинання, оптична довжина променя і інші величини. Далі розглядаються спектральні характеристики, які відмічаються індексом n.

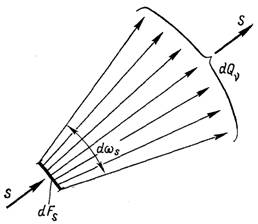
Рис.28.15. До поняття спрямованої інтенсивності випромінювання

Найбільш детальною характеристикою випромінювання в об’ємі є спектральна інтенсивність випромінювання (яскравість випромінювання) In_.s, яка визначається як потік енергії випромінювання dQn даної частоти n, який проходить у даному напрямку s (рис.28.15) через елементарну площадку dF_s, перпендикулярну напрямку s у межах елементарного тілесного кута dw, віднесену до одиниці поверхні, одиниці частотного інтервалу і одиниці тілесного кута:

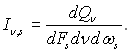(28.38)

У загальному випадку інтенсивність випромінювання залежить від положення точки в об’ємі середовища, від частоти, від напрямку, в якому розглядається потік випромінювання. У нестаціонарних процесах вона залежить і від часу.

Визначивши значення інтенсивності випромінювання у кожній точці об’єму для всіх напрямків і частот, розрахувати усі інші характеристики випромінювання, у тому числі і кількість променевої енергії, яка проходить між об’ємом і оточуючою його поверхнею, а також між окремими поверхнями, які оточують об’єм.

Власне випромінювання середовища складається із спонтанного випромінювання, викликаного випадковими переходами частинок із збудженого стану до більш низьких енергетичних станів, і індукційного (вимушеного) випромінювання, викликаного переходом частинок на низькі рівні під дією зовнішнього електричного поля. Спонтанне випромінювання залежить від природи речовини і її термодинамічного стану, а індукційне випромінювання – ще і від інтенсивності зовнішнього поля (від падаючого випромінювання). Власне випромінювання може бути нерівномірно розподілене за різними напрямками, які виходять з даного об’єму. З розрахункової точки зору зручно розглядати індукційне випромінювання як від’ємне поглинання і враховувати його разом з дійсним поглинанням. Тому під випромінюванням середовища розуміють спонтанне об’ємне випромінювання.

Спонтанне випромінювання елементарного об’єму середовища характеризується значенням кутової густини спонтанного об’єму випромінювання jn, яка дорівнює потоку енергії з частотою n, що випромінює одиничний об’єм за одиницю часу в межах одиничного тілесного кута у даному напрямку s,

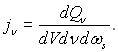(28.39)

Для ізотропного середовища за умови термодинамічної рівноваги випускання енергії не залежить від напрямку, тому можна множити величину jn на повний тілесний кут 4p, який оточує елементарний об’єм, отримуючи так названу спектральну об’ємну густину спонтанного випромінювання h_сn, яка представляє собою кількість енергії випромінювану з даною частотою, що випускає одиничний об’єм в одиницю часу за всіма напрямками:

(28.40)

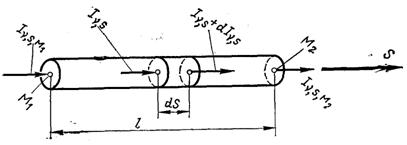
Рис.28.16. Послаблення інтенсивності падаючого випромінювання на шляху променя

Поглинуте і розсіяне випромінювання, яке проходить через об’єм у напрямку s (рис.28.16) і призводить до послаблення променя, виражається законом Бугера, згідно якому відносне зменшення інтенсивності падаючого випромінювання на безмежно малому шляху ds внаслідок його поглинання і розсіювання пропорційне шляху променя:

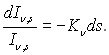(28.41)

Коефіцієнт Кn називається ефективним коефіцієнтом послаблення середовища і представляє собою суму коефіцієнтів ефективного поглинання a_n і розсіювання b_n:

Кn = a_n + b_n. (28.42)

Інтегрування (28.41) по напрямку s і довжині ℓ від точки М₁ до точки М₂ дає значення тієї частини інтенсивності випромінювання, що падає на об’єм у точці М₁, яка проходить не поглинутою до точки М₂:

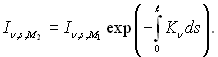(28.43)

Показник степеня в (28.43) називається спектральною оптичною довжиною променя у ослабленому середовищі:

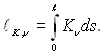(28.44)

Якщо радіаційні властивості середовища усталені в усьому об’ємі, то Кn = const і ℓ _К,n = Кnℓ  = ℓ n. У цьому випадку

(28.45)

Загальна кількість енергії з частотою n, яка приходить в об’єм зі всіх напрямків і поглинається в об’ємі, характеризується об’ємною спектральною густиною поглинутого випромінювання h_погn:

(28.46)

При термодинамічній рівновазі середовища і випромінюваної кількості енергії, яка поглинається об’ємом, повинно дорівнювати кількості енергії, випромінюваної ним. При цьому необхідно пам’ятати, що інтенсивність випромінювання у рівноважних умовах виражається законом Планка (28.1) і не залежить від напрямку. У цьому випадку інтегрування рівняння (28.46) приводить до залежності

(28.47)

Таким чином, об’ємна густина спонтанного випромінювання середовища може бути виражена через коефіцієнт ефективного поглинання середовища і інтенсивність випромінювання абсолютно чорного тіла:

(28.48)

Рівняння (28.48) виражає закон Кірхгофа для об’ємного випромінювання, і пов’язує між собою поглинальну і випромінювальну характеристики середовища.

У реальних умовах радіаційного теплообміну відсутня термодинамічна рівновага між речовиною і випромінюванням, при цьому речовина з надлишком чи отримує, чи віддає променеву енергію і h_погn № h_сn. За таких умов закон Кірхгофа уже не діє. Питання не рівноважного випромінювання дуже складні і ще недостатньо вивчені. Тому при розрахунках застосовується гіпотеза локальної термодинамічної рівноваги між елементарними частинками речовини у кожній точці об’єму, не дивлячись на відсутність рівноваги між речовиною і випромінюванням. При цьому радіаційні властивості речовини такі ж, як і при рівновазі при температурі, рівній температурі речовини у даній точці.

28.4.3. Перенесення енергії випромінювання у напівпрозорому середовищі

При переході від точки до точки інтенсивність випромінювання безперервно змінюється внаслідок одночасного проходження процесів поглинання (тобто перетворення променевої енергії в енергію хаотичного руху мікрочастинок середовища), випускання (тобто перетворення енергії теплового руху в енергію електромагнітного випромінювання) і розсіяння. У залежності від того, які з названих процесів переважають, може відбуватися як послаблення, так і підсилення інтенсивності випромінювання по ходу променя. Рівняння перенесення променевої енергії можна отримати шляхом складання балансу енергії випромінювання, яка знаходиться в частотному інтервалі від n до n + dn і розповсюджується в заданому напрямку s, для елементарного об’єму dV, розміщеного на шляху променя (рис.28.17).

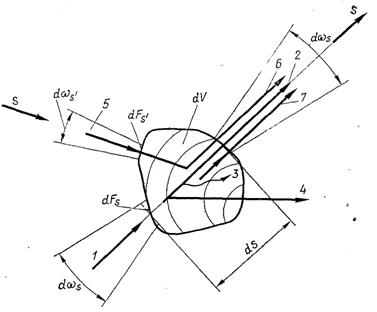
Рис.28.17. До балансу променевої енергії елементарного об’єму: 1 – потік випромінювання, що падає на об’єм у напрямку s; 2 – потік випромінювання, що пропускається у напрямку s;3 – частина падаючого випромінювання, що поглинається об’ємом dV; 4 – частина падаючого випромінювання, що розсіюється в об’ємі dV;5– потік випромінювання, що падає на об’єм dV у напрямку sў; 6 – частина падаючого випромінювання, що розсівається у напрямку s; 7 – власне (спонтанне) випромінювання об’єму у напрямку s

Шуканою величиною є зміна кількості енергії випромінювання між виходом з елементарного об’єму і входом до нього (у напрямку s). Спочатку запишемо баланс енергії, називаючи кожний із членів, що входить до балансу:

Ліва частина рівняння балансу представляє собою зміну інтенсивності випромінювання:

де dℓ n_,s – зміна на шляху ds інтенсивності випромінювання, яка характеризується частотою n ; dF_s – площа основи елементарного циліндра, перпендикулярного до напрямку s; dw_s – елементарний тілесний кут навколо напрямку s.

Послаблення пучка за рахунок ефективного (тобто, що враховує як дійсне поглинання, так і індуковане випускання) поглинання і розсіювання пропорційне інтенсивності випромінювання у відповідності із законом Бугера (28.41):

Підсилення пучка внаслідок спонтанного випромінювання пропорційне об’ємній густині спонтанного випромінювання h_сn, величині елементарного об’єму dV і величині елементарного тілесного кута dw_s. Враховуючи, що спонтанне випромінювання розподіляється рівномірно у просторі по повному (сферичному) тілесному куту 4p, можна записати

Використовуючи закон Кірхгофа (48.48), можна виразити цю величину через спектральну інтенсивність абсолютно чорного випромінювання І_0,n при температурі середовища у розглядуваній точці і через ефективний спектральний коефіцієнт поглинання a_n:

Підсилення пучка за рахунок розсіювання у напрямку s виражається наступним чином. З довільного напрямку sў у межах елементарного тілесного кута dw_s, в об’єм dV надходить потік променевої енергії Іn_,sў dF_sў dw_sў , де dF_sў – проекція міделя елементарного об’єму на площину, перпендикулярну sў. З цієї кількості енергії розсіюється у напрямку sў її частина, пропорційна шляху dsў, коефіцієнту розсіювання b_n і індикатрисі розсіювання g_n(s, sў), тобто Проінтегруємо цей вираз по всім напрямкам sў (тобто у межах повного сферичного кута 4p, звідки на об’єм dV падає променева енергія), отримуємо шукану величину:

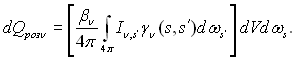
При цьому враховується, що dF_sў dsў = dV і що значення b_n, dw_s і dV не залежать від напрямку sў.

Додаємо (з відповідними знаками) отримані вирази:

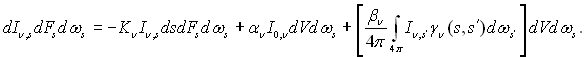
Розділимо всі члени на dF_sdsdw_s отримаємо рівняння переносу енергії випромінювання у напівпрозорому середовищі розсіву:

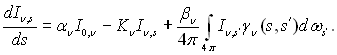(28.49)

Гранична умова до рівняння (28.49) задається у вигляді зв'язку значень інтенсивності випромінювання у точках N граничної поверхні з радіаційними характеристиками поверхні. Можна, наприклад, записати інтенсивність ефективного випромінювання поверхні як інтенсивність випромінювання Іn_,–п, що розповсюджується у напрямку внутрішньої нормалі до поверхні (–п = s), і прирівняти цю величину до суми власного випромінювання поверхні до відбитого від неї випромінювання. При цьому відбите випромінювання виражається через падаюче випромінювання, тобто через інтенсивність випромінювання Іn_,+п, яке надходить до точки N поверхні зі всіх напрямків sў у межах півсфери з боку випромінюючого об’єму. У випадку дифузійної випромінюючої і відбиваючої поверхні граничні умови виражаються рівнянням

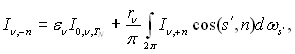(28.50)

де Іn_,–п = І_ст.еф,n – інтенсивність ефективного випромінювання поверхні стінки; e_n і rn – спектральна ступінь чорноти і відбивна спроможність поверхні; – інтенсивність рівноважного випромінювання при температурі поверхні стінки у точці N.

Рівняння переносу і гранична умова до нього є дуже складними, навіть при зроблених допущеннях і передбаченнях. Наявність розсіювання призводить до того, що рівняння розповсюдження енергії є інтегродиференціальним, а об’ємний характер процесу випромінювання примушує граничну умову (28.50) записувати у вигляді інтегрального рівняння. Для практичного використання, наприклад для знаходження ефективного променевого потоку від елементу поверхні в районі точки N, ці рівняння необхідно сумісно інтегрувати як по довжині, так і по напрямку кожного променя, який виходить з точки N у бік напівпрозорого об’єму. Аналітичне рішення цих рівнянь у загальному випадку неможливе. Навіть при використанні наближених (включаючи і машинні числові методи) рішень приходиться робити багато додаткових спрощень стосовно геометрії системи, радіаційних властивостей середовища і поверхонь, розподілу температури та ін. Особливо великі труднощі виникають при розрахунку випромінювання газів пов’язані зі смушковою структурою спектрів їх випромінювання і різкою залежністю радіаційних характеристик газів від частоти випромінювання і температури.