28.2.4. Закон Ламберта (закон косинуса)

Цей закон дозволяє відповісти на питання про кількісну оцінку радіації у фіксованому напрямку, коли випромінювання поверхні у на півсферу носить дифузійний характер і рівномірно розподілене в об’ємі. Повна енергія випромінювання, яка дифузійно віддається елементом поверхні dF, можна визначити як

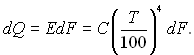(28.16)

Закон Ламберта стверджує, що кількість променевої енергії, яка передається у напрямку j від нормалі до елементу dF, пропорційна величині просторового кута, до якого відбувається випромінювання dW, і cosj (рис.28.6), тобто

(28.17)

де Е_п –енергія випромінювання у напрямку нормалі до dF.

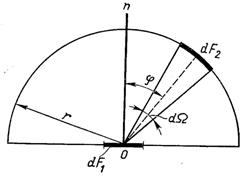
Рис.28.6. До виводу закону Ламберта

Знаходимо співвідношення між Е і Е_п. Тілесний кут визначається за аналогією із плоским. Для плоского кута

dj = ds/r,

де ds – дуга, на яку спирається плоский кут.

Для тілесного кута

dW = dF/r².

Координуючи довготу через y (рис.28.7), а через j – полярну відстань, тобто

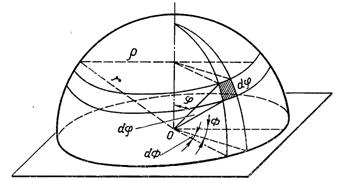
Рис.28.7. До визначення просторового кута у сферичних координатах

90° мінус широта, перейдемо до безмежно малого сферичного прямокутника dF₁, сторона якого rdj і rdy = rsinjdy, тоді dW = = dF₁/r² = sinjdjdy. Підставимо значення тілесного кута в (28.17), отримаємо:

dQ = E_nsinjcosjdjdydF.

Для півсфери

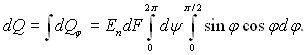
Але cosjdj = d(sinj), то

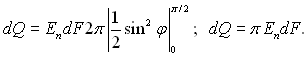
Порівнюючи отримані результати з (28.16), видно, що

(28.18)

Ця залежність говорить про те, що променевий потік у напрямку нормалі у p разів менший за дифузійне випромінювання у півсферу.

Кількість енергії, яка віддається у напрямку j від нормалі тепер можна виразити наступним чином:

(28.19)

чи

де dw – тілесний кут, який спирається на елементарну площадку, e_j = Еj/Е_0j.

Закон Ламберта строго справедливий тільки для абсолютно чорного тіла. Якщо для сірої поверхні випромінювання підпорядковується закону Ламберта, то ступінь чорноти не залежить від кута j і e_j = e_п = e.

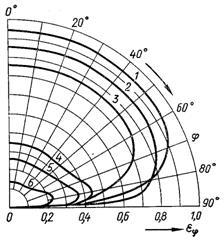
Рис.28.8. Відхилення від закону Ламберта: 1 – дерево; 2 – корунд; 3 – окислена мідь; 4 – вісмут; 5 – алюмінієва бронза; 6 – латунь

У діелектриків, окислених поверхонь металів значне відхилення від закону Ламберта спостерігається при j > 60° (рис.28.8). У полірованих металевих поверхонь відхилення від закону Ламберта більш суттєве. Закон Ламберта справедливий і для монохроматичного випромінювання.

Закони Планка, Стефана – Больцмана, Ламберта строго справедливі для випромінювання абсолютно чорного тіла, для випромінювання, яке містить у собі невелику кількість енергії можливої при даній температурі. Це можна показати за допомогою закону Кірхгофа.

28.2.5. Закон Кірхгофа

Цей закон виявляє зв’язок між випромінюваною і поглинальною здатністю тіла.

Розглянемо променевий теплообмін між двома поверхнями, розташованими так, що випромінювання одної з них обов’язково потрапляє на

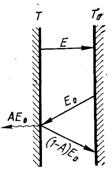
Рис.28.9. До виводу закону Кірхгофа

іншу без втрат (рис.28.9). Вважаємо, що одна поверхня є абсолютно чорною з температурою Т₀, інша – сіра з поглинальною здатністю А і температурою Т.

Поки Т > T₀ між поверхнями відбувається променевий теплообмін так, що

q = E – AE₀,

де Е – енергія випромінювання сірого тіла, яка повністю поглинається чорним; Е₀ – енергія випромінювання чорного тіла, яка частково поглинається сірим (АЕ₀). Залишок, відбиваючись від сірого тіла, поглинається чорним.

Коли температура тіл зрівнюється, теплообмін буде продовжуватися, але з нульовим ефектом (у випадку конвекції чи теплопровідності перенос теплоти за таких умов припиняється):

q = 0; E = AE₀,

чи

Е/А = Е₀. (28.20)

Отриманий результат можна розповсюдити на довільну кількість тіл:

Е₁/А₁ = Е₂/А₂ = ... = Е₀. (28.21)

Відношення енергії випромінювання тіла до його поглинальної здатності для всіх тіл однаковий і рівний енергії випромінювання абсолютно чорного тіла при тій же температурі. Це відношення є функцією тільки температури.

Тому що

Е = es₀Т⁴,

то на підставі (28.21)

es₀Т⁴/А = s₀Т⁴,

чи

e = А. (28.22)

Отже, ступінь чорноти тіла чисельно дорівнює його поглинальній здатності в умовах термодинамічної рівноваги. Звідси можна зробити висновок, що для всіх тіл, крім чорного, енергія випромінювання сірих тіл менша енергії випромінювання чорного тіла. Таким чином, при любій температурі енергія випромінювання абсолютно чорного тіла є найбільшою. Тіла з малою поглинальною здатністю мають малу випромінювану спроможність, і навпаки. Тому стінки балонів термосів і посудин Дюара для покращення ізоляційних властивостей покривають алюмінієвою чи срібною амальгамою (для срібла e = 0,02...0,03, для полірованого алюмінію e = 0,04...0,06).

Вираз (28.21) закону Кірхгофа справедливий для інтегрального випромінювання. Однак, закон можна розповсюдити і на монохроматичне випромінювання:

Е_1l/А_1l = Е_2l/А_2l = ... = Е_0l. (28.23)

тобто відношення енергії випромінювання тіла при фіксованій довжині хвилі до його поглинальної спроможності при тій же довжині хвилі і при тій же температурі однакове для всіх тіл і залежить тільки від довжини хвилі і температури.

Необхідно зауважити, що закон Кірхгофа отриманий для умов температурної рівноваги, коли температури випромінювача і приймача однакові, і справедливий тільки для цього випадку

Вище було сказано, що поняття абсолютно чорного тіла відіграє значну роль як в теорії променевого теплообміну, так і в технічних додатках. Прикладами можуть служити температури яскравості, радіації і кольоровості. Функціональні зв’язки цих понять з температурою випромінювання, отримані на підставі законів випромінювання абсолютно чорного тіла, лежать в основі оптичних методів вимірювання високих температур.

Температурою яскравості називається температура абсолютно чорного тіла, за якої його спектральна інтенсивність випромінювання для певної довжини хвилі дорівнює спектральній інтенсивності випромінювання даного тіла для тої ж довжини хвилі. За визначенням Іl = І^я_0l. Використовуючи (28.10), визначимо інтенсивність випромінювання тіла, нагрітого до температури Т:

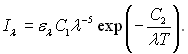
Щоб абсолютно чорне тіло мало ту ж інтенсивність випромінювання, його необхідно нагріти до температури Т_я:

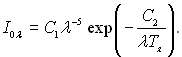
Прирівнюючи праві частини двох останніх рівнянь і виконавши необхідні перетворення, отримаємо

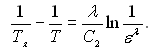
Чим менша ступінь чорноти (e_l) тим більша різниця між дійсною температурою і температурою яскравості, при цьому, оскільки 0 < e_l < 1, то температура яскравості Т_я завжди менша дійсної Т.

Радіаційною називається така умовна температура, яку повинно мати тіло, щоб її випромінювання було чорним. Отже, на підставі (28.12) можна написати

чи

Кольоровою температурою називають температуру абсолютно чорного тіла, за якої розподіл його спектральної інтенсивності і інтенсивності випромінювання даного тіла практично співпадають з видимою ділянкою спектра. Для визначення кольорової температури використовують монохроматичне випромінювання тіла, яке відповідає двом різним довжинам хвиль при температурі Т. Це співвідношення повинно бути таким же і для абсолютно чорного тіла при тих же довжинах хвиль, але вже при температурі Т_к. Тоді

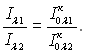
Підставляючи значення І з (28.10) , отримаємо залежність:

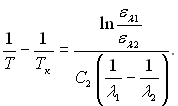
Кольорова температура Т_к завжди трохи більша за дійсну Т.

28.3. Радіаційний теплообмін між тілами, розділеними діатермічним (прозорим) середовищем

28.3.1. Теплообмін між двома паралельними пластинами

Визначимо кількість теплоти, якою обмінюються два тіла, поверхні яких паралельні між собою. Нехай довжини хвиль випромінювання обох тіл в одній спектральній області. При цьому відстань між тілами така, що промінь, який виходить з одного тіла, обов’язково потрапляє на друге, а величина кожної з поверхонь дуже велика. Іншими словами, втратами променевої енергії нехтуємо. Крім цього, для кожного тіла записати

А + R = 1; D = 0.

Температури тіл неоднакові Т₁ № Т₂.

Рис.28.10. Радіаційний теплообмін між паралельними пластинами

Розглянемо, що відбувається з енергією, яка випромінюється тілом 1 (рис.28.10). Тіло 1 випромінює Е₁, а тіло 2 поглинає Е₁А₂ і відбиває Е₁R₂. З того, що відбило тіло 2, тіло 1 сприйняло Е₁R₂А₁ і відбило Е₁R₁R₂. З цієї кількості енергії тіло 2 поглинає Е₁R₁R₂А₂ і відбиває Е₁R₁R₂². У свою чергу тіло 1 поглинає звідси Е₁R₁R₂²А₁ і відбиваєЕ₁R₁²R₂² і т. д.

Точно такі ж міркування провести і для енергії, випромінюваної тілом 2. Для цього достатньо поміняти місцями індекси у попередніх викладках: тіло 2 випромінює Е₂, звідки тіло 1 поглинає Е₂А₁ і відбиває Е₂R₁. З цього випромінювання тіло 2 поглинає Е₂R₁А₁, а відбиває Е₂R₁R₂ і т. д.

Вважаємо, що температура поверхні тіла 1 вища: Т₁ > Т₂. Тоді результуючий потік променевої енергії спрямований у бік другого тіла 2, який буде приймачем радіації, а 1 – випромінювачем. Для того щоб знайти енергію, яку отримує приймач внаслідок взаємного обміну, необхідно побудувати тепловий баланс. Тіло 2 отримує частку енергії від випромінюваної тілом 1, частину енергії власного випромінювання, відбиту тілом 1 і знову поглинуто поверхнею приймача, мінус власне випромінювання. Тоді

Q = Q₁ + Q₀² – Q₂.

Визначимо кількість енергії, випромінювану тілом 1, яка поглинається тілом 2:

Q₁ = F(Е₁А₂ + Е₁R₁R₂А₂ + Е₁A₂R₁²R₂² +...),

чи

Q₁ = FЕ₁А₂(1 +R₁R₂ +R₁²R₂² +...).

Якщо R₁R₂ = р < 1, то сума членів безмежно спадної геометричної прогресії буде:

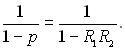
Тоді

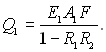
Кількість енергії з власного випромінювання тіла 2, яке повернулося до нього і знову поглинуте ним, складає

чи

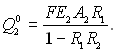
Кількість енергії, що випромінюється тілом 2:

Q₂ = FЕ₂.

Загальне надходження енергії у балансі тіла 2:

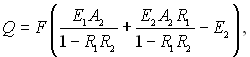
чи

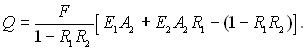
Але А₂ = (1 – R₂), тоді

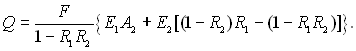(28.24)

Відкриємо в правій частині квадратні дужки:

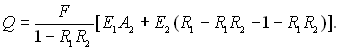
Маючи на увазі, що (1 – R₁) = А₁, після нескладних перетворень отримаємо

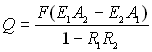. (28.25)

Розкриємо знаменник правої частини отриманого рівняння:

1 – R₁R₂ = 1 – (1 – A₁)(1 – A₂) = A₁ + A₂ – A₁A₂,

але тому що

e = А₁; С =eС₀; А₁ = С₁/С₀; А₂ = С₂/С₀,

то

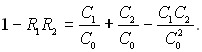
Ураховуючи значення

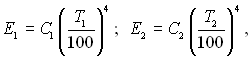
повернемося до співвідношення (28.25):

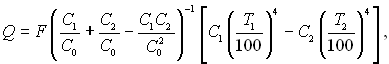
чи

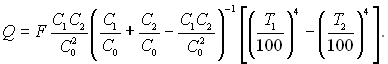
Розділимо чисельник і знаменник на С₁С₂/С₀, отримаємо

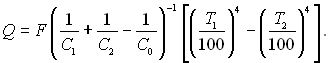
Другий співмножник у правій частині називають приведеним коефіцієнтом випромінювання С_пр

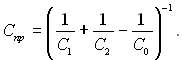
Тоді у кінцевому вигляді отримаємо формулу:

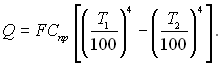(28.26)

У приведений коефіцієнт випромінювання окрім коефіцієнтів випромінювання випромінювача і приймача входить також коефіцієнт випромінювання абсолютно чорного тіла. Якщо і випромінювач і приймач – абсолютно чорні тіла, то величина С буде найбільшою. Якщо тільки одне з тіл буде абсолютно чорним, то приведений коефіцієнт випромінювання буде дорівнювати коефіцієнту випромінювання сірого тіла.

Тому що С/С₀ = e, то приведений коефіцієнт випромінювання можна замінити приведеним ступенем чорноти

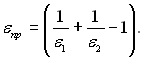
У цьому разі вираз (28.26) набуває наступного вигляду:

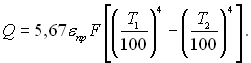
У технічних розрахунках зазвичай використовують поняття приведеного ступеня чорноти.

28.3.2. Радіаційний теплообмін між тілом і оболонкою

Розглянемо променевий теплообмін між двома тілами, коли одне з них повністю охоплене іншим (рис.28.11), при цьому як форма обох тіл, так і положення 1 всередині оболонки не обмежені. Висувається тільки одна умова до тіла 1, воно повинне бути скрізь опуклим (воно не може випромінювати само на себе), поверхня оболонки – в усіх точках ввігнута.

Рис.28.11. Радіаційний теплообмін між тілом і оболонкою

Для обох тіл A + R = 1, випромінювання дифузійне, температури тіл різні. При цьому хід міркувань буде таким самим як і в попередній задачі. Необхідно тільки урахувати наступну обставину: з енергії, відбитої оболонкою, перше тіло сприймає тільки частину bЕ₁R₂, а залишок, рівний (1 – b)Е₁R₂, проходить біля нього і знову потрапляє на поверхню оболонки. Тоді для цього випадку можна записати такий вираз, використовуючи умови попередньої задачі:

1 – (1 – А₁)(1 – А₂) = А₁ + А₂ – А₁А₂,

звідки

1 – (1 – bА₁)(1 – А₂) = bА₁ + А₂ – bА₁А₂. (28.27)

З рівняння (28.25) отримуємо як кількість теплоти, поглинутої оболонкою при випромінюванні першого тіла [з урахуванням виразу (28.27)]:

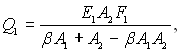
так і кількість теплоти, випроміненої оболонкою і поглинутою тілом 1:

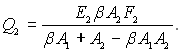
Тепер для визначення b тимчасово приймемо, що Т₁ = Т₂, тоді Q₁ = Q₂ і F₁ = bF₂, чи b = F₁/F₂. Кількість теплоти, якою у дійсності обмінюються тіла 1 і 2 при Т₁ № Т₂, визначається так:

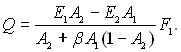(28.28)

Враховуючи, що

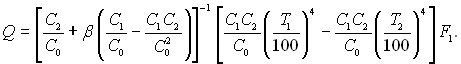
Після перетворення

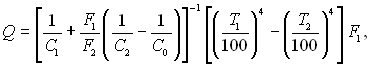
чи

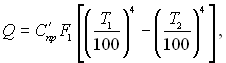
де

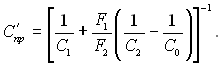
Як і в попередній задачі, приведений коефіцієнт випромінювання можна замінити на приведену ступень чорноти:

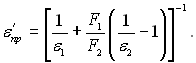
І в кінцевому вигляді

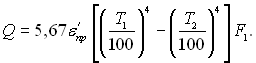(28.29)

Слід зауважити, якщо F₂ >> F₁, то Сў_пр = С₁, а eў = e₁.

28.3.3. Захисні екрани

Оскільки випромінювання визначається температурою, то кількість радіаційної енергії можна регулювати, впливаючи на температуру випромінювача. Часто трапляються випадки, коли неможна зменшити цю температуру для того, щоб зменшити дію променевого потоку. У цих випадках застосовують екрани. Екрани для захисту від теплового випромінювання виконують з металів з великою відбивною і малою поглинальною спроможністю.

Уявимо, що між двома великими плоскими паралельними поверхнями 1 і 2 знаходиться екран Е з такого тонкого матеріалу, що різницею температур між його поверхнями можна знехтувати. Вважаємо, що можна знехтувати конвективним переносом теплоти між поверхнями випромінювання. Знайдемо спочатку кількість теплоти q₀ якою обмінюються поверхні без екрану, а далі кількістю теплоти q₁, якою вони обмінюються після установки екрану.

Розглянемо два випадки.

1. Поверхні тіл 1 і 2, як і обидві поверхні екрану мають однаковий коефіцієнт випромінювання С₁. Тоді приведений коефіцієнт випромінювання системи можна представити у вигляді наступного рівняння: 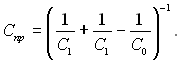Результуючий потік теплоти від тіла 1 на тіло 2 без екрану буде

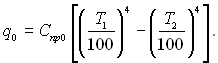
Коли між тілами 1 і 2 знаходиться екран, результуючий тепловий потік можна представити як

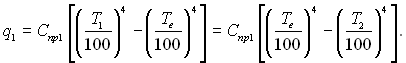
З останнього рівняння виходить, що

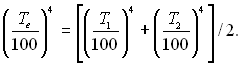
Підставимо отриману величину у вираз для q₁:

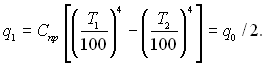
Отже, завдяки підключенню одного екрану тепловий потік на тіло 2 зменшується вдвічі.

Отриманий розв’язок можна розповсюдити на випадок 2, 3,..., п екранів:

(28.30)

Таким чином при наявності п екранів результуючий тепловий потік на приймач зменшиться в (п – 1) разів.

2. Розглянемо випадок, коли коефіцієнт випромінювання обох поверхонь тіл рівний, як і в попередньому випадку С₁, а коефіцієнт випромінювання поверхні екрану становить С_е.

Тоді при відсутності екрану запишемо приведений коефіцієнт випромінювання системи двох тіл

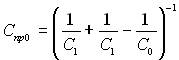
і результуючий тепловий потік від тіла 1 до тіла 2

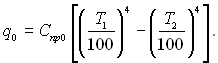
Введений в систему екран змінить приведений коефіцієнт випромінювання системи:

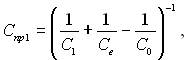
а тепловий променевий потік між тілами і екраном

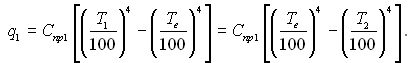
Температура екрану, як і в першому випадку, буде

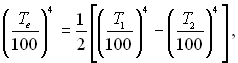
а тепловий потік

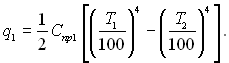
Таким чином,

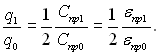(28.31)

Отже результуючий тепловий потік залежить не тільки від кількості екранів, як було показано вище, але і від співвідношення між оптичними властивостями випромінюючих поверхонь і екрану. Останнє кількісно визначається співвідношенням приведених поглинальних спроможностей (ступеня чорноти) джерела і приймача випромінювання до приведеної поглинальної спроможності (ступеня чорноти) екрану.

Відстань до екрану від випромінювальних поверхонь для визначення променевого теплообміну значення не має. Для розрахунку повного теплового потоку необхідно враховувати як перенос теплоти теплопровідністю, так і конвективний теплообмін у середовищі, яке заповнює об’єм між екраном і випромінюваним джерелом.

28.3.4. Радіаційний теплообмін між довільними поверхнями нагріву

Тіла, які обмінюються променевим теплом, розташовані у просторі одне відносно іншого довільно. У цьому випадку можна виділити на поверхні кожного тіла декілька характерних елементів і розглянути теплову взаємодію між ними

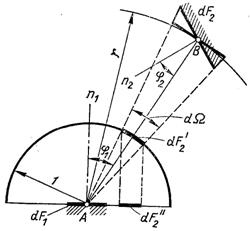
Рис.28.12. До виведення формули для кутового коефіцієнту

Нехай dF₁ і dF₂ – довільно розташовані у просторі елементи поверхні з температурами відповідно Т₁ і Т₂ (рис.28.12). Поглинальна спроможність цих елементів А₁ і А₂, коефіцієнти випромінювання С₁ = e₁С₀ = А₁С₀ і С₂ = e₂С₀ = А₂С₀. Відстані між центрами елементів r і нормалями до площин елементів j₁ і j₂.

Тепер кут бачення dF₁ із dF₂

Дифузійне випромінювання енергії елементом dF₁ на dF₂ можна визначити, використовуючи закон Ламберта (28.19):

чи

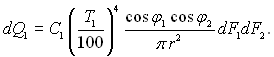(28.32)

Енергія поглинута другим елементом,

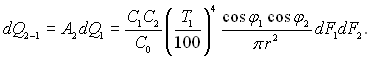
Вважаючи, що ступінь чорноти елементів поверхні висока, енергію випромінювання другого тіла на перше, поглинуту ним, знайдемо так:

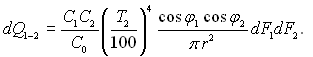
Таким чином, кількість теплоти, якою обмінюються елементи поверхні,

чи

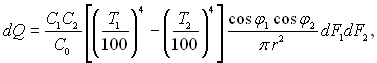
звідки

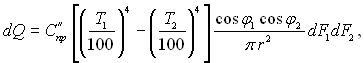(28.33)

де СІ_пр = С₁С₂/С₀.

Проінтегруємо вираз (28.33) по F₁ і F₂:

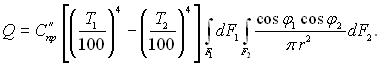(28.34)

Найбільшу складність при рішенні цього рівняння становить визначення комплекса:

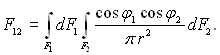(28.35)

Цей комплекс має розмірність площі і називається взаємною поверхнею випромінювання. Отже, задача розрахунку променевого теплообміну між двома тілами, довільно розташованими у просторі, за своєю суттю зводиться до знаходження значення взаємної поверхні випромінювання F₁₂. Відношення потоку випромінювання від поверхні одного тіла на поверхню другого тіла до повного потоку власного випромінювання, яке виходить з усієї поверхні першого тіла по різних напрямкам у межах півсферичного тілесного кута, називається середнім кутовим коефіцієнтом випромінювання чи коефіцієнтом опроміненості і позначається j_ik. За визначенням для двох поверхонь нагріву:

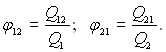(38.36)

Якщо повний променевий тепловий потік від тіла 1 можна подати як

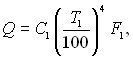
а потік випромінювання тіла 1 на поверхню тіла 2 з (28.32), як

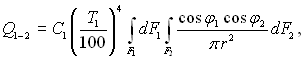
то із співвідношення (28.36) отримаємо j₁₂ = F₁₂/F₁ і аналогічно j₂₁ = F₁₂/F₂. Ці два рівняння установлюють взаємозв’язок між кутовими коефіцієнтами:

j₁₂F₁ = j₂₁F₂. (28.37)

Це рівняння справедливе за умови, що радіаційні потоки від поверхонь, які приймають участь у теплообміні, є дифузійними. Величини потоків не змінюються на відповідних поверхнях.

Коли розглядається теплообмін випромінюванням у системі з п поверхонь, то для кожної пари поверхонь можна записати

j_ikF_i = j_kiF_k,

де і = 1, 2, 3,..., п; k = 1, 2, 3,..., п.

У випадку, коли поверхня тіла має ввігнутість, можливе само опромінювання (і = k), тоді

j_iі = Q_ii /Q_i.

Якщо тіла утворюють замкнену систему, то

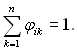
Ця сума включає в себе і члени j_iі.

Радіаційні теплові потоки, які направляють поверхні одних ті на другі, можна визначати, використовуючи поняття кутових коефіцієнтів:

Q_ik = j_ikQ_i.