Частина п’ята. ТЕПЛОВЕ ВИПРОМІНЮВАННЯ

     Розділ 28. ПРОМЕНЕВИЙ ТЕПЛООБМІН

Процеси теплопередачі можна розділити на дві категорії. Перша визначається тим, що структурні елементи середовища, які знаходяться на шляху переносу теплоти, приймають участь у процесі переносу. Це теплопровідність і конвекція. Друга категорія характеризується тим, що середовище може не приймати участі в перенесенні теплоти. Це теплове випромінювання. Таким чином, між процесами теплопровідності і конвекції, з одного боку, і тепловим випромінюванням – з іншого, існує принципова різниця.

Конвективний перенос теплоти і теплопровідність розглядалися при безперервному температурному полі і у тих випадках, коли теплота переходить від твердого тіла до рідини і навпаки. Температурний градієнт завжди мав кінцеве значення, крім тих випадків коли дорівнював нулю.

Теплове випромінювання – складний процес, пов’язаний з тим, що під по крайній мірі двічі відбувається перетворення енергії: спочатку перехід теплової енергії у випромінювання (перше перетворення енергії) електромагнітних хвиль (емісія), далі рух хвиль (фотонів) і, на кінець, поглинання електромагнітних коливань поглинаючим середовищем чи тілом (абсорбція) – друге перетворення енергії.

Теплове випромінювання розглядається як процес розповсюдження поперечних електромагнітних хвиль, які надходять від випромінювача. Ці електромагнітні хвилі розповсюджуються прямолінійно і при поглинанні їх будь яким тілом чи середовищем знову перетворюються в теплоту.

Характеризуються електромагнітні коливання довжиною хвилі l і частотою n, які зв’язані між собою залежністю

ln = с, (28.1)

де с = 2,998·10⁸ м/с – швидкість світла у вакуумі.

Носіями теплової променевої енергії – є електромагнітні хвилі, які відрізняються між собою тільки своєю довжиною. Дія випромінювання при падінні його на речовину залежить від довжини хвилі. Наближена класифікація різного виду випромінювання може бути такою (за довжиною хвиль, м):

космічне випромінювання.............до 10^–13

g- випромінювання.........................10^–13...10^–10

рентгенівські промені....................5·10^–12...2·10^–8

ультрафіолетові промені...............2·10^–8...4·10^–7

видимі (світлові) промені.............4·10^–7...8·10^–7

теплові промені.............................10^–7...10^–4

радіохвилі......................................> 2·10^–4

Більша частина довжин хвиль, що відповідає тепловому випромінюванню, не співпадає з довжиною хвиль світлових променів. Випромінювання, яке визначається термічним діапазоном довжин хвиль називається інфрачервоним, при цьому інфрачервоне випромінювання може містити у собі весь спектр довжин хвиль, характерних для нього, у цьому разі воно називається інтегральним. Але теплове випромінювання може відбуватися в межах незначної ділянки виділеного спектру довжин хвиль, у цьому разі воно називається спектральним.

Природа теплових і видимих (світлових) променів однакова, то і їх фізичні властивості в основному одні і ті самі. Закони розповсюдження, відбиття і заломлення, які установлені для видимого проміння, справедливі і для теплових променів.

Випромінювати промені властиво всім тілам і кожне з них випромінює енергію безперервно, при цьому випромінюють як гарячі тіла в системі, так і холодні. Кількість променевої енергії, яка виникає в тілі, визначається температурою і залежить тільки від неї.

28.1. Основні поняття і визначення

Коли потік випромінювання Q із навколишнього середовища потрапляє на деяке тіло (рис.28.1), то у загальному випадку частина цього потоку Q_R відбивається від тіла, частина енергії Q_A поглинається тілом і частина Q_D проходить крізь тіло. Таким чином, згідно закону збереження енергії,

Q = Q_R + Q_A + Q_D. (28.2)

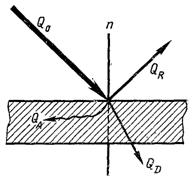
Рис.28.1. Схема розподілу променевого потоку, що потрапляє на довільне тіло

Якщо кут падіння дорівнює куту відбиття і відбитий промінь зберігає свою форму, то відбиття називається дзеркальним. Коли при відбитті падаючий промінь перетворюється в пучок променів, рівномірно розподілених у півпросторі, то відбиття називається дифузійним. Поверхня, яка створює таке відбиття називають матовою, а поверхня, яка дає дзеркальне відбиття – блискучою.

Відношення потоку випромінювання відбитого поверхнею тіла (середовища) до потоку випромінювання, що падає на поверхню, називають відбивною здатністю і позначають R = Q_R / Q.

Не відбита частина енергії може частково пройти через тіло без зміни, а частина її може поглинатися тілом і перетворюватися в теплоту. І пропускання і поглинання залежать від фізичних властивостей і форми тіла, від довжини хвилі за якою відбувається випромінювання. Метали, наприклад, непроникливі для різних видів випромінювання. Але можна виготовити настільки тонку металеву фольгу, яка буде пропускати світлові проміння; рентгенівське випромінювання спроможне проникати через металеві пластини товщиною в декілька десятків міліметрів. Кварц не пропускає теплове випромінювання, а для світлових і ультрафіолетових променів прозорий. Кам’яна сіль, навпаки, непрозора для ультрафіолетових променів і пропускає теплові. Звичайне віконне скло світлові промені пропускає, а ультрафіолетові – ні.

Відношення потоку випромінювання, що поглинається тілом (середовищем), до потоку випромінювання, що падає на тіло (середовище) називається поглинальною здатністю і позначають як А = Q_A / Q.

Відношення потоку випромінювання, що пропускається тілом (середовищем), до потоку випромінювання, що падає на тіло (середовище) називається пропускною спроможністю і позначається як D = Q_D / Q.

За цих умов, з урахуванням рівняння (28.2)

R + A + D = 1. (28.3)

Розглянемо окремі випадки цього виразу. Очевидно, що величини R, A і D визначаються властивостями тіла, яке приймає потік випромінювання. Як тверді, так і рідкі тіла поглинають у дуже тонкому шарі майже все теплове випромінювання, яке надходить до їх поверхні. Для металів товщина цього шару становить приблизно один мікрометр, для більшості інших тіл – біля 1,3 мм. Таким чином, у першому наближенні для рідких і твердих тіл можна говорити про поглинальну поверхню, а рівняння (28.3) спростити до вигляду:

R + A = 1.

Тіла, які підпорядковуються цій залежності, називають сірими тілами. Для них спектральна поглинальна спроможність не залежить від довжини хвилі (частоти) падаючого проміння.

Дослідно установлено, що гази майже не відбивають випромінювання, які потрапляють на поверхню, що відокремлює їх від інших середовищ. У той же час навіть при значній товщині шару газ пропускає помітну кількість інфрачервоного випромінювання. Том вираз (28.3) можна представити так:

R + D = 1.

Необхідно розглянути і граничні види рівнянь (28.3):

R = A = 0, D = 1, A = D = 0, R = 1, R = D = 0, A = 1.

Ці рівняння відповідають так званим “абсолютним” тілам.

В першому випадку (D = 1) тіло називається абсолютно прозорим чи діатермічним. Воно повністю пропускає падаючі на нього випромінювання. Прикладом діатермічного середовища можуть служити двоатомні гази при помірних температурах.

В другому випадку (R = 1) тіло називається абсолютно білим чи дзеркальним. Поверхня такого тіла повністю відбиває усі падаючі на нього промені.

Останній випадок (A = 1) такий, коли тіло, поглинає падаючі на нього промені незалежно від напрямку падаючого випромінювання, його спектрального складу і поляризації, нічого не відбиває і не пропускає.

У природі не існує не абсолютно чорного, ні діатермічного, ні абсолютно білого тіла. Але ці поняття, особливо поняття абсолютно чорного тіла, відіграють значну роль в теорії випромінювання і широкого використання в інженерних розрахунках променевого теплообміну. Поверхні, які поглинають усі світлові промені, сприймаються оком як чорні. Однак поверхня може відбивати майже всі світлові промені і все ж сприйматися нами як абсолютно чорні, якщо вона не поглинає теплові випромінювання. З цієї точки зору свіже побілена стінка є майже чорною.

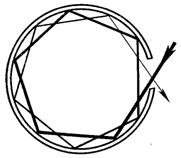
Рис.28.2. Модель абсолютно чорного тіла

З певною ступеню точності абсолютно чорне тіло можна відтворити повністю покриту сажею матову поверхню. Моделлю абсолютно чорного тіла може служити також порожниста сфера з невеликим отвором (рис.28.2), стінки якої мають велику поглинальну спроможність і зберігають усталеність температури. Промінь, який входить через отвір при багаторазовому відбиванні і поглинанні майже повністю губить свою енергію, віддаючи її стінкам сфери.

Потік випромінювання, який проходить через одиницю поверхні різними напрямками у межах напівсферичного тілесного кута, називається поверхневою густиною потоку випромінювання:

(28.4)

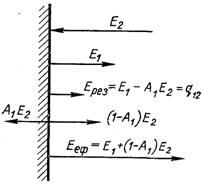
Рис.28.3. До визначення видів теплового випромінювання

Якщо оточуючі тіла мають температуру рівну нулю, то Е – вся енергія, яка випромінюється тілом. Коли температура хоч одного з оточуючих тіл відмінна від нуля, можна говорити про ефективне випромінювання, яке визначається як сума потоків власного і відбитого випромінювання (рис.28.3):

Е_еф = Е₁ + (1 – Е₁)Е₂. (28.5)

Фізичні властивості власного і відбитого випромінювання різні, оскільки падаючий променевий потік визначається температурами і властивостями обмежуючих тіл, але для енергетичної сторони процесу, для теплових розрахунків, ця різниця значення не має.

Випромінювана одиничною поверхнею енергія розподіляється в на півпросторі. Відношення густини потоку випромінювання, взяте у безмежно малому інтервалі для хвиль (частот), яке включає в себе дану довжину хвилі (частоти), до цього інтервалу, називається інтенсивністю випромінювання:

(28.6)

Природні джерела радіації одночасно випромінюють електромагнітні хвилі різної довжини. Але нерідко виникає необхідність розгляду променевого потоку, який характеризується одною довжиною хвилі. Випромінювання, яке відповідає достатньо вузькому інтервалу частот (довжин хвиль), які можна характеризувати даним значенням частоти (довжини хвилі), називається монохроматичним (однокольоровим).

28.2. Закони теплового випромінювання

Спектри випромінювання реальних твердих тіл на стільки різні, що описати їх єдиною аналітичною залежністю неможливо. У той же час абсолютно чорне тіло повністю поглинає всі падаючі на нього випромінювання, спектр розподілу енергії випромінювання такого тіла універсальний. У зв'язку з цим розрахунковим підґрунтям теплової радіації є закони випромінювання абсолютно чорного тіла.

28.2.1. Закон Планка

Енергія, випромінювана тілом, однозначно визначається його температурою. Але розподіл енергії за довжиною хвиль відбувається нерівномірно. Крім цього, випромінювання енергії дискретне, воно здійснюється окремими порціями – квантами.

Ще в 1900 р. М. Планк опублікував закон розподілу інтенсивності за довжиною хвиль при різних температурах

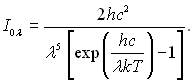(28.7)

де h = 6,625·10^–34 Дж/с – стала Планка; k = 1,380·10^–23 Дж/К – стала Больцмана; l – довжина хвилі, м; с = 2,998·10⁸ м/с – швидкість світла у вакуумі; Т – температура, К; всі величини, які стосуються абсолютно чорного тіла, позначаються підстрочним індексом “0”. Усі константи в рівнянні (28.7) об’єднують у комплекси С₁ = 2pс²h = 3,74·10^–10 Вт/м; С₂ = hc/k = 0,01438 м/К.

У цьому разі закон Планка можна подати у наступному вигляді:

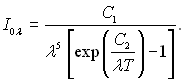(28.8)

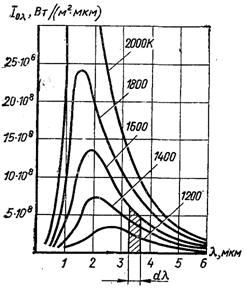
Рис.28.4. І_0l = f(l, T) згідно із законом Планка

Наведені на графіку (рис.28.4) ізотерми показують, що інтенсивність випромінювання дуже коротких хвиль швидко збільшується до максимуму, а далі повільно зменшується, не досягаючи нуля при найбільших довжинах хвиль, які ще відповідають тепловому випромінюванню.

Площа, обмежена віссю абсцис, ізотермою і ординатами l і dl (на рисунку заштрихована), служить мірою елементарної кількості енергії dE_0l,T, яка випромінюється одиницею поверхні в одиницю часу при температурі Т в інтервалі довжин хвиль dl, тобто dE_0l,T = І_0ldl. Енергія випромінювання E_0l,T у точці l може мати кінцеве значення тільки для певного фіксованого інтервалу довжин хвиль Dl, оскільки сумарна енергія випромінювання, яка має кінцеве значення, розподіляється за всім спектром. Отже, монохроматичне випромінювання для єдиної довжини хвилі є теоретично неможливим, тому що воно не має кінцевої енергії.

Під час аналізу математичного виразу закону Планка (28.8) звертають на себе увагу два випадки lТ >> C₂ і lТ << C₂. Коли lТ >> C₂, співвідношення C₂/(lТ) << 1. Якщо тепер величину exp[C₂/(lТ)] розкласти в степеневий ряд по C₂/(lТ):

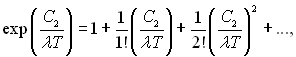
то у зв'язку з тим, що величина C₂/(lТ) дуже мала, можна обмежитися двома першими членами ряду. У цьому випадку залежність (28.8) переходить у формулу закону Релея-Джінса

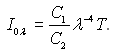(28.9)

Коли lТ > 100C₂, розходження з результатом розрахунку за точною формулою Планка не перевищує 10%.

У другому випадку, при lТ << C₂ значення exp[C₂/(lТ)] велике і одиницею в знаменнику виразу (28.8) можна знехтувати. У цьому разі отримаємо формулу Віна:

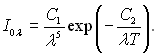(28.10)

Якщо lТ << 0,218C₂, то результат буде відрізнятися від розрахунку за формулою Планка менше, ніж на 1%.

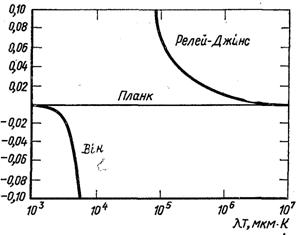
Рис.28.5. Області застосування законів Віна і Релея-Джінса

Області існування законів Віна і Релея-Джінса наведені на рис.28.5.

28.2.2. Закон зміщення Віна

Для кожної ізотерми (див. рис.28.4) при певній довжині хвилі настає максимальне значення інтенсивності випромінювання. При цьому екстремальне значення для більш високих температур зміщується в бік коротких хвиль. Щоб визначити найбільше значення інтенсивності випромінювання, необхідно прирівняти до нуля похідну dI_0l/dl.

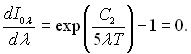
У цьому рівнянні довжина хвилі відповідає максимальній інтенсивності випромінювання, тобто l = l_макс, тоді рішення рівняння набуває виду:

С₂/(l_максТ) = 4,965

чи, підставивши значення С₂, матимемо

l_максТ = 2,8978·10^–3 м·К. (28.11)

Формула (28.11) – це математичний вираз, що відображає закон зміщення Віна. Закон установлює зв’язок між температурою випромінювання та довжиною хвилі, і відповідає найбільшій інтенсивності випромінювання.

Знаючи величину l_максТ, із закону Планка можна визначити значення максимальної інтенсивності випромінювання, якщо l_макс = 0,0028978/Т, то

тобто величина найбільшої інтенсивності випромінювання пропорційна п’ятій степені абсолютної температури чорного випромінювання.

28.2.3. Закон Стефана – Больцмана

Закон Планка установлює залежність інтенсивності випромінювання від довжини хвилі. Сумарна кількість енергії, випромінювана одиницею поверхні абсолютно чорного тіла в одиницю часу, визначається із закону Стефана – Больцмана. Цей закон був установлений Стефаном дослідним шляхом у 1879 р., а Больцманом – теоретично в 1884 р.

Повну кількість енергії, яка випромінюється абсолютно чорним тілом при температурі Т, можна знайти інтегруючи рівняння (28.8):

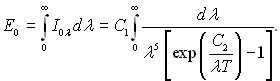
Введемо нову змінну א так, що тоді звідки 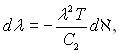але отже

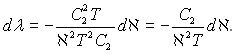
Підставимо отримані результати у вихідне рівняння:

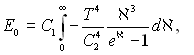
чи

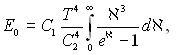
Розкладаючи підінтегральний вираз в ряд

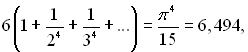
отримаємо

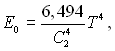
чи

, (28.12)

деs₀ – стала Стефана – Больцмана, рівна 5,668·10^–8 Вт/(м²·К⁴).

Повну кількість енергії, яка випромінюється абсолютно чорним тілом, прямо пропорціональна четвертій степені температури випромінювача.

У технічних розрахунках закон Стефана – Больцмана зручніше застосовувати в іншій формі:

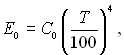(28.13)

де С₀ = s₀·10⁸ – коефіцієнт випромінювання абсолютно чорного тіла.

Закон Стефана – Больцмана можна використовувати для сірих тіл. Для цього вводиться поняття ступінь чорноти, яке визначається як відношення величини променевого потоку сірого тіла до значення променевого потоку абсолютно чорного тіла при тій же температурі, тобто

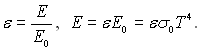
Отже

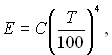(28.14)

де e – ступінь чорноти, e = 0...1; С коефіцієнт випромінювання сірого тіла, С = 0...5,668.

Методи термодинамічних досліджень використовуються для аналізу різних систем: класичних і квантових. Закони термодинаміки можна використовувати для випромінювання не тільки речовини, а і поля такого як електромагнітного, тобто теплового випромінювання.

Детальний аналіз випромінювання можливий на підставі квантової механіки, електродинаміки, статистичної фізики. Але, використовуючи поняття рівноваги, основне рівняння термодинаміки, метод термодинамічних потенціалів, можна пояснити деякі закони випромінювання.

Якщо в певній області випромінюючий простір знаходиться у рівновазі з оточуючими тілами, таке випромінювання називається рівноважним. При тепловій рівновазі двох тіл їх температури однакові. З точки зору термодинаміки рівноважне випромінювання представляє собою термодинамічну систему, яка характеризується деформаційною координатою – об’єм ом, термічною координатою – ентальпією, термічним потенціалом – температурою Т і узагальнюючою силою – тиском р (мається на увазі світловий тиск).

При такому підході до задачі напрошується зовнішня аналогія між рівноважним випромінюванням і газом. Маючи на увазі, що уявлення про квантову сторону випромінювання пов’язані з поняттям світлових частинок – фотонів, випромінювання в порожнині називають “фотонним газом”.

Закони електродинаміки дозволяють знайти рівняння стану для рівноважного випромінювання:

де U – внутрішня енергія системи.

Позначимо U/V через u, отримаємо

р = и/3,

де и – питома енергія рівноважного випромінювання.

Найбільше значення у технічних розрахунках має закон Стефана – Больцмана. Виведемо цей закон. Використаємо основне рівняння термодинаміки dU = TdS – pdV, в якому S – ентропія системи. Рівноважний процес випромінювання – ізотермічний, тоді

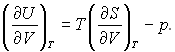(28.15)

З цього виразу неможна визначити, як змінюється ентропія. Необхідно замінити похідну в правій частині рівняння. Для цього необхідно мати термодинамічну функцію, в якій об’єм знаходиться під знаком диференціала, а ентропія – ні. Такою функцією є вільна енергія:

dF = –SdT – pdV.

Співвідношення взаємозамінності для цієї функції

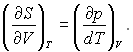
У цьому разі вираз (28.15) можна записати так:

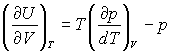
чи

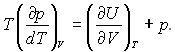
Але U = uV, тоді

Маючи на увазі, що и залежить тільки від температури, а р = и/3, отримаємо:

чи

Розділяючи змінні, після інтегрування отримуємо аналітичний вираз закону Стефана – Больцмана:

и = s₀Т⁴,

де s₀ – константа інтегрування, яка термодинамічним шляхом не визначається.