1.1 Кінематичний аналіз плоских споруд
При знаходженні напружено-деформованого стану (НДС) споруди її заміняють спрощеним поданням - розрахунковою схемою, вільною від другорядних невизначальних факторів, просторовою чи плоскою. Якщо осі всіх елементів споруди і навантаження розташовані в одній площині - це плоска розрахункова схема. Плоскі розрахункові схеми є найбільш простими і дозволяють в більшості випадків отримати задовільну для практики точність розрахунку.
Споруди (в подальшому - розрахункові схеми) в змозі сприймати навантаження лише в випадку, коли вони зберігають надану при їх спорудженні структуру, тобто геометричну форму і положення. Системи, що змінюються, не в змозі урівноважити зовнішні сили і при їх дії приходять в рух, змінюючи свою форму. Такі системи в будівництві не використовуються як споруди. Споруда має бути нерухомою відносно основи, структурно чи геометрично незмінною, а зміна її форми має йти лише за рахунок деформацій елементів. В геометрично незмінних спорудах малим деформаціям елементів відповідають малі переміщення точок споруди. Таким чином кінематичний аналіз споруди (розрахункової схеми) має передувати розрахунку її напружено-деформованого стану.
Змінність внутрішньої структури і рухомості споруди характеризується ступенем вільності – числом незалежних геометричних параметрів, що визначають положення всіх елементів споруди.
Геометрична незмінність споруди визначається в такій послідовності.
- В споруді виділяють диски – незмінний елемент споруди, який має три ступені вільності – два поступальні по осях ОХ, ОУ та кут повертання. Диском може бути стержень чи масивне тіло. Для забезпечення незмінності структури і нерухомості споруди диски з’єднуються шарнірами і стержнями, які обмежують ступені вільності. До землі диски прикріпляються опорними стержнями (рис.1.1.1). Шарніри бувають простими і кратними. Простий шарнір з’єднує два диски. Якщо шарнір з’єднує більше двох дисків – це кратний шарнір, він еквівалентний n-1 простому шарніру, де n – число дисків, які з’єднує шарнір. Простий шарнір обмежує два лінійних зміщення (він рівноцінний установці двох зв’язків), залишаючи взаємний кут повертання дисків.
Крім шарнірних з’єднань диски пов’язуються:
- простою припайкою (вона усуває три ступені вільності, виключаючи 2 лінійних та кутове переміщення);
- муфтою (усуває два ступені вільності, залишаючи одне лінійне переміщення уздовж осі муфти);
- кінематичною в’яззю (усуває один ступінь вільності - лінійне переміщення уздовж осі в’язі).
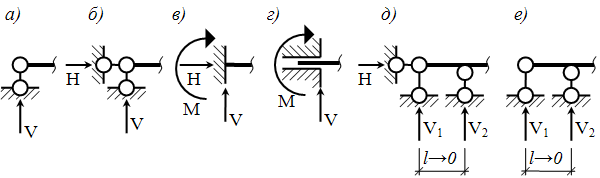
Рисунок 1.1.1 – Види опорних закріплень: а) - шарнірно рухома опора, б) - шарнірно нерухома опора, в) - жорстке нерухоме закріплення, г) - жорстке рухоме закріплення (проковзуюче закріплення), д, е) - шарнірно стержневі еквіваленти жорсткого та проковзуючого закріплень
Вищезгадані з’єднання можна взаємно замінювати, їх ще називають в’язями, а сили що в них виникають – реакціями (рис. 1.1.2). Так шарнірний зв’язок, що усуває 2 лінійні поступальні переміщення можна взаємо замінити двома кінематичними в’язями або навпаки. Кожний опорний стержень еквівалентний одному зв’язку, оскільки не допускає переміщення диска в напрямку стержня (рис.1.1.1 а-е).
Таким чином, ступінь вільності W споруди - кількісна оцінка кінематичного аналізу споруди, що складається із Д дисків, з’єднаних Ш простими шарнірами та має С0 опорних стержнів, можна визначити з формули П. Л. Чебишова [3, 8, 14]:
| W=3Д-2Ш-С0. | (1.1.1) |
Кількісну характеристику змінюваності системи – ступінь геометричної змінюваності Г можна визначити з модифікованої формули П. Л.Чебишова [3]:
| Г=3Д+2В-3П-2Ш-С-3, | (1.1.1, а) |
де Д – кількість простих дисків, включаючи опорний диск “землю”, якщо система прикріплена до неї; В – кількість матеріальних точок, тобто вузлів, в яких з’єднуються лише кінематичні в’язі; П – кількість простих припайок; Ш – кількість простих шарнірів; С – кількість кінематичних в’язів, (стержнів); 3 – число ступенів свободи всієї плоскої розрахункової схеми [3].
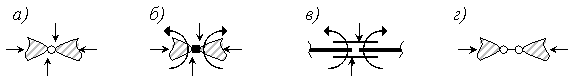
Рисунок 1.1.2 – Кінематичні в’язі: а) - шарнірна в’язь, б) - припайка, в) - муфта, г) - кінематична в’язь
Для ферм (стержневих систем, з’єднаних ідеальними шарнірами) ступінь вільності W:
| W = 2 Y – C - C0, | (1.1.2) |
де Y – число вузлів ферми,
С – число внутрішніх стержнів ферми,
С0 – число опорних стержнів.
Умова геометричної незмінності:
| W≤0. | (1.1.3) |
2. Виконання умови (1.1.3) необхідно, але недостатньо для забезпечення геометричної незмінності споруди, яка залежить не лише від числа зв’язків, накладених на диски, але й від їх розташування. Якщо умова (1.1.3) виконується, перевіряють ще геометричну структуру споруди (проводять якісну оцінку кінематичного аналізу). Для цього виділяють диски і досліджують їх з’єднання між собою, враховуючи основні принципи утворення структурно незмінних систем (рис. 1.1.3, а –в).
Два диски можна з’єднати жорстко шарніром С і стержнем АВ, вісь якого не проходить через центр шарніра (рис. 1.1.3, а).
Три диски можна з’єднати за допомогою трьох шарнірів, що не лежать на одній прямій (рис. 1.1.3, б).
Два диски можна жорстко з’єднати трьома стержнями, що не перетинаються в одній точці і не паралельні один одному (рис. 1.1.3, в). Це аналогічно рис. 1.1.3, а, оскільки два стержня можна замінити фіктивним шарніром в точці А.
Крім геометрично змінних та геометрично незмінних систем існують миттєво змінні системи. Такі системи одержимо, якщо три диски об’єднаємо трьома шарнірами, що лежать на одній прямій (рис. 1.1.3, г), або якщо два диски з’єднаємо трьома стержнями осі яких перетинаються в одній точці – миттєвому центрі обертання, (рис. 1.1.3, д). Миттєво змінні системи не є інженерними спорудами. Слід також пильнувати, щоб система не була близькою до миттєвої змінної. Тому кінематичний аналіз має включати аналіз і на миттєву змінність.
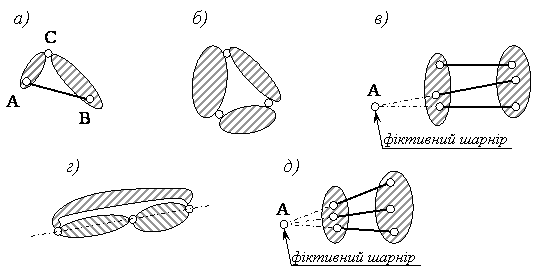
Рисунок 1.1.3 – Принципи утворення структурно-незмінних систем
Таким чином кінематичний аналіз включає етапи:
- визначення W- ступені вільності системи. Коли W > 0, аналіз завершено, так як система геометрично змінна;
- за умови W < 0 проводиться аналіз структури згідно принципів утворення незмінних систем. Коли система має незмінну структуру проводиться перевірка на миттєву змінність.
Статичною ознакою геометричної змінності є невизначеність зусиль або наявність нескінченно великих зусиль від кінцевого навантаження.
Для визначення реакцій у в’язях (basicreactions) використовуються рівняння статики (static’sequations).


