1.5 Розрахунок переміщень в статично визначених системах від постійних навантажень
1.5.2 Приклади розрахунку
1.5.2 Приклади розрахунку
– Накреслити розрахункову схему (stttlement scheme) споруди, вказати розміри та навантаження.
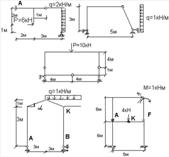
Рисунок 1.5.1 – Розрахункові схеми споруд.
– Необхідною умовою кінематичного аналізу системи є перевірка її за формулою П. Л. Чебишова:
| W= 3D-2Ш-С0, | (1.5.1) |
де W – ступінь вільності споруди;
D – кількість простих дисків;
Ш – кількість одиночних шарнірів (одиночний шарнір з’єднує два стержні);
С0 – кількість опорних стержнів системи.
Оскільки задані системи є несучими конструкціями, вони мають бути геометрично незмінними, тобто ступінь вільності споруди W має дорівнювати нулю.
W1=3·2-2·1-4=0; W2=3·2-2·1-4=0;
W3=3·3-2·3-3=0; W4=3·1-2·0-3=0; W5=3·4-2·4-4=0.
Достатньою умовою перевірки геометричної незмінності системи є перевірка її за способом утворення. Складні рами є комбінацією декількох простих рам. Складну раму можна розбити на прості лише одним способом. Для цього необхідно виділити основну раму (раму 1 поверху), до якої приєднується проста рама другого поверху і так далі.
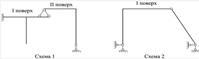
Рисунок 1.5.2 – Схеми взаємодії (поверхові схеми) для перших двох варіантів
Визначення опорних реакцій в складних рамах розпочинається з простих рам вищого поверху. Записуються рівняння рівноваги. Знайдені опорні реакції рам вищого поверху прикладаються у вигляді відпору до рам нижнього поверху і при розрахунку рам нижнього поверху розглядаються у вигляді зовнішнього навантаження, рис. 1.5.3.
Для побудови епюр M, Q, N позначають характерні перерізи рам.
Епюри моментів будуються зі сторони розтягнутого волокна. Згинальний момент в перерізі рами визначається як алгебраїчна сума моментів всіх сил, розташованих з однієї сторони перерізу.
Опорні реакції в рамах, які мають замкнений контур, визначаються загальним способом запису рівнянь статики:
∑M=0; ∑Y=0; ∑X=0. (1.5.2)
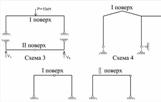
Рисунок 1.5.3 – Дослідження ступеня геометричної незмінності систем
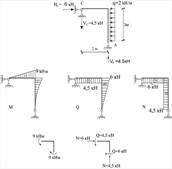
Рисунок 1.5.4 – Складова рама схеми 1
Розрахунок починається з рами другого поверху, рис. 1.5.4.
∑Mc
2VB – 3q*1,5=0; VB=4,5 кН.
∑Y=0;
HC – 2*3=0; HC=6 кН
∑X=0; – 2VC+3HC – 2*3*1,5=0; VC=4,5 кН
Далі розраховуються консолі рами першого поверху схеми 1.
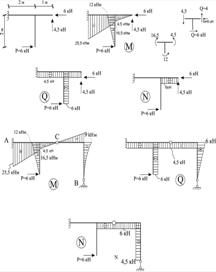
Рисунок 1.5.5 – Побудова епюр M, Q, N в рамі схеми 1
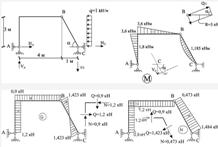
Рисунок 1.5.6 – Побудова епюр M, Q, N в простій арочній рамі з нахиленим стержнем (схема 2)
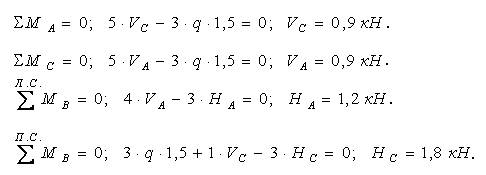
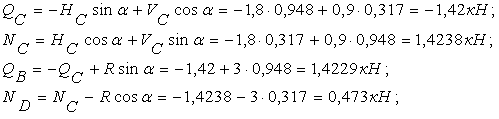
Для побудови епюр в складній рамі, що має вигляд замкненого контуру, її зручно розкласти на прості рами. В даному випадку немає можливості провести поверхове розділення складної рами, та для зручності розрахунку першою розраховується арочна рама АКВ. Опорні реакції HC, VC, HD, HD, які визначаються із розрахунку цієї арочної рами, прикладаються в зворотному напрямку до верхньої рами. Тоді опорні реакції в верхній рамі будуть уже відомі, можна проводити розрахунок.
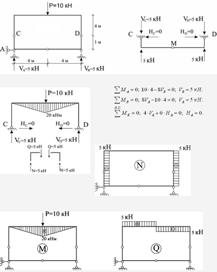
Рисунок 1.5.7 – Побудова епюр M, Q, N в складовій рамі, яка має замкнений контур
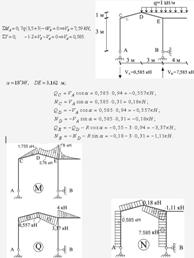
Рисунок 1.5.8 – Побудова епюр M, Q, N в простій балочній рамі з нахиленим елементом (схема 4)

Рисунок 1.5.9 – Побудова епюр M, Q, N в другому та першому поверхах складової рами схеми 5
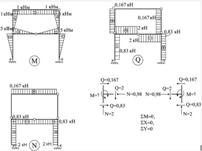
Рисунок 1.5.10 – Побудова епюр M, Q, N в складовій рамі схеми 5
Для визначення шуканого переміщення необхідно вибрати одиничний стан системи. Навантаження одиничного стану має прийматись таким, щоб воно здійснювало роботу на шуканому переміщенні.
Щоб визначити лінійні зміщення точок системи, наприклад, вертикальне зміщення точки Е в схемі 1, в шуканому напрямку прикладається одинична зосереджена сила Р=1 (рис. 1.5.11).
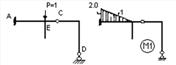
Рисунок 1.5.11 – Епюра М1 від одиничного навантаження рами силою Р=1 в точці Е в схемі 1
Для знаходження спільного кута повертання (tilt angles) перетинів А і С в схемі 2 прикладаються два одиничних зосереджених моменти в шуканих точках (рис. 1.5.12).
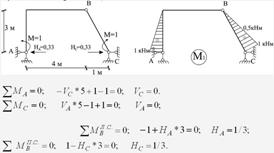
Рисунок 1.5.12 – Епюра М1 від одиничного навантаження точок А і С одиничними моментами в схемі 2
Для визначення кута перелому перетинів в шарнірі (наприклад, в шарнірі С в схемі 3) прикладається пара одиничних зосереджених моментів (рис. 1.5.13).
Для знаходження кутового переміщення системи, наприклад, кута повертання точки К в схемі 4, до шуканої точки прикладається одиничний зосереджений момент М=1 (рис. 1.5.14).
Щоб знайти зближення точок системи, яке знаходиться під дією зовнішніх навантажень, наприклад, зближення точок А і В в схемі 5, достатньо в шуканому напрямку прикласти дві одиничні зосереджені сили (рис. 1.5.15).
Шукане переміщення визначається за формулою Мора:
| (1.5.3) |
де ![]() – внутрішні зусилля в одиничному стані;
– внутрішні зусилля в одиничному стані;
Mp, Qp, Np – зусилля від зовнішнього навантаження в дійсному (вантажному) стані;
EI – згинальна жорсткість;
EA – жорсткість при розтягу чи стисненні;
GA – жорсткість при зсуві;
ρ – коефіцієнт форми перерізу.
При визначенні переміщень в рамах, балках з достатньою для інженерних розрахунків точністю в формулі Мора можна залишити лише першу складову:
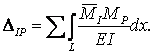 |
(1.5.4) |
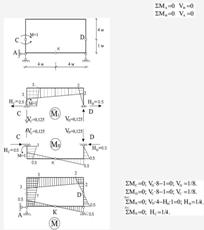
Рисунок 1.5.13 – Епюра М1 від одиничного навантаження шарніра С одиничними зосередженими моментами М=1 в схемі 3

Рисунок 1.5.14 – Епюра М1 від одиничного навантаження точки К одиничним зосередженим моментом М=1 у схемі 4
При цьому потрібно мати 2 стани системи: дійсний стан та одиничний
стан.
Техніка обчислення інтегралів за формулою Мора полягає в такому:
І. Перемноження дійсної і одиничної епюр можна проводити за правилом А. Н. Верещагіна:
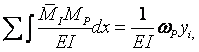 |
(1.5.5) |
де ωp– площа вантажної епюри ;
уі – ордината на епюрі ![]() під центром ваги площі вантажної епюри.
під центром ваги площі вантажної епюри.
Обмеження при використанні (1.4.5) полягає в тому, що:
- жорсткість стержня по його довжині має бути постійною;
- одна із епюр має бути прямолінійною, тоді друга може бути криволінійною, при цьому площу потрібно брати з криволінійної епюри.
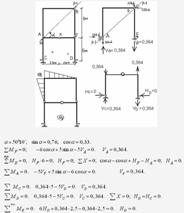
Рисунок 1.5.15 – Епюра М1 від одиничного навантаження точок А і В одиничними силами Р=1 за напрямком їх зближення у схемі 5
ІІ. Перемножити епюри можна користуючись формулою Карноухова– Сімпсона:
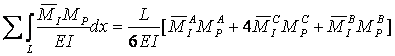 , , |
(1.4.6) |
де ![]() – ординати епюр моментів одиничного стану на початку, посередині, в кінці стержня;
– ординати епюр моментів одиничного стану на початку, посередині, в кінці стержня;
![]() – ординати епюр моментів вантажного стану на початку, посередині та в кінці стержня;
– ординати епюр моментів вантажного стану на початку, посередині та в кінці стержня;
l – довжина стержня.
Значення обчислених переміщень для схем.
Схема 1
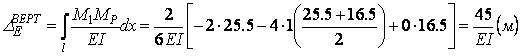
Схема 2.
![]()
![]() .
.
Схема 3.
![]()
![]() .
.
Схема 4.
![]()
![]() .
.
Схема 5.
![]() .
.


