2.1 Розрахунок статично невизначеної рами за методом сил
2.1.1 Склад завдання та приклад розрахунку
2.1.1 Склад завдання та приклад розрахунку
Рама – система зі стержнів, які жорстко або шарнірно з’єднані у вузлах.
Одним із перших методів розрахунку статично невизначених систем є метод сил. За основні (зайві) невідомі в методі сил (method of forces) беруть узагальнені реактивні сили в відкинутих зв’язках системи.
Число зайвих невідомих зв’язків називають ступенем статичної невизначеності. Для обчислення ступеня статичної невизначеності рам можна використовувати простішу формулу, ніж формула Чебишова [3]:
| nс = 3К - Ш, |
(2.1.1) |
де Л – число зайвих зв’язків.
К – кількість ізольованих контурів рами, для плоских стержневих систем – це кількість площин, обмежених стержнями рами або стержнями рами і “землею” (“землю” слід вважати одним простим диском) [3].
Ш – загальна кількість простих шарнірів (разом з опорними та шарнірами кінематичних в’язей. Одиночний простий шарнір з’єднує два диски). Шарнірно нерухому опору слід розглядати як простий шарнір, а шарнірно рухому – як два простих шарніри [3].
Розрахунок внутрішніх зусиль за методом сил в статично невизначеній рамі, зображеній на рис. 2.1.1, проводиться в такій послідовності:
а) ступінь статичної невизначеності (degree of static indefinability) рами:
| (2.1.2) |
б) для вибору основної системи методу сил відкинемо 6 зайвих зв’язків та розкладемо невідомі реакції в них на симетричні та кососиметричні пари, рис. 2.1.2. Це дасть можливість взяти до розгляду шість пар невідомих X1, X2, X3 , X4, X5,![]()
![]()
![]()
в) запишемо канонічні рівняння методу сил, які вказують на те, що переміщення за напрямком відкинутих зв’язків мають бути нульовими, оскільки в заданій рамі в цих точках знаходяться опори, які не допускають переміщень по вертикалі. В результаті отримуємо систему лінійних алгебраїчних рівнянь (equation) шостого порядку (2.1.3).
 |
(2.1.3) |
де ![]() – одиничні переміщення в основній системі методу сил в напрямку “і” від дії одиничної сили Xj = 1;
– одиничні переміщення в основній системі методу сил в напрямку “і” від дії одиничної сили Xj = 1;
![]() – вантажні переміщення в напрямку “і” від дії зовнішнього навантаження P, визначаються інтегруванням відповідних епюр за залежностями Максвела-Мора або за формулами числового інтегрування (за формулами Верещагіна, Мюллера-Бреслау чи Сімпсона-Карнаухова);
– вантажні переміщення в напрямку “і” від дії зовнішнього навантаження P, визначаються інтегруванням відповідних епюр за залежностями Максвела-Мора або за формулами числового інтегрування (за формулами Верещагіна, Мюллера-Бреслау чи Сімпсона-Карнаухова);
г) для визначення коефіцієнтів канонічних рівнянь (quotients of the initial equations) методу силбудуються епюри згинальних моментів в основній системі від парних одиничних зайвих невідомих Хi =1, i=1![]() 6 та від зовнішнього навантаження (external loading), рис. 2.1.3;
6 та від зовнішнього навантаження (external loading), рис. 2.1.3;
д) розв’язавши систему канонічних рівнянь методу сил одержимо корені системи:
е) кінцеві епюри згинальних моментів та поперечних сил будуємо за формулами:
| (2.1.4) |
| (2.1.5) |
де ![]() – епюра поперечних сил в окремому стержні від зовнішнього навантаження побудована в припущенні, що цей стержень шарнірно обпертий (articulated about);
– епюра поперечних сил в окремому стержні від зовнішнього навантаження побудована в припущенні, що цей стержень шарнірно обпертий (articulated about);
Мпр, Мл – кінцеві значення згинальних моментів в окремо взятому стержні справа і зліва;
ж) для побудови епюри поздовжніх сил доцільно розглядати рівняння рівноваги для кожного вузла (рис. 2.1.6) в кінцевій епюрі.
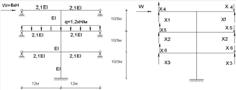
Рисунок 2.1.1 – Розрахункова схема Рисунок 2.1.2 – Основна система методу сил
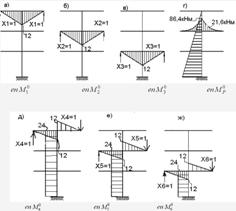
Рисунок 2.1.3 – Епюри згинальних моментів в основній системі методу сил від: а, б, в, д, е, ж – лінійних одиничних невідомих 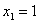 ,
, 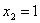 ,
, 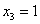 ,
, 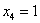 ,
, 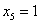 ,
, 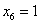 та г) – від зовнішнього навантаження
та г) – від зовнішнього навантаження

Рисунок 2.1.4 – Кінцева епюра згинальних моментів 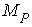 , статична перевірка вузлів та сумарна одинична епюра
, статична перевірка вузлів та сумарна одинична епюра 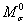
Кінематична перевірка епюри моментів: ![]()

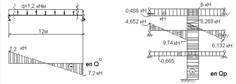
Рисунок 2.1.5 – Етапи отримання епюри поперечних сил Qр
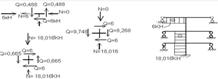
Рисунок 2.1.6 – Етапи побудови епюри поздовжніх сил Np


