1.6 Варіаційна задача будівельної механіки. Дослідження екстремуму функціонала (виразу потенціальної енергії балки) за методом Рітца
1.6.4 Метод Рітца
1.6.4 Метод Рітца
Метод Рітца - один з чисельних методів розв’язування диференціального рівняння Ейлера. За його допомогою варіаційна задача зводиться до задачі пошуку екстремуму функції. Основна ідея полягає ось у чому. Нехай y1, y2 - повна система функцій в зоні визначення функціоналу I(y), тобто кожна функція “у” з цієї зони може бути наближена з будь-яким ступенем точності лінійною комбінацією деяких функцій ui, які називають координатними:
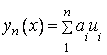 |
(1.6.9) |
Число п залежить від потрібної точності. Якщо цю лінійну комбінацію підставити у функціонал I(y), то він буде функцією лише параметрів ai :
| (1.6.10) |
Необхідною умовою того, що ця функція набуває екстремального значення відносно параметрів a1,a2,...,an, є виконання систем співвідношень
| f'(a1)=0; f'(a2)=0; f'(an)=0; | (1.6.11) |
З цієї системи нелінійних рівнянь визначаються параметри ai, їх ще називають ступенями вільності. Як правило, за фізичним змістом вони є вузловими лінійними та кутовими переміщеннями.
Ступінь вільності системи - це число незалежних геометричних параметрів, які повністю визначають можливі переміщення всіх її точок. Реальна пружна система завжди має нескінченне число ступенів вільності. Щоб чисельно розв’язати реальну задачу, деформований стан слід охарактеризувати переміщеннями скінченного числа точок, тобто число ступенів вільності вважається скінченним.
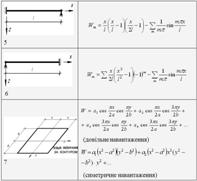
Координатні функції ui добираються так, щоб функція 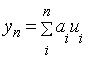 задовольняла граничні умови задачі. Так, координатні функції описують розподіл переміщень по зоні прогнутого стержня, коли одне з переміщень дорівнює одиниці, а інші дорівнюють нулю. Вирази для координатних функцій, застосовних в основних випадках розрахунків, вміщені в табл. 1.6.1.
задовольняла граничні умови задачі. Так, координатні функції описують розподіл переміщень по зоні прогнутого стержня, коли одне з переміщень дорівнює одиниці, а інші дорівнюють нулю. Вирази для координатних функцій, застосовних в основних випадках розрахунків, вміщені в табл. 1.6.1.
Приклад І. Знайти екстремум функціоналу
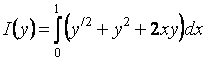 | y(0)=y(1)=0 |
Розв’язання. Припустимо, що використовуються координатні функції
Нехай n=2, тобто
Тоді
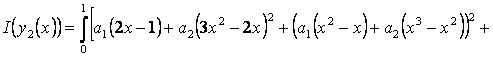
![]()
З умови ![]() і
і ![]() маємо:
маємо:
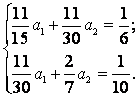
Таблиця 1.6.1 – Координатні функції
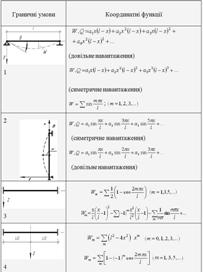
Продовження таблиці 1.6.1
Звідси: ![]() ;
; ![]() ;
;
![]() .
.
Отже, точний розв’язок:
Таблиця 1.6.2 – Результати порівняння точного та наближеного розв'язків
| i | y2(2i) | Точний розв'язок y2(2i) |
| 1 | -0.0285 | -0,0287 |
| 2 | -0,0506 | -0,0506 |
Приклад ІІ. Крайова задача прогину балки.
Знайти лінію прогину в балці, зображеній на рис. 1.6.3.
Граничні умови:
Розв’язати задачу у варіаційній постановці – означає знайти таку систему переміщень, яка мінімізує функціонал повної потенціальної енергії системи (potential energy of system).
Розв’язання.
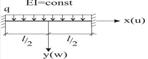
Рисунок 1.6.3 – Розрахункова схема навантаження балки
Цей функціонал для даної задачі
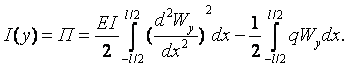 |
(1.6.12) |
Перший доданок в (1.6.12) є потенціальною енергією пружних деформацій, що дорівнює роботі внутрішніх сил, які діють на балку:
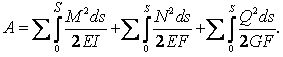 |
(1.6.13) |
У даному випадку другим і третім доданками в (1.6.13) можна знехтувати, оскільки за модулем вони досить малі. Другий доданок у (1.6.12) є потенціалом зовнішніх сил. Щоб розв’язати задачу, можна скористатися двома способами: 1) – мінімізувати функціонал; 2) – розв’язати диференціальне рівняння Ейлера-Лагранжа.
Наведемо приклад розв’язання першим способом. Доберемо координатну функцію у вигляді:
![]() ,
, ![]()
Нехай n=1, тоді ![]()
і переміщення ![]() .
.
Координатна функція задовольняє такі граничні умови:
![]() ;
; ![]() ;
;
![]() ;
;
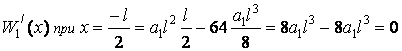 ;
; ![]()
![]() ;
;
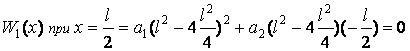 ;
;
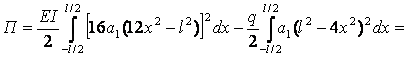
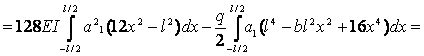
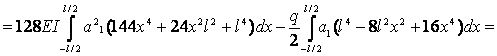
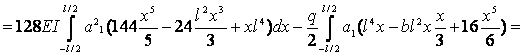
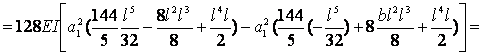
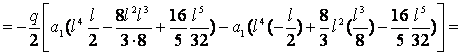
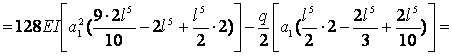
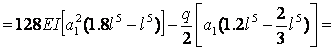
![]() ;
;
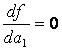 ;
; ![]() ;
;
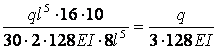 ;
; ![]() .
.
При x=0 (на середині балки) ![]() , що повністю відповідає точному розв'язку задачі згідно з класичним методом сил. Наведемо це розв’язання.
, що повністю відповідає точному розв'язку задачі згідно з класичним методом сил. Наведемо це розв’язання.
Балка, зображена на рис. 1.6.3, тричі статично невизначена.
Запишемо канонічні рівняння методу сил:
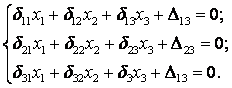
Щоб визначити коефіцієнти цих рівнянь, виберемо основну систему методу сил і побудуємо одиничні й вантажні епюри.
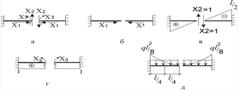
Рисунок 1.6.4 – Основна система методу сил (а) та епюри: 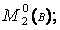
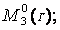
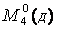
Визначаємо коефіцієнти канонічних рівнянь:
δ11=0·(M10=0); Δ1p; Δ2p; δ23=δ32=0; δ12=0; δ13=0;
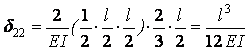 ;
;
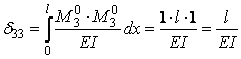 ;
;
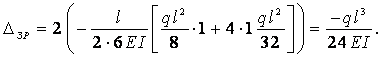
Отже, канонічна система запишеться у вигляді
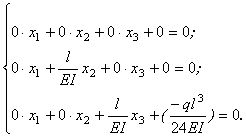
Корені системи: x1=0; x2=0; ![]() .
.
Далі маємо: ![]() ;
;
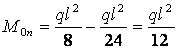 ;
; 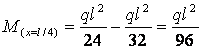 .
.
Шукані епюри зображено на рис. 1.6.5.
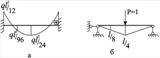
Рисунок 1.6.5 – Остаточні вантажна епюра Мр (а) та одинична епюра М1 в основній системі (б)
Щоб визначити переміщення середини балки, скористаємось формулою Сімпсона-Карнаухова
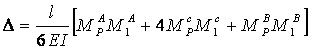 |
(1.6.14) |
де А, С, В – відповідно початок, середина та кінець стержня.
Побудуємо одиничну епюру в основній системі (див. рис. 1.6.5, б) і перемножимо за (1.6.14) з вантажною епюрою моментів Мр (див. рис. 1.6.5, а):
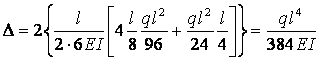 .
.Приклад ІІІ. Визначення стійкості системи з двома ступенями вільності.
Для системи з двома ступенями вільності, показаної на рис. 1.6.6, знайти критичні сили, при яких можливе відхилення від рівноважного стану системи. Опори С і D – пружно-піддатливі з коефіцієнтом твердості r (r – це реакція в опорі при одиничному переміщенні її по вертикалі).
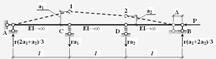
Рисунок 1.6.6 – Розрахункова схема системи з двома ступенями вільності
Розв'язання. Розв'яжемо задачу так званим методом варіацій функції
(варіацією називають нескінченно малу зміну функції при фіксованому значенні належної змінної х ).
Виконуємо дії за таким планом:
І. Обумовлюємо форму втрати стійкості з точністю до двох ступенів вільності а1 і а2 (їх фізична суть – це віртуальні лінійні переміщення точок С і D ). Тоді робота зовнішніх сил
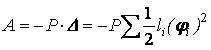 ,
,де φi - поворот системи при зміщенні її кінця.
Для першої ланки маємо ![]() , для другої
, для другої ![]() , для третьої
, для третьої ![]() .
.
Отже, 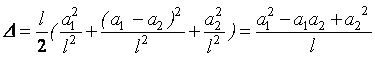 .
.
Робота внутрішніх сил: 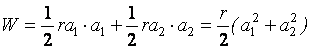 .
.
2. Записуємо вираз для потенційної енергії системи
у вигляді
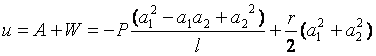 .
.3. З умов екстремуму функції u маємо: 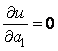 ;
; 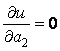 .
.
Тому отримуємо систему однорідних лінійних рівнянь відносно a1 і a2:
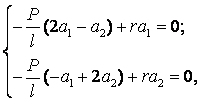
звідки
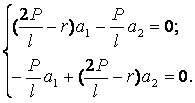
Щоб ця система мала відмінний від нуля розв’язок, необхідно, щоб її визначник дорівнював нулю, тобто:
 ,
,Або 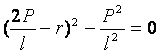 . Отже,
. Отже, ![]() ;
; ![]() .
.


