1.6 Варіаційна задача будівельної механіки. Дослідження екстремуму функціонала (виразу потенціальної енергії балки) за методом Рітца
1.6.3 Суть варіаційних методів розв'язування диференціальних рівнянь. Форма апроксимувальної функції
1.6.3 Суть варіаційних методів розв'язування диференціальних рівнянь. Форма апроксимувальної функції
Суть варіаційних методів розв'язування диференціальних рівнянь полягає в тому, що функція, яка задовольняє диференціальне рівняння при заданих граничних умовах, замінюється наближеним аналітичним виразом. Цей вираз добирається так, щоб він найкраще апроксимував дану функцію, тобто, щоб відхилення від істинного значення функції було найменшим.
При розв'язуванні цієї задачі зазвичай виникають два питання:
а) про вибір форми апроксимувальної функції;
б) про спосіб наближення цієї функції.
Кожне з цих питань потрібно досліджувати окремо, оскільки від форми апроксимувальної функції та від способу наближення залежить швидкість процесу збіжності результатів.
Практичне застосування варіаційних методів показує, що найзручнішою формою вираження апроксимувальної функції для будь-якого числа незалежних змінних є подання функції у вигляді ряду:
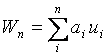 (i=1,2,3,...,n) (i=1,2,3,...,n) |
(1.6.6) |
де аі – невизначені сталі параметри, які варіюються згідно з прийнятим способом наближення;
ui– відповідні функції, які в сукупності найкраще зображують досліджувану функцію.
Розглянемо перше питання. Припустимо для визначеності, що йдеться про функцію від однієї незалежної змінної в проміжку [a,b], для якої відоме диференціальне рівняння
| F(x, W, W I,..., W IV)=0, | (1.6.7) |
та граничні умови W(a)=Wa; W(b)=Wb; ![]() ;
; ![]() ,
,
або інакше W(a) – Wa=0; W /(a) – W /a=0; W(b) – Wb=0; W /(b) – W /b=0;
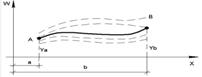
Рисунок 1.6.2 – Точний і наближений розв'язок диференціального рівняння (1.6.7)
Нехай W=f(x) - точний розв’язок цього рівняння (рис. 1.6.2, суцільна лінія АВ), а 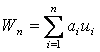 - довільний з наближених розв’язків (пунктир на рис. 1.6.2). Яку з ліній слід взяти за наближений розв’язок?
- довільний з наближених розв’язків (пунктир на рис. 1.6.2). Яку з ліній слід взяти за наближений розв’язок?
1-й спосіб. Вибираємо функції ui так, щоб кожна з них окремо задовольняла частину граничних умов. Диференціальне рівняння при цьому не задовольняється. Параметри аівизначаємо з умови, коли весь ряд в цілому найкраще апроксимує функцію як всередині, так і на кінцях проміжку.
2-й спосіб. Вибираємо функції ui так, щоб кожна з них окремо задовольняла всі граничні умови. Диференціальне рівняння при цьому не задовольняється. Параметри ai знаходимо з умови, коли весь ряд в цілому найкраще апроксимує функцію всередині проміжку.
3-й спосіб. Вибираємо функції uiтак, щоб кожна з них окремо задовольняла диференціальне рівняння, тобто була його частинним інтегралом. Граничні умови при цьому не задовольняються. Параметри ai знаходимо з умови, коли весь ряд в цілому найкраще апроксимує функцію на кінцях проміжку.
З вказаних способів побудови ряду перший найпростіший, оскільки він накладає на функцію найменше число обмежень. Проте умова для знаходження параметрів при цьому виходить менш простою.
Наведені міркування для випадку однієї змінної поширюються на випадок двох незалежних змінних. Відмінність лише в тому, що тут проміжок замінюється зоною площини, граничні точки - замкненим контуром цієї зони, а інтегральна лінія - інтегральною поверхнею.
Завжди весь ряд в цілому повинен якомога повніше відповідати очікуваному характеру зміни функції. Зауважимо, що при розв'язуванні практичних задач потрібні певні навички. Добре мати під руками довідкову таблицю, так званих, "підходящих" координатних функцій.
Так, наприклад, для вигину шарнірно обпертої балки координатну функцію можна записати у вигляді:
| (1.6.8) |
Для більшості практичних випадків рівняння Ейлера - Лагранжа неможливо розв’язати точно, тому доводиться використовувати чисельні методи. У таких випадках докладають зусиль, щоб уникнути розв’язування диференціальних рівнянь, а спробувати побудувати мінімізувальну послідовність.


