Розглянемо деякий визначений інтеграл

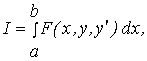(1.6.1)

з граничними умовами

Вираз типу (1.6.1) у варіаційному численні називають функціоналом (функція від функції).

Пошук умов, при яких функціонали набувають стаціонарного значення, і становить зміст задачі варіаційного числення. Вважається, що функція в точці має стаціонарне значення, якщо швидкість її зміни в цій точці дорівнює нулю (тобто дорівнюють нулю перші частинні по­хідні функції за всіма незалежними змінними).

Нехай маємо деяку функцію y(x), яка надає інтегралу (1.6.1) стаціонарного значення. Для того, щоб показати, що справді маємо ста­ціонарне значення, розглянемо деяку функцію y(x),відмінну відy(x), але водночас нескінченно близьку до неї (рис. 1.6.1).

,

(1.6.3)

де ε - довільна як завгодно мала величина, φ(x) деяка функція, що задовольняє умови неперервності й диференційованості. Різниця   називається варіацією функції y(x).  Лагранж ввів для неї позначення δy.

Дуже важливо, що величина δy має  так званий  віртуальний (можливий) характер, тобто, не пов’язана з жодними умовами і може бути довільною. Якщо функцію y(x) тлумачити як переміщення, то dyназиватиметься можливим переміщенням.

Більшість методів розв'язування варіаційних задач ґрунтується на використанні необхідних умов екстремуму, якими зазвичай бувають диференціальні рівняння (рівняння Ейлера) і граничні умови. Отже, варіаційна задача виявляється еквівалентною крайовій задачі для диференціального рівняння.

Диференціальне рівняння

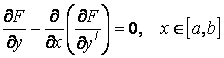(1.6.4)

виражає необхідну й достатню умову стаціонарності інтеграла при заданих граничних умовах. Тобто коли підінтегральна функція задовольняє рівняння (1.6.4), тоді функціонал (1.6.1) має стаціонарне значення.

Рівняння (1.6.4) отримали незалежно Л. Ейлер та Ж. Лагранж, тому воно називається рівнянням Ейлера-Лагранжа і відіграє фундаментальну роль у варіаційному численні.

Як приклад  можна навести варіаційну задачу Лагранжа про пошук мінімуму потенціальної енергії пружного стержня, еквівалентну дифе­ренціальному рівнянню рівноваги, записаному в переміщеннях з відпо­відними граничними умовами. Рівняння рівноваги вигнутого стержня (балки) має вигляд:

.

(1.6.5)

Знак "+" відповідає випадку, коли вісь у  спрямована вгору. Тоді знаки моменту М та другої похідної у" збігаються.

Функціоналом для рівняння (1.6.5) при розв'язуванні цієї задачі буде вираз повної потенціальної енергії пружної балки, розв’язок рів­няння (1.6.5) - знайдена пружна лінія балки y(x)- забезпечить мінімум потенціальної енергії балки. Іншими словами, рівняння рівноваги – це рівняння Ейлера-Лагранжа для відповідного функціоналу. До них потрібно ще приєднати граничні умови, які можна отримати з виразу енергії.

Отже, повна потенціальна енергія системи дає повну інформацію про систему, оскільки дозволяє отримати не тільки рівняння рівноваги, а й конкретні граничні умови задачі.