2.2 Розрахунок нерозрізної балки на постійне та тимчасове навантаження
2.2.2 Розрахунок нерозрізної балки на зовнішнє постійне навантаження
2.2.2 Розрахунок нерозрізної балки на зовнішнє постійне навантаження
Початкова стадія розрахунку нерозрізних балок (not cutting beam) на зовнішнє навантаження в матричній формі пов'язана з визначенням ступеня статичної невизначеності і вибором основної системи (basic system). Ця стадія розрахунку нічим не відрізняється від розрахунку нерозрізних балок звичайним способом.
Нехай для нерозрізної балки виконана перша стадія розрахунку. Для n разів статично невизначної нерозрізної балки при навантаженні її одним варіантом зовнішніх сил система канонічних рівнянь в матричній формі має вигляд:
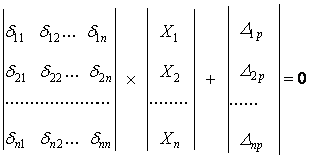
або ![]() (2.2.1)
(2.2.1)
де Аδ - матриця одиничних переміщень в основній системі від Х1 = Х2 = Х3 = Хn = 1; ![]() - вектор невідомих зусиль;
- вектор невідомих зусиль;
![]() - вектор переміщень в основній системі від зовнішнього навантаження за всіма напрямами Х1, Х2, … Хn.
- вектор переміщень в основній системі від зовнішнього навантаження за всіма напрямами Х1, Х2, … Хn.
Матрицю одиничних переміщень можна записати:
| (2.2.2) |
де Lm01- матриця, транспонована відносно Lm0;
В - матриця піддатливості окремих елементів (ділянок), на які розділяють задану систему, характеризує геометричні розміри і матеріал конструкції;
Lm0 - матриця впливу згинальних моментів в основній системі від кожної сили Х1 = Х2 = … = Хn=1 окремо.
Вектор ![]() можна подати у вигляді
можна подати у вигляді
| (2.2.3) |
Розв’язання матричного рівняння (2.2.1) дає вектор невідомих
| (2.2.4) |
Вектор згинальних моментів в пронумерованих перерізах нерозрізної балки
| (2.2.5) |
| (2.2.6) |
або
| (2.2.7) |
За вектором ![]() будується кінцева епюра згинальних моментів. Вираз (2.2.6) – алгоритм розрахунку статично невизначених систем методом сил в матричній формі. Для його реалізації на ЕОМ треба скласти чотири початкові матриці L0m, В, L0mp , Р.
будується кінцева епюра згинальних моментів. Вираз (2.2.6) – алгоритм розрахунку статично невизначених систем методом сил в матричній формі. Для його реалізації на ЕОМ треба скласти чотири початкові матриці L0m, В, L0mp , Р.
Після отримання значення ![]() проводиться деформаційна перевірка правильності отриманої епюри:
проводиться деформаційна перевірка правильності отриманої епюри:
| (2.2.8) |
При дії на статично невизначену систему кожного з t варіантів зовнішніх дій (до них відносяться постійні навантаження, тимчасові, осідання опор і температура) система канонічних рівнянь має вигляд:
| (2.2.9) |
де Х – матриця невідомих, має t стовпців;
![]() – матриця одиничних переміщень в основній системі від Х1, Х2, … Хn = 1;
– матриця одиничних переміщень в основній системі від Х1, Х2, … Хn = 1;
![]() –матриця переміщень від всіх t варіантів навантажень в основній системі;
–матриця переміщень від всіх t варіантів навантажень в основній системі;
![]() –матриця впливу згинальних моментів в основній системі від всіх t варіантів навантажень
–матриця впливу згинальних моментів в основній системі від всіх t варіантів навантажень ![]() , прикладених роздільно;
, прикладених роздільно;
Р – матриця всіх t варіантів зовнішніх дій.
Розв’язання системи (2.2.9) аналогічне розв’язанню (2.2.4):
| (2.2.10) |
де Х і Δ – матриці.
Згинальні моменти для всіх k перерізів від всіх t варіантів зовнішніх навантажень отримаємо у вигляді матриці:
 . . |
(2.2.11) |
Розглянемо приклад матричного розрахунку нерозрізної балки на постійне і тимчасове навантаження (рис. 2.2.1). Схему балки показано на рис. 2.2.1, а. Розділимо перший і другий прогони на 5 рівних частин, консоль – на 2 частини і пронумеруємо перерізи, в яких будемо визначати згинальні моменти. Основна система і характерні перерізи зображені на рис. 2.2.1, б.
Для визначення початкових матриць ![]() побудуємо епюри моментів в основній системі окремо від таких величин:
побудуємо епюри моментів в основній системі окремо від таких величин:
1) Х1=1 (рис. 2.2.1, в) - ![]() ;
;
2) Х2= 1 (рис. 2.2.1, г) - ![]() ;
;
3) постійного одиничного розподіленого навантаження (рис. 2.2.1, д) - Мq0 постійне;
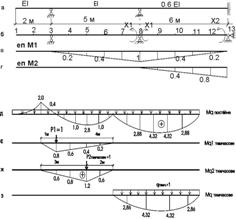
Рисунок 2.2.1 – Розрахункова схема і епюри моментів: а – схема нерозрізної балки; б – основна системи балки; в – еп. моментів М1; еп. моментів М2; д – епюра М від одиничного постійного навантаження (qпостійне = 1); е – епюра М від одиничної тимчасової зосередженої сили (Р1 =1); ж – епюра М від одиничної тимчасової зосередженої сили (Р2 =1); з – епюра М від одиничного тимчасового навантаження (qтимчасове = 1)
4)тимчасової одиничної зосередженої сили Р1 (рис. 2.2.1, е) – Мр10тимчасове;
5) тимчасової одиничної зосередженої сили Р2 (рис. 2.2.1, ж) – Мр20тимчасове;
6) тимчасового одиничного розподіленого навантаження qтимчасове (рис. 2.2.1.з) – Мq0тимчасове і обчислимо ординати цих епюр в характерних перерізах.
Для зручності побудови епюр моментів від розподіленого навантаження на рис. 2.2.2 показано проміжні точки квадратної параболи (по середині а=ql2/8). Матриця впливу згинальних моментів Lm0 складена за епюрами ![]() та
та ![]() від Х1 = Х2 = 1 (рис. 2.2.1, г):
від Х1 = Х2 = 1 (рис. 2.2.1, г):
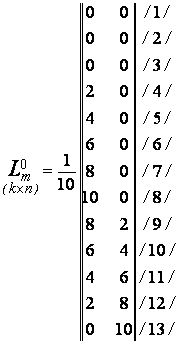 . . |
(2.2.12) |
де k,n – порядок прямокутної матриці Lm0.
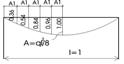
Рисунок 2.2.2 – Проміжні точки квадратної параболи
Матрицю піддатливості (pliability) В для всієї балки подамо у вигляді трьох матриць В1, ВІІ , ВІІІ для: консолі, 1 і 2 прогонів
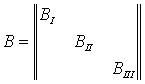 . . |
(2.2.13) |
Матриця ![]() складається з двох матриць другого порядку
складається з двох матриць другого порядку ![]() і
і ![]() , що відповідають двом ділянкам консолі:
, що відповідають двом ділянкам консолі:
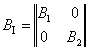 ; ; 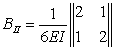 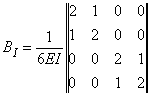 |
(2.2.14) |
Матриці ![]() складаються кожна з п’яти матриць другого порядку:
складаються кожна з п’яти матриць другого порядку:
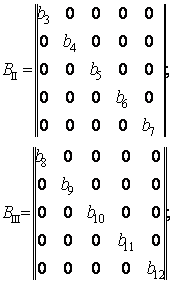 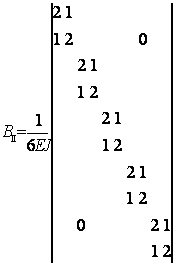 ; ;  |
(2.2.15) |
Зважаючи на велике число ділянок розділення (нерозрізна балка має 13 характерних перерізів) матриця піддатливості В виходить дуже громіздкою, що ускладнює процес розрахунку. Для полегшення розрахунків знизимо її порядок. Це можливо, оскільки одиничні і вантажні епюри неперервні на межі ділянок bi і bi+1.
Складемо кутові елементи суміжних матриць bi і bi+1 за схемою
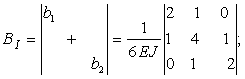
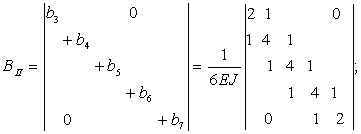
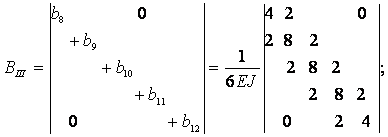
Аналогічно складемо кутові елементи суміжних матриць Bi іBi+1 в сумарній матриці жорсткості:
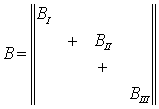 ;
;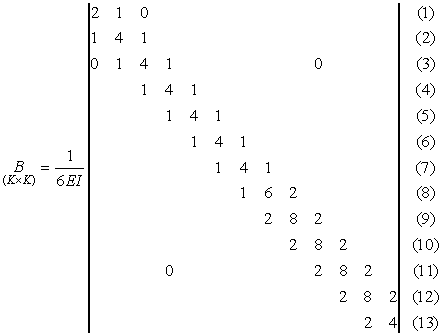 |
(2.2.16) |
Матрицю одиничних переміщень визначимо за (2.2.2):

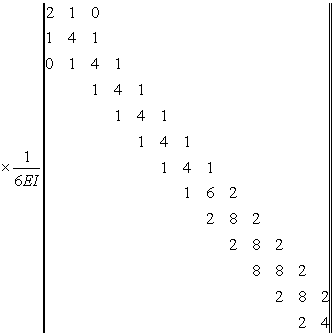 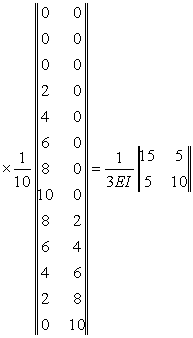 ; ; |
(2.2.17) |
Для обчислення добутку матриць зручно скористатися ЕОМ. Якщо розміри матриць, що перемножуються, невеликі, то
і можна скористатися оберненою матрицею одиничних переміщень ![]() . Матриця, обернена до одиничної:
. Матриця, обернена до одиничної:
<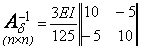 ./td> ./td>
| (2.2.18) |
При складанні матриці впливу згинальних моментів від одиничних значень навантажень А0mpзвернемо увагу на епюри ![]()
Матриця А0mp буде складатися з 4 стовпців – за числом епюр моментів від заданих навантажень: ![]() і 13 рядків – за числом вибраних характерних перерізів./
і 13 рядків – за числом вибраних характерних перерізів./
В даному прикладі перший стовпець матриці А0mp відповідає епюрі М в балці в 13 характерних перерізах від навантаження власної ваги ![]() другий стовпець – епюрі М від зосередженої сили Р1 і т.д.
другий стовпець – епюрі М від зосередженої сили Р1 і т.д.
 . . |
(2.2.19) |
Матриця Р від чотирьох варіантів заданих навантажень
 . . |
(2.2.20 |
Матрицю невідомих Х отримаємо за (2.2.10):
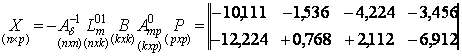 . . |
(2.2.21) |
Матриця шуканих згинальних моментів визначається за (2.2.15):
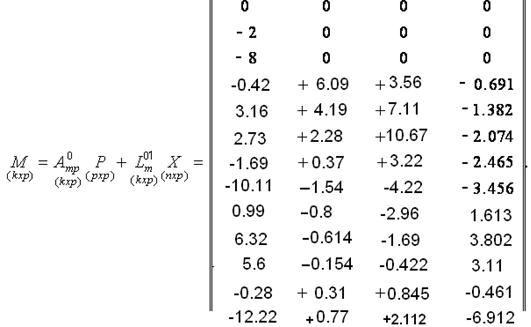 |
(2.2.22) |
Епюри від заданих навантажень наведені на рис. 2.2.3.
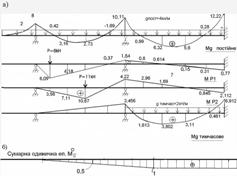
Рисунок 2.2.3 а – Епюри моментів від постійних та тимчасових навантажень;
б – сумарна одинична епюра моментів в основній системі методу сил від лишніх невідомих – зосереджених одиничних моментів на опорах
На рис.2.2.3, а подано сумарну одиничну еп. ![]() для можливості проведення деформаційної перевірки. Суть деформаційної перевірки – рівність нулю взаємних кутів повертання на опорах – добуток еп.
для можливості проведення деформаційної перевірки. Суть деформаційної перевірки – рівність нулю взаємних кутів повертання на опорах – добуток еп. ![]() на кінцеву епюру згинальних моментів за умови правильної її побудови має бути рівна нулю, відхилення допускається в межах 3%. Деформаційна перевірка еп.
на кінцеву епюру згинальних моментів за умови правильної її побудови має бути рівна нулю, відхилення допускається в межах 3%. Деформаційна перевірка еп. ![]() :
:


