2 РОЗРАХУНОК СТАТИЧНО НЕВИЗНАЧЕНИХ СИСТЕМ
2.2 Розрахунок нерозрізної балки на постійне та тимчасове навантаження

2.2.3 Розрахунок нерозрізної балки на тимчасове навантаження (time loading). Побудова ліній впливу

Задача про побудову ліній впливу /л.в./ зводиться до знаходження  функціональної залежності між шуканим зусиллям і вантажем, що переміщається по нерозрізній балці Р = 1.

Оскільки нерозрізна балка статично невизначена, спочатку визначають залежність між зусиллями в "зайвих" зв'язках (вектор Х ). За знайденим значенням Х  будують лінії впливу заданого зусилля.

Лінії впливу зусиль в "зайвих" зв'язках  для  n  разів статично невизначної системи визначають за виразом:

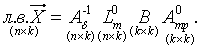  (2.2.23)  

Позначення матриць (2.2.23) наведені раніше. Вектор згинальних моментів в пронумерованих перерізах статично невизначеної системи визначається за виразом:

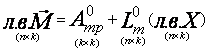  . (2.2.24)  

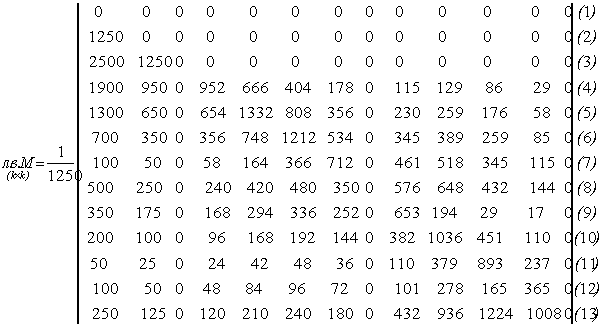
Для прикладу побудуємо лінії впливу опорних і прогонового моментів Мв  для нерозрізної балки, наведеної на рис. 2.2 1.  Матриці Аδ-1  і  В  наведені в (2.2.16) і (2.2.18). Для побудови  А0mp  завантажимо нерозрізну балку в характерних перерізах одиничною рухомою силою  Р=1 і  побудуємо епюри моментів (рис. 2.2.4). За отриманими епюрами будуємо матрицю  А0mp  порядку  :

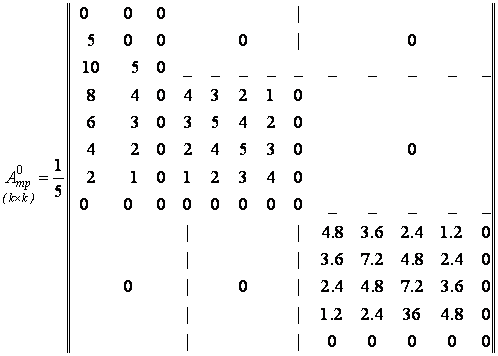  (2.2.25)  
      
Highslide J
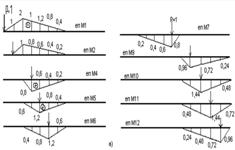
Рисунок 2.2.4, а – Епюри моментів від нерухомого навантаження

Highslide J
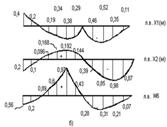
Рисунок 2.2.4, б - Лінії впливу Х1, Х2, М6

Підставимо обчислені значення      в  (2.2.23):

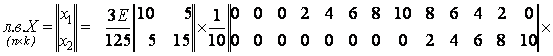
Згідно з (2.2.24) вектор

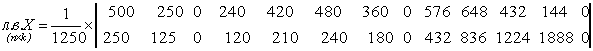
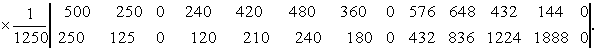
Лінії впливів опорних моментів, Х1, Х2 і прогонового Мв  показані на рис. 2.2.4, б. Побудову ліній впливу Х  та  М зручно виконувати за допомогою персонального комп’ютера.

Оскільки довільна завада на шляху деформацій призводить до виникнення внутрішніх зусиль, установлення додаткових опор в нерозрізній балці  порівняно зі статично визначеною розрізною балкою веде до появи в додаткових опорах реакцій та перерозподілу внутрішніх зусиль між елементами нерозрізної статично невизначеної балки.

Матрична форма розрахунку дає можливість розглядати напружено-деформований стан (strains – deformedstate) нерозрізної балки в вигляді сукупності окремих ділянок з постійною жорсткістю (постійними геометричними розмірами та модулем пружності).

Матрицю піддатливості В можна отримати з виразу потенціальної енергії системи та його мінімізації або за формулами будівельної механіки для визначення переміщень, оскільки коефіцієнти матриці піддатливості В () – це переміщення в напряму “і” від дії в напряму “j” одиничної узагальненої сили.