2.3 Розрахунок статично невизначеної рами за методом переміщень
2.3.2 Приклад розрахунку
2.3.2 Приклад розрахунку
1. Накреслити розрахункову схему рами (рис. 2.3.1), вказати задані розміри та навантаження.
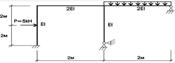
Рисунок 2.3.1 – Розрахункова схема рами
Для розрахунку рами методом переміщень необхідно визначити число невідомих кутових і лінійних переміщень (linearmoving). З цією метою підраховується число жорстких вузлів рами. Жорстким вважається вузол, в якому сходяться жорстко закріплені кінці стержнів. Число жорстких вузлів для наведеної рами nж = 2 (рис. 2.3.2).
У всі жорсткі вузли рами, включаючи опорні, вводять шарніри. Далі досліджується ступінь геометричної змінності такої модифікованої рами.
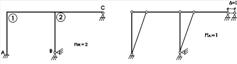
Рисунок 2.3.2 – Послідовність визначення кінематичної невизначеності при розрахунку методом переміщень: а - визначення числа жорстких вузлів; б - підрахунок числа лінійних переміщень рами
Задана рама після встановлення в неї шарнірів отримує можливість вільного переміщення по горизонталі, отже, ступінь її геометричної змінності (degreeofgeometricalconvertibility) nл = I.
Ступінь кінематичної невизначеності за методом переміщень
| n = nж + nл = 2+1 = 3. | (2.3.1) |
Для вибору основної системи методу переміщень в жорсткі вузли рами і за можливими напрямками лінійних зсувів вводимо додаткові зв'язки, що перешкоджатимуть кутовим і лінійним переміщенням.
Після накладання додаткових зв’язків рама перетворюється на сукупність стержнів, жорстко закріплених двома або одним кінцем. За невідомі, в основній системі методу переміщень, беремо невідомі кутові і лінійні переміщення, які виникли в додатково накладених зв'язках після прикладення навантаження.
До остаточного визначення вважаємо їх рівними одиниці.
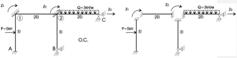
Рисунок 2.3.3 – Вибір основної системи: а - основна система методу переміщень; б - сукупність стержнів, жорстко затиснених двома або одним кінцем
Заздалегідь напрям повороту приймаємо за рухом годинникової стрілки, можливе лінійне переміщення приймаємо зміщення зліва направо.
Дійсні напрями кутових і лінійних переміщень уточнюються розрахунком.
2. Основну систему методу переміщень (рис. 2.3.3) завантажуємо по черзі кутовими і лінійними одиничними зміщеннями, а також зовнішнім навантаженням. За таблицями реактивних зусиль зігнутих стержнів будуються епюри моментів ![]() в основній системі від одиничних вимушених переміщень і силового навантаження (рис. 2.3.4 ).
в основній системі від одиничних вимушених переміщень і силового навантаження (рис. 2.3.4 ).
3. Система канонічних рівнянь методу переміщень, яка виражає умову рівності нулю реакцій в додаткових зв'язках, має такий вигляд:
 |
(2.3.2) |
де ![]() – реактивне зусилля в i–му додатковому зв'язку, викликане одиничним вимушеним переміщенням j–го зв'язку;
– реактивне зусилля в i–му додатковому зв'язку, викликане одиничним вимушеним переміщенням j–го зв'язку;
i=1, 2, 3…n; j=1, 2, 3…n. Zi – реактивне зусилля і–го зв'язку;
Rip – вантажний член, реактивне зусилля в i–му зв'язку, викликане навантаженням.
В матричній формі система канонічних рівнянь: ![]()
 |
(2.3.3) |
де R – матриця, складається з коефіцієнтів канонічних рівнянь;
![]() – вектор, включає вантажні складові;
– вектор, включає вантажні складові;
![]() – вектор шуканих переміщень.
– вектор шуканих переміщень.
Стосовно даного прикладу система канонічних рівнянь
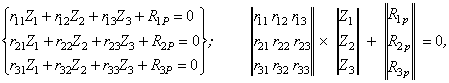
де r11 , r12, r13, R1р – реактивні моменти, які виникають в першому додатково накладеному зв'язку від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М1=0; r21 , r22, r23, R2р - реактивні моменти в додатково введеному жорсткому затисненні вузла 2 від одиничних зсувів і навантаження. Визначаються при розгляді рівноваги відповідного вузла (рис. 2.3.5) ∑М2=0; r31, r32, r33, R3р - реактивні сили, які виникають в третьому додатково введеному зв'язку - в опорному горизонтальному стержні. Визначаються при розгляді рівноваги всіх сил на вісь додатково введеного стержня (рис. 2.3.5) ∑Х = 0.
Реактивне зусилля в додатковому зв'язку вважається додатним, якщо напрям його дії збігається з вибраним напрямом повороту або лінійним зміщенням вузла.
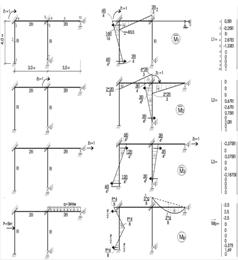
Рисунок 2.3.4 – Одиничні і вантажні епюри моментів в основній системі методу переміщень. Матриці впливу одиничних переміщень по характерних перетинах
4. Розв'язання системи канонічних рівнянь проводимо за допомогою комп’ютера
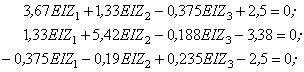
Перевірка правильності розв'язання системи здійснюється шляхом підстановки знайдених невідомих в систему рівнянь (дозволяється похибка 1-1,5%).
5. Епюра згинальних моментів (рис. 2.3.6) будується за формулою
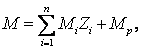 |
(2.3.4) |
де ![]() – епюри згинальних моментів в основній системі від одиничних значень i-х переміщень;
– епюри згинальних моментів в основній системі від одиничних значень i-х переміщень;
n – число одиничних переміщень, тобто ступінь кінематичної невизначеності рами;
zi – знайдені значення кутових і лінійних переміщень вузлів рами;
Мр – епюра згинальних моментів в основній системі від зовнішнього навантаження.

Рисунок 2.3, а – Визначення коефіцієнтів канонічних рівнянь методу переміщень

Рисунок 2.3. б – Визначення коефіцієнтів канонічних рівнянь методу переміщень
Для даної рами: М =МП1 Z1+MП2 Z2 +MП3 Z3+ МПр. (2.3.5)
Епюра моментів в матричній формі
| (2.3.6) |
де L0 – матриця, елементи якої є ординатами епюри моментів в характерних перерізах основної системи при Р = I;
![]() - вектор зовнішнього навантаження;
- вектор зовнішнього навантаження;
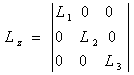 , , |
(2.3.7) |
- матриця впливу одиничних переміщень, складається з матриць впливу.
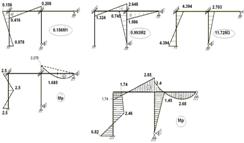
Рисунок 2.3.6 – Етапи побудови епюри моментів
6. Статична перевірка включає розгляд рівноваги вузлів рами (рис. 2.3.7).
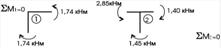
Рисунок 2.3.7 – Статична перевірка рівноваги вузлів
Правильність отриманої епюри моментів необхідно підтвердити також кінематичною перевіркою визначення будь-якого переміщення в дійсності явно рівного нулю. Для цього вибирається основна система методу сил і будується епюра моментів в одному з одиничних станів (рис. 2.3.8). Обчислення переміщення виконується за формулою Максвела – Мора. Розбіжність між додатною і від’ємною величинами не повинна перевищувати 3% від більшої з них.
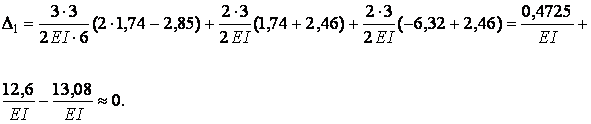
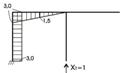
Рисунок 2.3.8. – Одинична епюра моментів в основній системі методу сил.
Помилка складає: ![]() від (+13,73) 1,82% , що менше 3%.
від (+13,73) 1,82% , що менше 3%.
7. Поперечні сили (рис. 2.3.9) визначаються за формулою:
| (2.3.8) |
де Qх - поперечна сила в будь-якому перерізі стержня;
Qx0- поперечна сила в простій балці;
Mпр, Mлів, - згинальні моменти на правому і лівому кінцях даного стержня;
l - довжина даного стержня.
Стояк лівий:
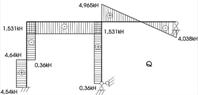
Рисунок 2.3.9 – Епюра поперечних сил в заданій рамі
Ригель лівий ![]()
Стояк правий ![]() .
.
Ригель правий
Поздовжні сили в стержнях обчислюються з розгляду рівноваги вузлів (рис. 2.3.10).
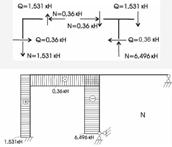
Рисунок 2.3.10 – Епюра поздовжніх сил в заданій рам


