2.4 Розрахунок несучої здатності статично невизначеної рами з урахуванням пластичної роботи матеріалу
2.4.2 Розрахунок несучої здатності рами прямим методом
2.4.2.1 Алгоритм розрахунку
2.4.2 Розрахунок несучої здатності рами прямим методом
2.4.2.1 Алгоритм розрахунку
Алгоритм розрахунку несучої здатності рами прямим методом коротко можна описати так [36]:
1. Виконується статичний розрахунок рами з параметром навантаження ΔF.
2. Для кожного з розрахункових перерізів рами записується умова пластичності
| (2.4.2) |
де ![]() – величина граничного моменту в перерізі "j";
– величина граничного моменту в перерізі "j";
![]() – момент, що виникає в перерізі "j" від дії навантаження з параметром ΔF;
– момент, що виникає в перерізі "j" від дії навантаження з параметром ΔF;
s – кількість розрахункових перерізів рами.
Встановлюється величина навантаження, ![]() що відповідає появі першого пластичного шарніру
що відповідає появі першого пластичного шарніру
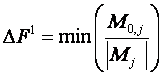 , (j=1, 2,. . ., s). , (j=1, 2,. . ., s). |
(2.4.3) |
Перший пластичний шарнір утворюється в перерізі, де виконується умова (2.4.3).
3. Будується епюра моментів ![]() , що відповідає навантаженню
, що відповідає навантаженню ![]() .
.
| (2.4.4) |
4. В перерізі, де утворився пластичний шарнір, встановлюється простий шарнір. Тим самим усувається можливість зміни згинального моменту в даному перерізі при подальшому зростанні параметра навантаження.
5. Якщо рама чи її частина стала геометрично змінною, потрібно перейти до п. 10.
6. Виконується статичний розрахунок рами із встановленим шарніром при дії параметру навантаження ![]() .
.
7. Встановлюється переріз, де утворюється наступний пластичний шарнір і приріст параметру навантаження ![]() , що призводить до його появи. Для цього використовується залежність
, що призводить до його появи. Для цього використовується залежність
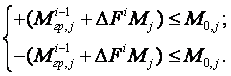 |
(2.4.5) |
З використанням (2.4.5) визначається найменше додатне значення ![]() і переріз, де утворюється пластичний шарнір.
і переріз, де утворюється пластичний шарнір.
8. Будується епюра моментів ![]() , що відповідає параметру навантаження
, що відповідає параметру навантаження 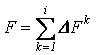
| (2.4.6) |
9. Розрахунок повторюється, починаючи з п. 4.
10. Параметр навантаження і епюра моментів, одержані в п. 8, є граничними для даної рами.


