2.4 Розрахунок несучої здатності статично невизначеної рами з урахуванням пластичної роботи матеріалу
2.4.2 Розрахунок несучої здатності рами прямим методом
2.4.2.4 Приклад розрахунку
2.4.2 Розрахунок несучої здатності рами прямим методом
2.4.2.4 Приклад розрахунку
Для рами (рис. 2.4.1) знайти граничне навантаження і побудувати пластичний механізм руйнування рами.

Рисунок 2.4.1 – Задана рама
1. Виражаємо діюче навантаження через параметр F: F1=5F, F2=F.
2. Ступінь статичної невизначеності рами n=5+2×0 - 3×1=2.
3. Число пластичних шарнірів k=2+1=3.
4. Співвідношення жорсткостей ригеля і стояків
5. Граничні згинальні моменти для стояків і ригеля
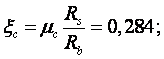
![]()
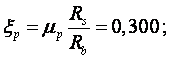
![]()
Б. 7. Будуємо основну систему методу сил (рис. 2.4.2).
Записуємо систему канонічних рівнянь методу сил
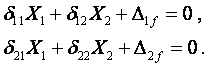
Будуємо одиничні та вантажну епюри моментів (рис. 2.4.3):
Рисунок 2.4.1 – Задана рама
Будуємо одиничні та вантажну епюри моментів (рис. 2.4.3):

Рисунок 2.4.3 – Одиничні та вантажна епюри моментів
Обчислюємо коефіцієнти та вільні члени системи канонічних рівнянь
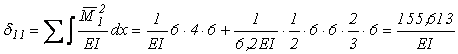 ;
;
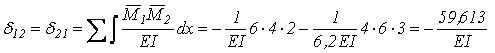 ;
;
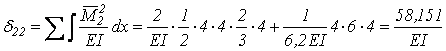 ;
;
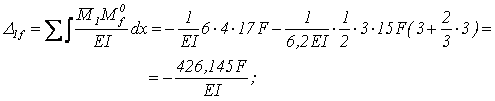
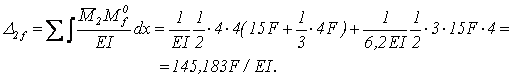
Розв’язуючи систему канонічних рівнянь, знаходимо невідомі X1 та X2
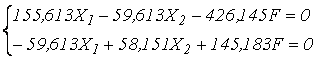
Будуєм о епюру пружних моментів для заданої рами (рис. 2.4.4)
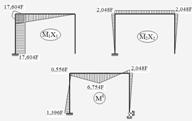
Рисунок 2.4.4 – Побудова пружної епюри моментів першого етапу
В. 8. Прирівнюємо максимальні моменти в ригелі і в стояку до відповідних граничних моментів.
Переріз 4: 6,754F=335,20; ![]() F=335,20/6,754=49,630 кН.
F=335,20/6,754=49,630 кН.
Переріз 6: 2,048F= 95,52; ![]() F=95,52/2,048=46,641 кН.
F=95,52/2,048=46,641 кН.
9. За граничне приймаємо найменше з одержаних навантажень
![]() кН. Пластичний шарнір утворюється в перерізі 6.
кН. Пластичний шарнір утворюється в перерізі 6.
10. Будуємо епюру граничних моментів першого етапу розрахунку (рис. 2.4.5)
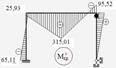
Рисунок 2.4.5 – Гранична епюра моментів першого етапу розрахунку
Другий етап розрахунку.
Г. 11, 12. Будуємо розрахункову схему рами (рис. 2.4.6, а) і основна система методу сил (рис. 2.4.6, б).
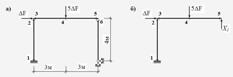
Рисунок 2.4.6 – Розрахункова схема рами (а) і основна система методу сил (б)
Записуємо канонічне рівняння методу сил
Будуємо одиничну та вантажну епюри моментів.
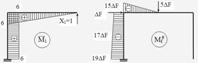
Рисунок 2.4.7 – Одинична та вантажна епюри моментів
Обчислюємо одиничне та вантажне переміщення.
Оскільки одинична та вантажна епюри моментів другого етапу розрахунку збігаються з відповідними епюрами першого етапу, то числові значення переміщень беремо з першого етапу розрахунку:
Розв'язуємо рівняння: ![]() ;
;
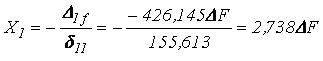 .
.Будуємо епюру пружних згинальних моментів II етапу розрахунку (рис. 2.4.8)
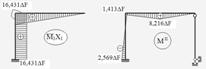
Рисунок 2.4.8 – Побудова пружної епюри моментів ІІ етапу
Д. 13. Обчислюємо приріст граничного навантаження
Приріст параметра навантаження, що відповідає утворенню другого пластичного шарніра, визначається за допомогою залежності
Переріз 1:
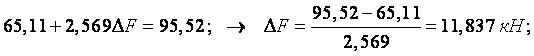
Переріз 2:
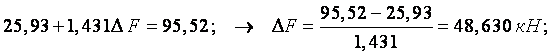
Переріз 4:
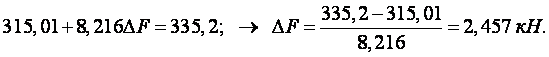
14. Найменше значення ![]() одержано для перерізу 4. Таким чином, приріст параметра граничного навантаження:
одержано для перерізу 4. Таким чином, приріст параметра граничного навантаження: ![]() кН. Пластичний шарнір утвориться в перетині 4.
кН. Пластичний шарнір утвориться в перетині 4.
15. Параметр граничного навантаження другого етапу розрахунку
16. Епюра граничних моментів II етапу розрахунку (рис. 2.4.9)
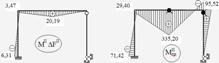
Рисунок 2.4.9 – Побудова епюри граничних моментів ІІ етапу розрахунку
Третій етап розрахунку
Е. 17, 18. Будуємо розрахункову схему рами (рис. 2.4.10, а) і епюру „пружних” моментів IІІ етапу розрахунку (рис. 2.4.10, б).
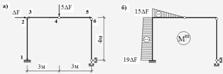
Рисунок 2.4.10 – Розрахункова схема (а) і епюра пружних моментів (б)
Ж. 19. Обчислюємо приріст граничного навантаження на основі аналізу епюр ![]() та
та ![]() .
.
Переріз 1: 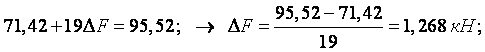
Переріз 2: 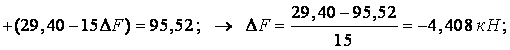
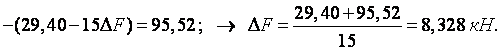
20. Оскільки приріст навантаження не може бути від'ємним, то
Пластичний шарнір утворюється в перерізі 1.
21. Остаточне значення параметра граничного навантаження для заданої рами
22. Остаточна епюра граничних згинальних моментів для заданої рами (рис. 2.4.11).
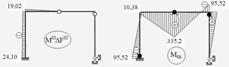
Рисунок 2.4.11 – Побудова остаточної граничної епюри моментів
И. 23. Будуємо пластичний механізм руйнування рами (рис. 2.4.12).
Тип механізму руйнування рами - комбінований: балочний з боковим зміщенням.
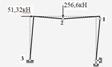
Рисунок 2.4.12 – Пластичний механізм руйнування рами
З. 24. Будуємо епюру „пружних” згинальних моментів при дії граничного навантаження ![]() і епюру залишкових згинальних моментів (рис. 2.4.13)
і епюру залишкових згинальних моментів (рис. 2.4.13)
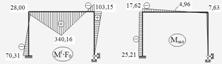
Рисунок 2.4.13 – Побудова залишкової епюри моментів
Оскільки залишкові моменти діють в рамі після зняття навантаження і є результатом пластичного деформування, то епюра залишкових моментів повинна бути лінійною в кожному стержні рами. В даному випадку перевіряємо це твердження для ригеля рами.
Середня лінія трапеції (7,63-17,62)/2 = -4,995, що не збігається з відповідною ординатою на епюрі залишкових моментів. Похибка складає:
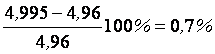 .
.

