А. 1. Виражаємо діючі навантаження через параметр F.

Використовуючи співвідношення  приймаємо:

,   або  .

2. Визначаємо ступінь статичної невизначеності заданої рами

.

3. Підраховуємо число пластичних шарнірів, що необхідні для утворення повного пластичного механізму руйнування рами

.

4. Визначаємо число розрахункових перерізів “s”, тобто число перерізів рами, в яких слід обчислити згинальні моменти для побудови епюри М.

5. Для залізобетонних прямокутних перерізів ригеля і стояків рами з арматурою в розтягнутих зонах бетону обчислюємо граничні згинальні моменти:

,        ,

де  - площа поперечного перерізу залізобетонного стержня; 

 - розрахунковий опір бетону;

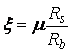 - відносна висота стиснутої зони бетону;

 - коефіцієнт армування; 

 - площа та розрахунковий опір розтягнутої арматури (для арматури класу  кН/м²).

Б. 6. Записуємо  нерівностей, що виражають умови текучості

       .

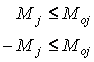
6. Записуємо  рівнянь рівноваги вузлів та частин рами

.

При формуванні рівнянь рівноваги згинальні моменти та поперечні сили прикладаємо так, щоб вони були додатні. Поперечні сили виражаємо через згинальні моменти                         .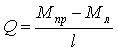

8. Записуємо систему рівнянь та нерівностей, що виражають умови статичної теореми

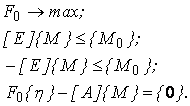
де  – параметр граничного навантаження; 

 – вектор, що визначає в відносних величинах розподіл зовнішнього навантаження;

 – одинична матриця;  {M} – вектор згинальних моментів в перерізах рами в граничному стані;   

[A] – матриця коефіцієнтів рівнянь рівноваги.

9. Розв’язуємо за допомогою EXCEL записану задачу лінійного програмування і одержуємо параметр граничного навантаження  та вектор згинальних моментів в розрахункових перерізах рами {M}.

10. Будуємо граничну епюру згинальних моментів.

В. 11. Записуємо систему рівнянь та нерівностей, що виражають умови кінематичної теореми

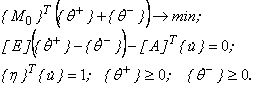
де ,  – вектори швидкостей пластичних деформацій, що   задовольняють умові ; 

 – вектор швидкості переміщень;  верхній індекс "Т" означає операцію транспонування матриці чи вектора.

12. Знаходимо параметр граничного навантаження  і вектор швидкостей пластичних деформацій та переміщень, розв’язуючи за допомогою EXCEL записану задачу лінійного програмування.

13. Будуємо пластичний механізм руйнування рами.