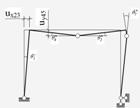
2.4 Розрахунок несучої здатності статично невизначеної рами з урахуванням пластичної роботи матеріалу
2.4.3 Розрахунок несучої здатності рами з використанням статичної та кінематичної теорем
2.4.3.3 Приклад розрахунку
2.4.3 Розрахунок несучої здатності рами з використанням статичної та кінематичної теорем
2.4.3.3 Приклад розрахунку

Розрахунок
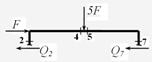
A. 1. Виражаємо діюче навантаження через параметр F: F1=5F, F2=F.
2. Ступінь статичної невизначеності рами n=5+2×0 - 3×1=2.
3. Число пластичних шарнірів, необхідних для утворення повного пластичного механізму руйнування рами k=2+1=3.
4. Число розрахункових перерізів рами s= 7.
5. Граничні згинальні моменти для ригеля і стояків


Б. 6. Записуємо 2∙7=14 нерівностей, що виражають умови текучості
7. Записуємо 7–2=5 рівнянь рівноваги, з яких 3 рівняння являють собою умови рівноваги вузлів - ![]() :
:
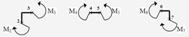
Ще два рівняння рівноваги одержимо, записуючи умови рівноваги частин рами
Зважаючи на те, що
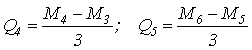 ,
,одержимо:
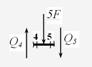
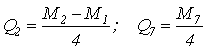 .
.
8. Записуємо систему рівнянь та нерівностей, що виражають собою
статичну теорему. Невідомі – параметр граничного навантаження ![]() і моменти
і моменти ![]() в перерізах рами.
в перерізах рами.
9. Розв’язуємо задачу лінійного програмування, скориставшись програмою Microsoft Excel.
В клітинках K1 та K2 записуємо числові значення граничних моментів для стояків та ригеля рами. Коефіцієнти системи нерівностей та рівнянь записуємо в клітинках A4:H22. В клітинках А24:Н24, куди перед розрахунком заносяться довільні значення (наприклад, одиниці), одержимо розв'язок задачі лінійного програмування. В клітинки І4:І23 записуємо результат перемноження матриці коефіцієнтів системи нерівностей та рівнянь на вектор, записаний в клітинках А24:Н24. Наприклад, в клітинці І22 потрібно записати:


В стовпці J4:J23 записані умови, які повинні задовольняти система нерівностей та рівнянь. Це текстові дані, записані тільки для наочності і в розв'язуванні не використовуються.
В клітинці І23 одержимо значення цільової функції (параметр граничного навантаження).
Після заповнення таблиці відкриваємо меню "Сервис", вибираємо пункт "Поиск решения" і заповнюємо необхідні параметри. Встановлюємо цільову клітинку І23, де записана цільова функція, і вказуємо, що відшуковується максимальне значення цільової функції. Клітинки, що змінюються в процесі розв'язку задачі – А24:Н24, містять значення невідомих. Обмеження задачі заносимо, вибравши кнопку "Добавить".

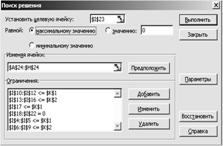
Після занесення всіх необхідних даних вибираємо кнопку "Выполнить" і в клітинках А24:Н24 одержуємо розв'язок задачі – параметр граничного навантаження і згинальні моменти в перерізах рами.

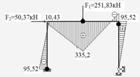
10. Будуємо граничну епюру згинальних моментів. Пластичні шарніри виникають в перерізах 1, 4, 5, 7, де згинальні моменти досягають граничних величин
В. 11. Записуємо систему рівнянь і нерівностей кінематичної теореми. Невідомими, що відшуковуються, є параметр граничного навантаження ![]() , швидкості кутових пластичних деформацій
, швидкості кутових пластичних деформацій ![]() і швидкості пластичних переміщень (кутових та лінійних)
і швидкості пластичних переміщень (кутових та лінійних) ![]() . Відповідна таблиця EXCEL подана на рисунку. Матриця коефіцієнтів, що записана за адресою A4:S11, одержана шляхом транспонування матриці коефіцієнтів статичної теореми (A4:H22). В клітинках А12:N12 записані значення граничних моментів в розрахункових перерізах рами. В клітинках A13:S13 записані попередні (довільні) значення невідомих швидкостей деформацій та переміщень. В стовпці Т4:Т12 записано результати перемноження значень рядка 13 на відповідний рядок матриці коефіцієнтів. Наприклад, в клітині Т5 записано: =A13*A5+H13*H5+S13*S5. В стовпці U4:U12 записані умови задачі.
. Відповідна таблиця EXCEL подана на рисунку. Матриця коефіцієнтів, що записана за адресою A4:S11, одержана шляхом транспонування матриці коефіцієнтів статичної теореми (A4:H22). В клітинках А12:N12 записані значення граничних моментів в розрахункових перерізах рами. В клітинках A13:S13 записані попередні (довільні) значення невідомих швидкостей деформацій та переміщень. В стовпці Т4:Т12 записано результати перемноження значень рядка 13 на відповідний рядок матриці коефіцієнтів. Наприклад, в клітині Т5 записано: =A13*A5+H13*H5+S13*S5. В стовпці U4:U12 записані умови задачі.

Після формування таблиці відкриваємо меню "Сервис", вибираємо пункт "Поиск решения" і заповнюємо необхідні параметри. Встановлюємо цільову клітину Т12, де записана цільова функція, і вказуємо, що відшуковується мінімальне значення цільової функції. Клітинки, що змінюються в процесі розв'язування задачі – А13:S13, містять значення невідомих. Обмеження задачі заносимо, вибравши кнопку "Добавить".
Після занесення всіх необхідних даних вибираємо кнопку "Выполнить" і в клітинках А13:S13 одержуємо розв'язок задачі – параметр граничного навантаження і швидкості пластичних деформацій та переміщень.
Параметри граничного навантаження, одержані за допомогою статичної та кінематичної теорем збігаються. Це свідчить про те, що задача розв’язана правильно. Пластичні шарніри утворюються в 1, 5 і 7 перерізах рами – там, де швидкість пластичних деформацій відмінна від нуля.

Утворення трьох пластичних шарнірів означає, що реалізується повний пластичний механізм руйнування рами.