2.7 Динамічний розрахунок статично невизначеної рами за методом сил на дію гармонійного навантаження
2.7.2 Приклад розрахунку
2.7.2 Приклад розрахунку
Розрахункова схема (рис. 2.7.1) і вихідні дані:
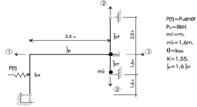
Рисунок 2.7.1 – Розрахункова схема та напрями коливань точкових мас
Ступінь статичної невизначеності: L= 2Ш + С0 - 3D =1.
Число динамічних ступенів вільності (рис. 2.7.1):
(1) - перший можливий напрям коливань маси ![]()
(2) - другий можливий напрям коливань маси ![]()
Отже, число динамічних ступенів вільності рівне двом.
За методом сил розраховуємо епюри згинальних моментів від окремо діючих одиничних інерційних сил і збурювальної сили одиничної величини:
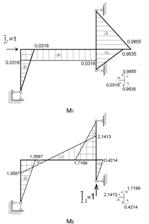
Рисунок 2.7.2 – Епюри моментів у статично невизначеній рамі від дії одиничних інерційних сил I1=1, I2=1 (після розкриття статичної невизначеності за методом сил)
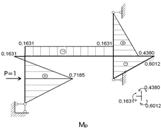
Рисунок 2.7.3 – Епюра моментів в статично невизначеній рамі від дії одиничного зовнішнього навантаження (після розкриття статичної невизначеності за методом сил)
Запис вікового рівняння:
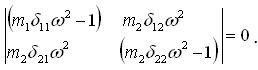 . . |
(2.7.1) |
Коефіцієнти вікового рівняння:
ЕJδ11 = М1∙М1 = 1,2975;
ЕJδ22 = М2∙М2 = 7,0968;
ЕJδ12 = ЕJδ21 = М1∙М2 = -1,1793;
ЕJδ1р = М1∙Мр = 0,6689;
ЕJδ2р = М2∙Мр = 0,2801.
Частоти власних коливань (freefluctuations) обчислюються за формулою:
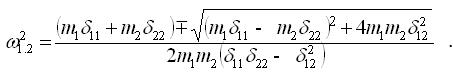 |
(2.7.2) |
Після підстановки коефіцієнтів δij отримаємо:
Перевірка властивостей власних чисел за формулою
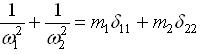 . . |
(2.7.3) |
Після підстановки коефіцієнтів отримаємо:
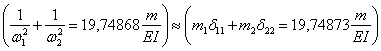 .
.Коефіцієнти головних форм коливань обчислюються за формулами
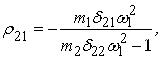
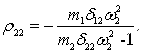
Після обчислень одержуємо:
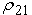 = -5,6566;
= -5,6566; 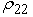 = 0,06792.
= 0,06792.Перевірка ортогональності головних форм коливань за відомими їх коефіцієнтами за рівністю:
| m1+m2р21р22=0, | (2.7.4) |
яка після підстановки коефіцієнтів приводить до тотожності:
Побудова головних форм коливань виконується за допомогою коефіцієнтів ![]() , для цього у напрямі першого коливання відкладається амплітуда, рівна одиниці (в довільному масштабі). Для викреслювання першої головної форми коливань необхідно відкласти амплітуду за напрямом другого коливання, рівну коефіцієнту
, для цього у напрямі першого коливання відкладається амплітуда, рівна одиниці (в довільному масштабі). Для викреслювання першої головної форми коливань необхідно відкласти амплітуду за напрямом другого коливання, рівну коефіцієнту ![]() , а для отримання другої головної форми коливань необхідно відкласти за напрямом другого коливання амплітуду, рівну коефіцієнту
, а для отримання другої головної форми коливань необхідно відкласти за напрямом другого коливання амплітуду, рівну коефіцієнту ![]() . Деформований стан рами викреслюється з дотриманням таких правил: прямі жорсткі вузли рами до деформації залишаються прямими і після деформації; на першій головній формі коливань не повинно бути точок перегину пружних осей ригелів і стояків; на другій головній формі коливань можлива поява однієї точки перегину.
. Деформований стан рами викреслюється з дотриманням таких правил: прямі жорсткі вузли рами до деформації залишаються прямими і після деформації; на першій головній формі коливань не повинно бути точок перегину пружних осей ригелів і стояків; на другій головній формі коливань можлива поява однієї точки перегину.
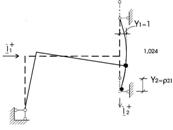
Рисунок 2.7.4 – Перша головна форма коливань
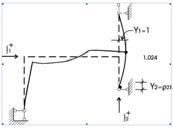
Рисунок 2.7.5 – Друга головна форма коливань
Система амплітудних рівнянь рівноваги Безухова:
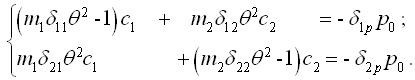 |
(2.7.5) |
Побудова і розрахунок графіків розвитку амплітуд вимушених коливань проводиться за такими формулами:
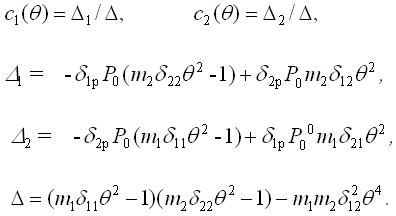 |
(2.7.6) |
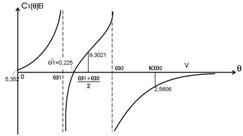
Рисунок 2.7.6 – Графік розвитку амплітуди за напрямом першої
форми коливання
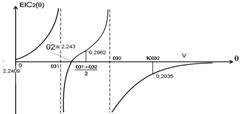
Рисунок 2.7.7 – Графік розвитку амплітуди за напрямом другої форми коливання
Графіки розвитку динамічних коефіцієнтів розраховують за формулами:
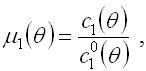 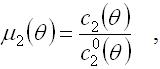 |
(2.7.7) |
де ![]() – амплітуди вимушених коливань відповідно за першим і другим напрямами при заданій частоті q;
– амплітуди вимушених коливань відповідно за першим і другим напрямами при заданій частоті q;
![]() – переміщення мас, які коливаються відповідно за першим і другим напрямами, викликані статичною дією збурювальної сили Р.
– переміщення мас, які коливаються відповідно за першим і другим напрямами, викликані статичною дією збурювальної сили Р.
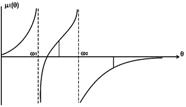
Рисунок 2.7.8 – Графік розвитку першого динамічного коефіцієнта
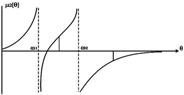
Рисунок 2.7.9 – Графік розвитку другого динамічного коефіцієнта
Частоти віброгасіння обчислюємо за формулами:
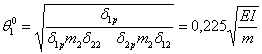 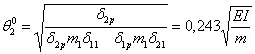 |
(2.7.8) |
Інерційні сили розраховуємо для частоти збурювальної сили, заданої в початкових даних:
При цьому:
а) інерційна сила за напрямом першого коливання:
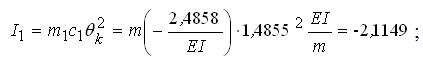 ;
;
б) інерційна сила за напрямом другого коливання:
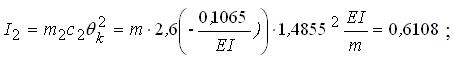 ;
;
Динамічна епюра згинальних моментів:
| Мдин = Мр+М1∙I1+ М2∙I2, | (2.7.9) |
яка остаточно має такий вигляд:
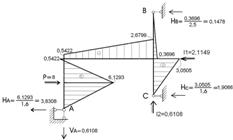
Рисунок 2.7.10 – Кінцева динамічна епюра згинальних моментів Мдин
Для перевірки динамічної епюри згинальних моментів необхідно обчислити за величинами ординат моментів реакції в опорних стержнях (Мдин) і вимагати виконання рівнянь статики:
а) вузли рами повинні перебувати в рівновазі:

![]() ;
;
б) сума проекцій на горизонтальну вісь:
в) сума проекцій всіх сил на вертикальну вісь:


