ПОДВІЙНОЇ КРИВИЗНИ
3.1 Загальні відомості про оболонки
3.1.1 Означення
3.1.1 Означення
Оболонка – це тіло, один з розмірів якого (товщина) значно менший, ніж два інші лінійні розміри. Поверхня, що проходить через точки, розташовані посередині товщини оболонки, називається серединною поверхнею оболонки. В оболонках постійної товщини геометрія серединної поверхні визначає геометрію оболонки в цілому (рис. 3.1.2).
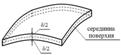
Рисунок 3.1.2 – Елемент оболонки постійної товщини
В подальшому будемо розглядати так звані тонкі оболонки. Тонкою будемо називати таку оболонку, для якої виконується умова
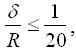
де R – радіус кривизни серединної поверхні;
δ – товщина оболонки.
Якщо ця умова не виконується, оболонка вважається товстою. Для розв’язування задачі про згинання кожної із зазначених груп оболонок застосовують відповідну теорію.
Більшість реальних оболонок мають товщину, що розташована в діапазоні
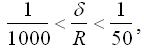
тобто належать до класу тонких оболонок. Саме тому теорія тонких оболонок має найбільше практичне застосування.
Надалі розглядатимемо класичну теорію тонких оболонок [10, 19, 23], які широко застосовуються в будівництві. Теорія придатна, якщо прогини оболонки не перевищують 1/5 її товщини. Такі оболонки називаються жорсткими. В разі більших прогинів застосовують теорію гнучких оболонок. Класична теорія тонких оболонок, що є наближеною, ґрунтується на гіпотезах Кірхгофа.


