 |
|---|
11 ГРАНИЧНИЙ ШАР НЕСТИСЛИВОЇ РІДИНИ
Основні поняття і залежності
В сучасних умовах широко використовується «зшивка» рішень: характеристики ядра потоку знаходяться із розв’язання задачі потенціальної течії, а для врахування особливостей пристінного руху застосовується теорія прикордонного шару. Одна із найбільш важливіших практичних задач механіки рідини та газу – це визначення опору. На величину відповідного коефіцієнту опору, в основному, впливає гідродинамічна обстановка в безпосередній близькості від твердої межі потоку, в так званому граничному шарі. Оскільки розрахувати деталі течії в цій області на основі розв’язання рівнянь Навьє-Стокса не представляється можливим в силу нелінійності і складності останніх, то виникає необхідність в якихось задовільних наближеннях, одним із котрих є теорія граничного шару.
Німецький інженер і математик Л. Прандтль в 1904 році опублікував теорію граничного шару. Це велике відкриття в історії механіки рідини, воно дозволило зрозуміти багато уявних парадоксів в поводженні реальної рідини.11.1 Види і структура граничного шару
На пластину натікає потік газу зі сталою швидкістю(рис. 11.1)
Нема відриву струмини, але вздовж пластинки виникає так званий граничний шар (ГШ) рідини, поперечні розміри d котрого збільшуються вниз по течії. Поза цим шаром швидкість потоку така, якою вона була б при відсутності пластинки, тобто вплив в’язкості тут може бути знехтуваним. Навпаки, в межах граничного шару сили в’язкості виявляються настільки суттєвими, як і сили інерції.
ГШ починається у передній точці обтікаємого тіла, розповсюджуючись по всій його поверхні; при цьому він поступово розширюється. Практично за товщину шару приймають ту відстань від пластинки, де швидкість відрізняється не більш ніж на 1% від швидкості незбуреного потоку(рис. 11.1).
ГШ може бути ламінарним або турбулентним. Від стану ГШ в значній мірі залежить і величина опору тертя,
. (11.1)
Для плоскої пластинки ламінарний граничний шар переходить в турбулентний при
. (11.2)
де хкр – довжина від переднього ребра пластинки до кінця ламінарної частини граничного шару. Якщо L <, то весь граничний шар буде ламінарним; при L >
– частина граничного шару буде ламінарною, а частина – турбулентною (змішаний граничний шар).
Опір пластинки в потоці при обтіканні її вздовж
При визначенні величини опору тертя застосовується залежність
, (11.3)
де w – площа обтікаємої поверхні тіла;
– коефіцієнт опору тертя.
Розглянемо пластинку довжиною L, шириною l, площею, яку обтікає потік рідини. Виділяємо перерізи 1 та 2.
Застосуємо теорему про кількість руху. Різниця кількості руху рідини, яка протікає в одиницю часу через вказані перерізи, повинна дорівнювати сумі всіх сил, які діють на рідину на ділянці довжиною х між перерізами 1 і 2.
Розглянемо елементарну площадку 1dy другого перерізу потоку. Маса рідини, яка протікає через цю площадку –– об’єм рідини, яка проходить через площадку в одиницю часу. Втрата швидкості, яка визвана гальмуючою дією пластинки, дорівнює u? - u. Таким чином зменшення кількості руху за рахунок сил тертя
. (11.4)
Втрата кількості руху торкається тільки тих частинок, котрі знаходяться всередині граничного шару, для всієї останньої маси рідини u =, отже,
. Тому шукана різниця кількості руху рідини, яка протікає в одиницю часу через перший і другій переріз потоку, виразиться інтегралом
, (11.5)
який розповсюджений тільки в межах граничного шару і при тому по обидві сторони пластинки (це враховується множником 2).
Опір тертя тої частини пластинки, котра заключна між перерізами 1 і 2
, (11.6)
де– напруження тертя на довільному елементі поверхні.
У відповідності з теоремою імпульсів
(11.7)
або
(11.8)
Диференцюючи обидві частини останнього виразу по x, отримаємо
(11.9)
Рівняння (11.9) представляє собою спрощену форму так званого інтегрального співвідношення Кармана, справедливого як при ламінарному так і турбулентному режимах.
При ламінарному обтіканні пластини наближено приймемо лінійний закон розприділення швидкостей
. (11.10)
Згідно закону Н’ютона, дотичні напруження на стінці
(11.11)
Визначимо тепер значення інтегралу, який входить в ліву частину рівняння (11.9)
. (11.12)
Підставимо (11.12) в (11.9)
(11.13)
або з врахуванням (11.11)
(11.14)
Відповідно товщина граничного шару, дотичне напруження на відстані х від переднього ребра платини
(11.15)
(11.16)
Повний опір тертя пластинки довжиною L з обох боків
(11.17)
Коефіцієнт опору тертя
(11.18)
де
Проведений Блазіусом більш точний розрахунок дозволив отримати таку залежність
(11.19)
У випадоку турбулентного обтікання можна використати дані, які отримані при досліджені турбулентного руху рідини в трубі діаметром d
(11.20)
де V – середня швидкість потоку в трубі;
(11.21)
Рівнянням (11.21 ) можна користуватися для оцінки опору тертя, яке відбувається у поверхні пластинки. Переходимо з середньої швидкості в трубі V до швидкості на вісі труби– товщина граничного шару, а r – радіус труби, тоді
(11.22)
Приймаємо розподіл швидкості в граничному шарі
(11.23)
Тоді відповідно товщина граничного шару, дотичне напруження на відстані х від переднього ребра пластини
(11.24)
(11.25)
Опір тертя пластинки довжиною L і шириною 1 м при односторонньому обтіканні
(11.26)
Коефіцієнт тертя
(11.27 )
де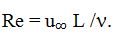
Узагальнена формула Альтшуля (11.27) для коефіцієнта опору тертя пластинки дійсна для всієї області турбулентної течії.
На випадок, коли
(11.28)
що характерно для обтікання моделей (мала шорсткуватість поверхні, малі швидкості ) рівняння (11.27 ) приймає вигляд
- одностороннє обтікання:
(11.29)
На випадок, коли
(11.30)
що характерно для великих швидкостей і значної шорсткості, рівняння приймає вигляд
(11.31)
Більш строга залежність при умовах (11.28 )
(11.32)
при умовах (11.30 )
(11.33 )