 |
|---|
10 ОДНОМІРНІ ТЕЧІЇ ГАЗУ
10.1 Рівняння Бернуллі для адіабатної течії газу, швидкість звуку, максимальна і критична швидкість, критичні параметри
Для одномірних потоків характерна зміна всіх параметрів тільки в одному напрямку. Наприклад, швидкість С, тиск Р, густина
температура Т залежать від однієї координати l і часу
.
Ці обставини суттєво спрощують всі вихідні рівняння і дозволяють врахувати і проаналізувати вплив різних зовнішніх дій на структуру потоку.
Одномірною можна вважати течію рідини в каналі з поперечним перерізом, що плавно змінюється і малою кривизною вісі. Одночасно вводиться припущення про сталість всіх параметрів потоку в поперечному перерізі каналів або замість дійсних величин використовуються їх середні значення.
Ця наближена модель потоку в багатьох випадках достатньо добре співпадає з експериментом.
Рівняння безперервності для двох довільних перерізів 1 і 2 при відсутності масообміну з зовнішнім середовищем, приймає вигляд
. (10.1)
Логарифмуючи вираз (10.1) одержимо
. (10.2)
А логарифмічний диференціал від (10.1) має вигляд
. (10.3)
При цьому враховані такі перетворення
(10.4)
Рівняння кількості руху для одномірної сталої, енергоізольованої течії при відсутності масових сил безпосередньо витікає із рівняння Ейлера
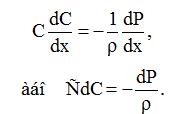
(10.5)
Його інтегралом є рівняння Бернуллі для баротропної рідини
(10.6)
Ізоентропійний (адіабатний)процес описується залежностями
. (10.7)
Рівняння енергії (теплоємності) для ідеальної рідини, що стискається, має такий же вигляд для ізоентропійного як і рівняння кількості руху
(10.8)
Параметри гальмування
Записуючи (10.8) для перерізу, де швидкість зменшується до нуля і, отже, потік гальмується, знайдемо вираз для сталой в правій частині (10.8). Ця стала може бути представлена різними способами
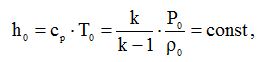
(10.9)
де h0 – ентальпія загальмованого потоку або його повна енергія;
– параметри загальмованого потоку або параметри повного гальмування.
При повному гальмуванні потоку вся кінетична енергія переходить в теплову і температура Т0, також як і ентальпія, має одне визначене значення. Тиск гальмування Р0 і густинаможуть приймати різні значення, але їх відношення
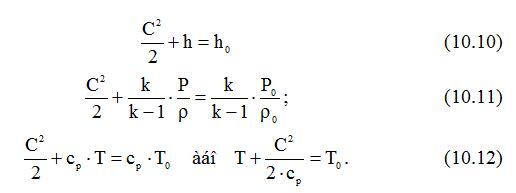
Як видно із (10.10) – (10.12), в сталому енергоізольованому потоці сума кінетичної і потенціальної енергії (віднесеної до одиниці маси) стала вздовж трубки току.
Якщо газовий струмінь загальмувати цілком, то параметри газу досягають максимального значення. При ідеальному гальмуванні газового потоку перехід від стану руху до загальмованого стану описується рівнянням ідеальної адіабати
(10.13)
де k – показник адіабати.
Швидкість звуку
Під швидкістю звуку а розуміють швидкість розповсюдження малих збурювань. Дозвукова течія реалізується при с< а, надзвукова – с> а.
Є принципова різниця в поведінці дозвукових і надзвукових потоків. Оцінка тієї межі швидкостей, де ще можливо вважати рідини нестисливими і не враховувати в розрахунках зміну їх густини, дуже важлива.
Правильна оцінка швидкості звуку дозволяє визначати не тільки методи розв’язання газодинамічних задач, але й правильність кінцевих результатів.
В однофазному ізоентропійному потоцішвидкість розповсюдження слабих збурювань (швидкість звуку) залежить від фізичних властивостей середовища, його температури і визначається за допомогою залежностей
(10.14)
Критична швидкість
Із аналізу рівнянь (10.10) – (10.12) – швидкість потоку не може рости нескінченно, а обмежується деякою максимальною величиноюВона досягається при повному переході всієї наявної енергії в кінетичну.
Отже, із (10.10) – (10.12)
(10.15)
Оскільки швидкість звуку визначається за залежностями (10.14), а для загальмованого потоку
. (10.16)
Перетворимо (10.11) до вигляду
. (10.17)
Звідсіля
. (10.18)
Фізично максимальна швидкість відповідає витіканню газу в абсолютний вакуум (h = 0, P = 0, T = 0). Практично така швидкість недосяжна. Таким чином, максимальна швидкість є теоретичною межею для швидкості газу.
Використовуючи (10.18) запишемо (10.17) у вигляді
(10.19)
Переріз хкр (тут С = а = С*) і параметри в цьому перерізі назвемо критичними(див. рис. 10.1).
Дуже важливе значення в газодинамічних дослідженнях мають безрозмірні швидкості :
– число Маха – це відношення швидкості потоку до швидкості звуку в даному газовому потоці; дає співвідношення між кінетичною і потенційною енергією потоку;
– коефіцієнт швидкості газового потоку.
Якщо М < 1, то плин називається дозвуковим.
Якщо М > 1 – надзвуковий плин газу.
Якщо М = 1 – критичний плин.
Параметри потоку при числі Маха М=1 називаються критичними параметрами
Критична швидкість
. (10.20)
Критична температура
. (10.21)
Рівняння теплоємності можна записати в безрозмірному вигляді
(10.22)
При надзвуковому плині газу або при русі твердого тіла в газі з надзвуковою швидкістю виникають ударні хвилі або стрибки ущільнень. Швидкість у прямому стрибку падає, при цьому надзвукова швидкість до стрибка переходить у дозвукову швидкість після стрибка. Зв’язок швидкостей визначається за формулою
. (10.23)
Тиск у прямому стрибку збільшується. Відношення тисків можна виразити
. (10.24)
Швидкість витікання у вихідному перетині сопла, що звужується, визначається за формулою
. (10.25)
Масова витрата через сопло визначається за формулою
. (10.26)
Плин газу в соплі характеризується двома безрозмірними параметрами: коефіцієнтом тиску, коефіцієнтом швидкості
.
