
І.І.Ваганов, І.В.Маєвська, М.М.Попович
РОЗРАХУНОК ОСНОВ І ФУНДАМЕНТІВ НА ЕОМ
Курсове та дипломне проектування
1 Загальні положення з розрахунку і проектування основ і фундаментів
2 Підготовка даних для проектування основ та фундаментів
3 Розрахунок та проектування фундаментів мілкого закладання
4 Розрахунок пальових фундаментів
5 Розрахунок деформацій основ
6 Перевірка слабкого підстилкового шару і проектування ґрунтових подушок
Література
2 ПІДГОТОВКА ДАНИХ ДЛЯ ПРОЕКТУВАННЯ ОСНОВ ТА ФУНДАМЕНТІВ
2.2 Визначення нормативних та розрахункових значень характеристик ґрунтів
2.2.1 Методика розрахунків
Нормативні та розрахункові значення характеристик ґрунтів обчислюють за результатами безпосередніх визначень для кожного інженерно-геологічного елемента будівельного майданчика, а для характеристик міцності та деформаційних характеристик - як за результатами безпосередніх визначень, так і з використанням таблиць, де вони визначаються за фізичними властивостями.
Статистичну обробку дослідних даних починають із перевірки на вилучення грубих помилок - відскоків. Для цього визначають середнє арифметичне значення характеристики
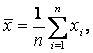 (2.1)
(2.1)
де хi - часткове значення характеристики,
n - число її визначень.
Вилучати треба максимальні або мінімальні часткові значення, для яких виконується умова
![]() , (2.2)
, (2.2)
де n - статистичний критерій, який приймається в залежності від кількості визначень (табл.2.1);
Таблиця 2.1 - Значення статистичного критерію
Число визначень |
n |
Число визначень |
n |
Число визначень |
n |
6 |
2,07 |
13 |
2,56 |
20 |
2,78 |
7 |
2,18 |
14 |
2,60 |
25 |
2,88 |
8 |
2,27 |
15 |
2,64 |
30 |
2,96 |
9 |
2,35 |
16 |
2,67 |
35 |
3,02 |
10 |
2,41 |
17 |
2,70 |
40 |
3,07 |
11 |
2,47 |
18 |
2,73 |
45 |
3,12 |
12 |
2,52 |
19 |
2,75 |
50 |
3,16 |
Sdis - зміщена оцінка середнього квадратичного відхилення характеристики, яка обчислюється за формулою
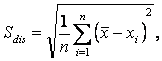 (2.3)
(2.3)
Якщо грубі помилки вилучені, то нормативне значення ( ) обчислюють за формулою (2.1). При їх відсутності за нормативне приймають середнє арифметичне значення тієї чи іншої характеристики.
Нормативне значення механічних характеристик ґрунтів - кута внутрішнього тертя, φ, та питомого зчеплення, С, обчислюють методом найменших квадратів для усієї сукупності дослідних даних за нормативною залежністю
t = s tg j + c, (2.4)
де t - граничне напруження зсуву (зрізу), кПа;
s - нормальне напруження стиску, кПа.
Перевірку та вилучення грубих помилок у значеннях характеристик виконують для кожного значення нормальних напружень окремо.
Обчислення здійснюють за формулами:
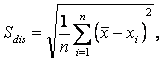 (2.5)
(2.5)
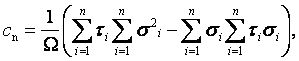 (2.6)
(2.6)
або
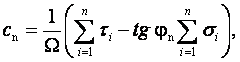 (2.7)
(2.7)
де
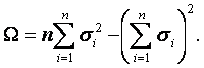 (2.8)
(2.8)
Середнє квадратичне відхилення для усіх характеристик ґрунтів, крім c і j, обчислюють за формулою
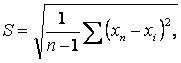 (2.9)
(2.9)
Для c і j:
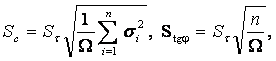 (2.10)
(2.10)
де
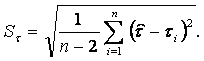 (2.11)
(2.11)
У формулі (2.11) значення обчислюють за формулою (2.4) для кожного значення нормальних напружень і нормативних значень c і j.
Визначають коефіцієнт варіації
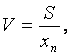 (2.12)
(2.12)
помилку середнього значення Dx (в абсолютних одиницях) або dx (відносну помилку):
![]() (2.13)
(2.13)
Довірчий інтервал, що характеризує зону навколо середнього значення, в межах якої із заданою ймовірністю a знаходиться істинне генеральне середнє значення для цих характеристик (крім c і j), обчислюють за формулами:
![]() (2.14)
(2.14)
Для с і j:
![]() (2.15)
(2.15)
де ta - статистичний коефіцієнт, який визначається в залежності від заданої ймовірності (надійності) a та числа визначень n (табл.2.2).
Довірча ймовірність приймається при розрахунках за І групою граничних станів a = 0,95 , за II групою - 0,85.
Усі розрахунки основ повинні виконуватись з використанням розрахункових характеристик х, які обчислюються за формулою
![]() (2.16)
(2.16)
де gg - коефіцієнт надійності за ґрунтом:
![]() (2.17)
(2.17)
Порівнюючи формули (2.16) та (2.17), знаходимо, що
х = xn(1 ± d) або х = xn ± D. (2.18)
Таблиця 2.2 - Значення коефіцієнта tα при односторонній довірчій ймовірності α
Число визначень n-1 для Rc і n-2 для c і j |
ta при a |
Число визначень n-1 або n-2 |
ta при a |
|||
0,85 |
0,95 |
0,85 |
0,95 |
|||
2 |
1,34 |
2,92 |
13 |
1,08 |
1,77 |
|
3 |
1,25 |
2,35 |
14 |
1,08 |
1,76 |
|
4 |
1,19 |
2,13 |
15 |
1,07 |
1,75 |
|
5 |
1,16 |
2,01 |
16 |
1,07 |
1,75 |
|
6 |
1,13 |
1,94 |
17 |
1,07 |
1,74 |
|
7 |
1,12 |
1,90 |
18 |
1,07 |
1,73 |
|
8 |
1,11 |
1,86 |
19 |
1,07 |
1,73 |
|
9 |
1,10 |
1,83 |
20 |
1,06 |
1,72 |
|
10 |
1,10 |
1,81 |
30 |
1,05 |
1,70 |
|
11 |
1,09 |
1,80 |
40 |
1,05 |
1,68 |
|
12 |
1,08 |
1,78 |
60 |
1,05 |
1,67 |
|
В формулах (2.17), (2.18) знак перед величиною d обирається той, який забезпечує більшу надійність даного розрахунку основи або фундаменту (тобто збільшує навантаження і зменшує опір матеріалу). Наприклад, обчислюючи активний тиск на огородження (див. §2.7.4) при визначенні розрахункової величини питомої ваги ґрунту за формулою (2.18) приймають знак "плюс", тому що вага ґрунту у даному випадку є навантаженням на огородження і її завищення приводить до збільшення надійності. Навпаки, обчислюючи несучу спроможність ґрунту, яка є функцією його питомої ваги, при визначенні її розрахункової величини за формулою (2.18) приймають знак “мінус”, тому що при цьому знижується несуча спроможність ґрунту, що приводить до підвищення надійності. При визначенні розрахункових значень деформаційних характеристик та міцності завжди приймають знак "мінус“.
Приклад 2.1 Для тугопластичного суглинку одержано 9 визначень питомої ваги g (табл. 2.3).
Виконуємо перевірку на вилучення можливих грубих помилок, для чого обчислюємо
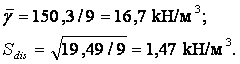
Для n = 9 (табл. 2.1) n = 2,35,
тоді
vSdis = 2,35 × 1,47 = 3,45 кН/м3 .
Таблиця 2.3 - До прикладу 2.1
Номер досліду |
g, kH/м3 |
||
1 |
16,3 |
0,40 |
0,16 |
2 |
15,6 |
1.10 |
1,21 |
3 |
20,3 |
-3,60 |
12,96 |
4 |
16,8 |
-0,10 |
0,01 |
5 |
17,0 |
-0,30 |
0,09 |
6 |
17,1 |
-0,40 |
0,16 |
7 |
15,3 |
1,40 |
1,96 |
8 |
15,0 |
-1,70 |
2,89 |
9 |
16,9 |
-0,20 |
0,04 |
S |
150,3 |
0,00 |
19,49 |
Найбільше відхилення від середнього значення складає 3,60, що більше від 3,45. Таким чином, дослідні дані містять грубу помилку (дослід №3), яка підлягає вилученню.
Заново обчислюємо середнє значення питомої ваги, але вже для восьми дослідів, та суму квадратів відхилень від середнього значення.
Вони складають відповідно 16,25 кН/м3 та 4,903. Після вилучення грубої помилки за нормативне значення питомої ваги приймають її середнє арифметичне. Отже, gn = 16,25 kH/м3.
Для визначення розрахункової величини g обчислюємо середнє квадратичне відхилення та коефіцієнт варіації:
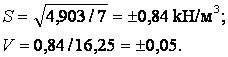
Для оцінки несучої спроможності основ (І група граничних станів) питома вага g визначається з довірчою ймовірністю 0,95.
При a = 0,95 і n - 1 = 7 знаходимо (табл.2.2) ta = 1,90.
Тоді за формулою (2.14)
![]()
Далі скористаємось формулою (2.18): gп = 16,25(1 – 0,034) = 15,7 kH/м3.
Тут значення d прийнято із знаком „мінус”, оскільки у цьому випадку забезпечується більша надійність розрахунку за несучою спроможністю.
При розрахунку за деформаціями (II група граничних станів) маємо при a =0,85 і n-1 =7 ta = 1,12. Отже,
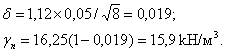
Тут значення d взяте із знаком „мінус” з тих же міркувань, що і в першому випадку.
Приклад 2.2 Для інженерно-геологічного елемента, складеного пластичними супісками, було виконано 27 лабораторних визначень опору зсуву (зрізу) t у трьох серіях (по 9 дослідів у кожній) при значеннях нормального тиску s =100, 200 та 300 кПа (табл.2.4). Раніш ніж приступити до обчислення нормативних та розрахункових значень c і j, виконуємо перевірку на виключення грубих помилок у визначеннях ti при кожному значенні нормального тиску. Необхідні для цього підрахунки наведені в таблиці 2.4. Значення статистичного критерію прийнято n = 2,35 (табл.2.1). У результаті перевірки виявляємо, що при усіх значеннях нормального тиску:
|t - tі | < nSdis,
отже, грубих помилок немає.
Обчислення нормативних та розрахункових значень c і j виконуємо в табличній формі (табл.2.5), куди в графи 2 і 3 заносимо експериментальні дані значень sі та tі. Після обчислень, записаних у графи 4 і 5, визначаємо tgjn та cn. Значення в графі 6 одержуємо після підстановки знайдених tg jn та cn в формулу:
![]()
Таблиця 2.4 - До прикладу 2.2
№ досліду у серії |
s = 100 кПа |
s = 200 кПа |
s = 300 кПа |
||||||
ti, кПа |
ti, кПа |
ti, кПа |
|||||||
1 |
55 |
14,3 |
204,5 |
102 |
19,2 |
368,6 |
150 |
21,4 |
458,0 |
2 |
62 |
7,3 |
53,2 |
138 |
-16,8 |
282,2 |
145 |
26,4 |
697,0 |
3 |
72 |
-2,7 |
7,3 |
126 |
-4,8 |
23,0 |
180 |
-8,6 |
74,0 |
4 |
76 |
-6,7 |
44,9 |
125 |
-3,8 |
14,4 |
198 |
-26,6 |
707,6 |
5 |
70 |
-0,7 |
0,6 |
124 |
-2,8 |
7,8 |
182 |
-10,6 |
112,4 |
6 |
70 |
-0,7 |
0,5 |
122 |
-0,8 |
0,6 |
175 |
-3,6 |
13,0 |
7 |
72 |
-2,7 |
7,3 |
120 |
1,2 |
1,4 |
178 |
-6,4 |
41,0 |
8 |
75 |
-5,7 |
32,5 |
118 |
3,2 |
10,2 |
175 |
-3,6 |
13,0 |
9 |
72 |
-2,7 |
7.3 |
116 |
5,2 |
27,0 |
160 |
+11,4 |
130 |
S |
624 |
-0,3 |
358,0 |
1091 |
-0,2 |
735,2 |
1543 |
-0,4 |
2246 |
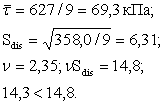 |
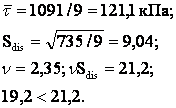 |
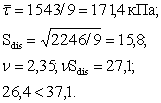 |
|||||||
Використовуючи формули (2.5 - 2.8), обчислюємо tgjn та cn

Таблиця 2.5 - До прикладу 2.2
№ досліду |
si, кПа |
ti, кПа |
s2i 10-3 |
siti10-2 |
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
100 |
55 |
10 |
55 |
70 |
15 |
225 |
2 |
100 |
62 |
10 |
62 |
70 |
8 |
64 |
3 |
100 |
72 |
10 |
72 |
70 |
-2 |
4 |
4 |
100 |
76 |
10 |
76 |
70 |
-6 |
36 |
5 |
100 |
70 |
10 |
70 |
70 |
0 |
0 |
6 |
100 |
70 |
10 |
70 |
70 |
0 |
0 |
7 |
100 |
72 |
10 |
72 |
70 |
-2 |
4 |
8 |
100 |
75 |
10 |
75 |
70 |
-5 |
25 |
9 |
100 |
72 |
10 |
72 |
70 |
-2 |
4 |
10 |
200 |
102 |
40 |
204 |
121 |
19 |
361 |
11 |
200 |
138 |
40 |
276 |
121 |
-17 |
289 |
12 |
200 |
126 |
40 |
252 |
121 |
-5 |
25 |
13 |
200 |
125 |
40 |
250 |
121 |
-4 |
16 |
14 |
200 |
124 |
40 |
248 |
121 |
-3 |
9 |
15 |
200 |
122 |
40 |
244 |
121 |
-1 |
1 |
16 |
200 |
120 |
40 |
240 |
121 |
1 |
1 |
17 |
200 |
118 |
40 |
236 |
121 |
3 |
9 |
18 |
200 |
116 |
40 |
232 |
121 |
5 |
25 |
19 |
300 |
150 |
90 |
450 |
172 |
22 |
484 |
20 |
300 |
145 |
90 |
435 |
172 |
27 |
729 |
21 |
300 |
180 |
90 |
540 |
172 |
-8 |
64 |
22 |
300 |
198 |
90 |
594 |
172 |
-26 |
676 |
23 |
300 |
182 |
90 |
546 |
172 |
-10 |
100 |
24 |
300 |
175 |
90 |
525 |
172 |
-3 |
9 |
25 |
300 |
178 |
90 |
534 |
172 |
-6 |
36 |
26 |
300 |
175 |
90 |
525 |
172 |
-3 |
9 |
27 |
300 |
160 |
90 |
480 |
172 |
12 |
144 |
S |
5400 |
3258 |
126×104 |
7435×102 |
- |
- |
3349 |
Таким чином, у нашому прикладі конкретне граничне рівняння складає:
![]()
на основі якого заповнюємо графу 6.
Після заповнення граф 7 і 8 знаходимо
![]()
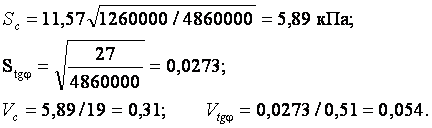
Визначаємо розрахункові значення с і j для розрахунку основ за першою групою граничних станів. Для a = 0,95 та n - 2 = 25 ta = 1,71.
Тоді
dc = 1,71×0,31 = 0,53;
dtgj = 1,71×0,054 = 0,092;
c1 = 19(1 - 0,53) =9 кПа;
tg j1 = 0,51(1 – 0,092) = 0,463; j1 = 25°.
При розрахунках за другою групою граничних станів для a = 0,85 та n-2 = 25 ta =1,055.
Тоді
dc = 1,055×0,31 = 0,33;
dtgj = 1,055×0,054 = 0,057;
cn = 19(1 – 0,033) = 13 кПа;
tg jn = 0,51(1 – 0,057) = 0,481; jn = 26°.
2.2.2 Алгоритм і програма статистичної обробки дослідних даних з визначення характеристик ґрунту
Нормами [6] передбачено, що при визначенні нормативних і розрахункових значень характеристик ґрунту, значення коефіцієнта γg в формулі (2.16) для характеристик міцності ґрунтів (питоме зчеплення с, кут внутрішнього тертя j, тимчасовий опір одноосному стиску Rc) i питомої ваги g визначається за методикою, наведеною у § 2.2.1. Для всіх інших характеристик ґрунту допускається приймати gg = 1, тобто їх розрахункові значення дорівнюють нормативним.
Визначення розрахункових значень характеристик j, c, Rc і g, як видно з § 2.2.1, є досить трудомісткою задачею. Тому статистичну обробку дослідних даних за цими характеристиками доцільно виконувати за допомогою ЕОМ. З цією метою на кафедрі ПЦБ ВДТУ складена спеціальна програма для персональних комп'ютерів, яка передбачає визначення нормативних і розрахункових значень параметрів j, c, Rc і g за результатами дослідних визначень.
Кількість дослідів із визначення однієї характеристики в одному ІГЕ повинна бути не менше 6.
Підготовка ввідних даних для введення в ЕОМ
Програмою передбачається обробка за один раз двох вибірок (сукупностей дослідних даних): однієї для визначення j і с (сукупність дослідних значень граничних напружень зсуву tі), а другої для обробки дослідних даних з визначення Rc або g.
Якщо треба виконувати обробку більшої кількості вибірок, необхідно повторювати роботу з програмою.
Для розрахунку потрібні такі ввідні дані:
1) кількість визначень характеристик, причому при обробці даних із визначення t вони групуються за трьома значеннями нормального напруження: s1 =100 кПа; s2 =200 кПа; s3 =300 кПа і кількість визначень t вводиться окремо для кожного значення s;
2) частинні значення характеристики у відповідній кількості;
3) вказівки до прийняття знака "плюс" чи “мінус” у формулі (2.17). Конкретно вказується, чи підвищує надійність зниження розрахункового значення характеристики.
Алгоритм розрахунку
1. Введення ввідних даних.
2. Вилучення грубих помилок із вибірок дослідних даних.
3. Визначення нормативного значення характеристик (окремо для t або Rc чи g).
4. Визначення середньоквадратичного відхилення характеристик і коефіцієнтів варіації.
5. Визначення коефіцієнта ta при довірчій ймовірності a = 0,85 і a = 0,95.
6. Визначення розрахункових значень характеристики для розрахунків за першою й другою групами граничних станів.
7. Виведення на екран монітора результатів розрахунку.
8. Якщо результати задовольняють користувача, то вони виводяться на друкування. Друкуються такі величини: кількість дослідів після вилучення грубих помилок, нормативне значення характеристики, коефіцієнт варіації, розрахункові значення характеристики для другої й першої групи граничних станів. Результатам розрахунків передує друк ввідних даних.
Нижче наведені результати розрахунків для прикладів 2.1, та 2.2.
СТАТИСТИЧНА ОБРОБКА ХАРАКТЕРИСТИК ГРУНТУ
ПРІЗВИЩЕ: ГРУПА:
ВИХІДНІ ДАНІ
РЕЗУЛЬТАТИ ВИЗНАЧЕННЯ ОПОРУ ЗРІЗУ
|
НОМЕР ДОСЛІДУ |
ПРИ НОРМАЛЬНОМУ НАПРУЖЕННІ |
||
100 кПа |
200 кПа |
300 кПа |
|
1 |
55 |
102 |
150 |
2 |
62 |
138 |
145 |
3 |
72 |
126 |
180 |
4 |
76 |
125 |
198 |
5 |
70 |
124 |
182 |
6 |
70 |
122 |
175 |
7 |
72 |
120 |
178 |
8 |
75 |
118 |
175 |
9 |
72 |
116 |
160 |
КІЛЬКІСТЬ ДОСЛІДІВ ПО ВИЗНАЧЕННЮ ХАРАКТЕРИСТИК 9
ПРИВАТНІ ЗНАЧЕННЯ ХАРАКТЕРИСТИКИ
16,3 15,6 20,3 16,8 17,0 17,1 15,3 15,0 16,9
РЕЗУЛЬТАТИ РОЗРАХУНКУ
| КІЛЬКІСТЬ ДОСЛІДІВ ПО ВИЗНАЧЕННЮ ОПОРУ ЗРІЗУ ПІСЛЯ ВИКЛЮЧЕННЯ ГРУБИХ ПОМИЛОК |
27 |
|---|---|
НОРМАТИВНЕ ЗНАЧЕННЯ ПИТОМОГО ЗЧЕПЛЕННЯ, кПа = |
18,6 |
НОРМАТИВНЕ ЗНАЧЕННЯ КУТА ВНУТРІШНЬОГО ТЕРТЯ, ГРАД = |
27,02 |
КОЕФІЦІЄНТ ВАРІАЦІЇ ПИТОМОГО ЗЧЕПЛЕННЯ = |
0.317 |
КОЕФІЦІЄНТ ВАРІАЦІЇ ТАНГЕНСА КУТА ВНУТРІШНЬОГО ТЕРТЯ = |
0,054 |
РОЗРАХУНКОВЕ ЗНАЧЕННЯ ПИТОМОГО ЗЧЕПЛЕННЯ, кПа |
|
ДЛЯ ДРУГОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
12.4 |
ДЛЯ ПЕРШОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
8,5 |
РОЗРАХУНКОВЕ ЗНАЧЕННЯ КУТА ВНУТРІШНЬОГО ТЕРТЯ, ГРАД |
|
ДЛЯ ДРУГОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
25,7 |
ДЛЯ ПЕРШОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
24,8 |
КІЛЬКІСТЬ ДОСЛІДІВ ПО ВИЗНАЧЕННЮ ХАРАКТЕРИСТИКИ |
|
ҐРУНТУ ПІСЛЯ ВИЛУЧЕННЯ ГРУБИХ ПОМИЛОК = |
8 |
НОРМАТИВНЕ ЗНАЧЕННЯ ХАРАКТЕРИСТИКИ = |
16,3 |
КОЕФІЦІЄНТ ВАРІАЦІЇ = |
0,052 |
РОЗРАХУНКОВЕ ЗНАЧЕННЯ ХАРАКТЕРИСТИКИ: |
|
ДЛЯ ДРУГОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
15,9 |
ДЛЯ ПЕРШОЇ ГРУПИ ГРАНИЧНИХ СТАНІВ = |
15,7 |