1.1.1 Диференціальні рівняння як математичні моделі безперервних детермінованих ЛДС ЗП у часовому просторі

Ще з шкільного курсу фізики нам відомо, що напруга U(t), яка прикладається до котушки з індуктивністю L та внутрішнім опором r (рис. 1.1), урівноважується сумою падіння напруги r·I(t), обумовленго протіканням струму I(t) по внутрішньому опору r, та електрорушійною силою самоіндукції 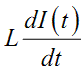, тобто має місце рівність

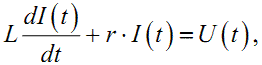(1.1)

яка являє собою диференціальне рівняння 1-го порядку, оскільки одна із змінних, які воно зв'язує між собою, входить в нього разом зі своєю похідною.

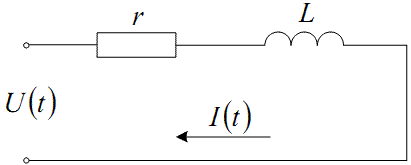
Рисунок 1.1 — Електрична схема підключення котушки індуктивності під напругу

Якщо котушку індуктивності розглядати як динамічну систему (ДС), на вхід якої надходить сигнал U(t), котрий викликає у ній реакцію у вигляді I(t) (рис. 1.2), то диференціальне рівняння (1.1) буде відігравати роль мате- матичної моделі цієї системи, оскільки його розв'язок I(t) = f(U,t) однозначно віддзеркалюватиме процес зміни в часі її реакції на даний вхідний сигнал.

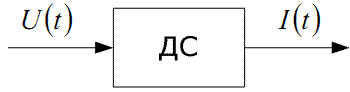
Рисунок 1.2 — Структурна схема котушки індуктивності як динамічної системи

А тепер подамо ту ж саму напругу U(t) на послідовне з'єднання тієї ж самої котушки індуктивності з конденсатором ємністю C (рис. 1.3), напруга на якому, як відомо з курсу фізики, дорівнює

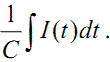
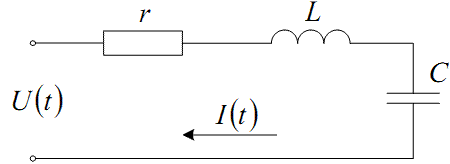
Рисунок 1.3 — Електрична схема підключення під напругу послідовного з'єднання котушки індуктивності та конденсатора

У цьому випадку прикладена до послідовного з'єднання котушки інду- ктивності та конденсатора напруга буде врівноважуватись сумою падіння на- пруги, обумовленого протіканням струму по внутрішньому опору котушки, електрорушійної сили самоіндукції котушки і напруги на конденсаторі, тобто матиме місце рівність

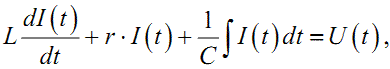(1.2)

яка являє собою інтегро-диференціальне рівняння, оскільки одна із змінних, які воно зв'язує, входить в нього не лише зі своєю похідною, а й зі своїм інтегралом.

Для того, щоб рівняння (1.2) перетворити в чисто диференціальне, про- диференціюємо обидві його частини. В результаті цього диференціювання з урахуванням того, що похідна від невизначеного інтеграла дорівнює підінтегральній функції, отримаємо рівність

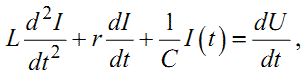(1.3)

яка являє собою диференціальне рівняння 2-го порядку, оскільки одна із змінних, які воно зв'язує, входить в нього не лише зі своєю першою, а й зі своєю другою похідною, що має найвищий порядок у цьому рівнянні, а тому і визначає порядок рівняння.

На підставі міркувань, аналогічних наведеним вище, під час розгляду котушки індуктивності як динамічної системи, в разі розгляду послідовного з'єднання котушки індуктивності та конденсатора як динамічної системи з вхідним сигналом I(t) та реакцією на нього I(t) (рис. 1.2), можна стверджувати, що диференціальне рівняння (1.3) відіграє роль математичної моделі цієї динамічної системи.

Звертаємо увагу на те, що коли система мала у своїй структурі лише один елемент (котушку індуктивності), здатний запасати на якийсь час енергію (індуктивну), то для моделювання процесу зміни станів у ній достатньо було диференціального рівняння 1-го порядку, а коли у структурі системи з'явився ще й другий елемент (конденсатор), здатний запасати на якийсь час енергію (ємнісну), то для моделювання зміни станів у ній уже знадобилось диференціальне рівняння 2-го порядку.

Легко показати, користуючись лише знаннями розділу «Механіка» шкільного курсу фізики, що аналогічна ситуація матиме місце і в динамічних системах з двома елементами, здатними запасати на якийсь час кінетичну та потенціальну енергію.

А у зв'язку з тим, що структура довільної ЛДС ЗП з вхідним сигналом x(t) і реакцією на нього y(t) може мати n елементів, здатних запасати на якийсь час якийсь вид енергії, то адекватно моделювати зміни станів у ні можна лише за допомогою диференціального рівняння n-го порядку

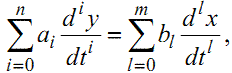(1.4)

для якого виконується умова

(1.5)

що обумовлена здатністю системи фізично реалізуватись під таку модель.

Для отримання розв'язку диференціального рівняння 1-го порядку (1.1) це рівняння необхідно один раз проінтегрувати. В результаті цього інтегрування в розв'язку з'явиться стала інтегрування, для конкретизації якої необхідно задати початкову умову для вихідної координати I(t), тобто задати умову

(1.6)

Це означає, що з множини траєкторій руху, які задаються загальним розв'язком диференціального рівняння 1-го порядку, потрібно вибрати ту, яка в початковий момент часу (

t

I

З фізичної точки зору це означає, що, моделюючи процес зміни струму I(t) в котушці індуктивності після подачі на її затискачі напруги U(t), потрібно врахувати в момент подачі напруги той залишковий струм, який мав місце у цій котушці індуктивності у цей момент в результаті її звільнення від енергії, привнесеної попереднім вхідним сигналом.

Оскільки для отримання розв'язку диференціального рівняння 2-го по- рядку його необхідно проінтегрувати двічі, що викликає появу одна за одною двох сталих інтегрування, то для їх конкретизації уже потрібно знати в початковий момент часу (t = 0)не лише значення вихідної координати I(t), але і значення її першої похідної , тобто початкова умова для рівняння (1.3) на- буває вигляду

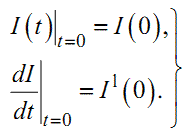(1.7)

Цілком очевидно, що для отримання розв'язку диференціального рів- няння n-го порядку його необхідно проінтегрувати n раз, що викликає появу n сталих інтегрування, для конкретизації яких потрібно знати в початковий момент часу не лише значення вихідної координати y(t), але і значення у цей початковий момент усіх її похідних до (n - 1)порядку включно, тобто початкова умова для рівняння (1.4) має вигляд

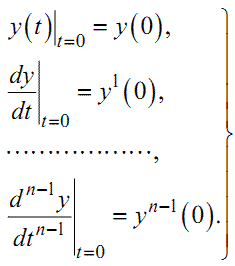(1.8)

Слід відзначити, що для значної кількості ЛДС ЗП характерним є те, що всі елементи їхніх структур, які здатні запасати енергію, після відклю- чення системи цю енергію втрачають, що дає підставу перед новим включен- ням у роботу системи для її моделі у вигляді (1.4) вважати початкові умови нульовими, тобто в системі рівнянь (1.8) вважати усі праві частини такими, що дорівнюють нулю. Це суттєво спрощує подальший процес моделювання.