1.1.2 Перехідна та імпульсна перехідна характеристики безперервних детермінованих ЛДС ЗП

Серед математичних моделей лінійних динамічних систем широке за- стосування знаходять дві їх характеристики в часовій області, які називають перехідною характеристикою h(t) та імпульсною перехідною характеристикою g(t).

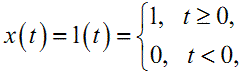(1.9)

маємо

(1.10)

Графічна інтерпретація цього означення показана на рис. 1.4.

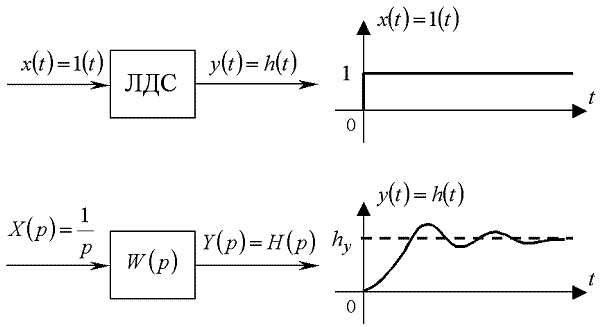
Рисунок 1.4 — Графік реакції h(t) лінійної динамічної системи ЛДС на одиничний стрибок 1(t)

Імпульсна перехідна або вагова характеристика g(t) системи є її реакцією на одиничний імпульсний вхідний сигнал x(t) у вигляді дельтафункції δ(t), для якої справедливо:

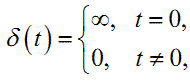(1.11)

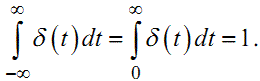(1.12)

Із виразів (1.11), (1.12) випливає, що дельта-функція — це ідеалізація імпульсу одиничної площі з надзвичайно великою висотою і надзвичайно малою протяжністю (рис. 1.5).

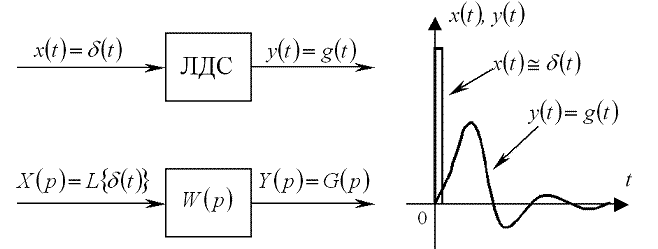
Рисунок 1.5 — Графік реакції g(t) лінійної динамічної системи ЛДС на одиничний імпульс δ(t)

Дуже важливим є те, що сигнал x(t), який діє на вході лінійної динамічної системи з імпульсною перехідною характеристикою g(t) (рис. 1.6), та реакція системи y(t) на цей сигнал пов'язані між собою інтегралом згортки

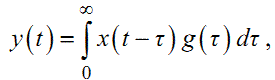(1.13)

який має надзвичайно прозорий зміст — вихідний сигнал динамічної системи формується сумою реакцій на кожний імпульс вхідного сигналу під час по- дання цього вхідного сигналу у вигляді послідовності імпульсів з висотою, що дорівнює значенню вхідного сигналу у відповідний момент часу.

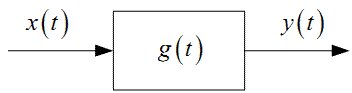
Рисунок 1.6 — Узагальнена структурна схема лінійної динамічної системи