1.2 Математичні моделі безперервних детермінованих ЛДС ЗП на комплексній площині

З курсу операційного числення, що є одним з обов'язкових розділів за- гального курсу вищої математики, який викладається студентам технічних вузів, відомо, що за допомогою оператора Лапласа

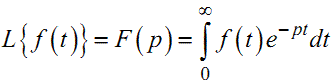(1.14)

кожній функції f часу t , яка задовольняє умову f(t) = 0 при t < 0, умови Діріхле і називається оригіналом, можна поставити у відповідність функцію F комплексної змінної p, яка називається зображенням оригіналу на комплексній площині. Ця відповідність записується у такий спосіб:

(1.15)

Наприклад, часовій функції одиничного стрибка (1.9) на комплексній площині відповідає зображення

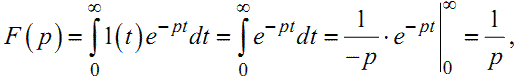(1.16)

або

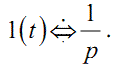(1.17)

Ще один приклад — експоненті e^-αt при t≥0 на комплексній площині відповідає зображення

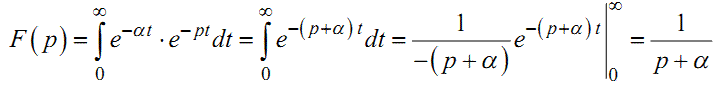(1.18)

або

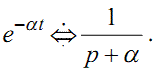(1.19)

Головною перевагою аналізу в області зображень F(p), тобто на комплексній площині, у порівнянні з аналізом в області оригіналів f(t), тобто у часовому просторі, є те, що за нульових початкових умов операції диференціювання оригіналу f(t) у часовому просторі відповідає операція перемноження на комплексну змінну p його зображення F(p) на комплексній площині, тобто

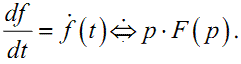(1.20)

Як наслідок цієї властивості маємо:

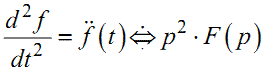(1.21)

та

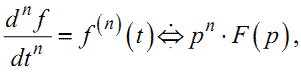(1.22)

а також

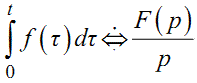(1.23)

та

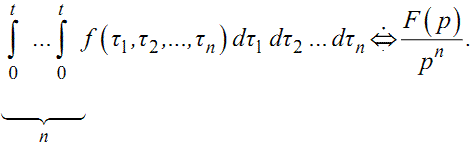(1.24)

Завдяки властивості (1.20) та її наслідкам (1.21) — (1.24) диференціа- льним та інтегральним рівнянням, записаним у часовому просторі, відпові- дають алгебраїчні рівняння на комплексній площині, розв'язувати які набагато простіше, оскільки цьому вчать ще у школі.

Наприклад, диференціальному рівнянню в області оригіналів x(t), y(t)

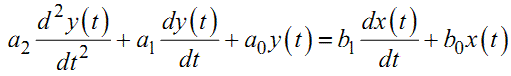(1.25)

на комплексній площині відповідає алгебраїчне рівняння

(1.26)

відносно зображень X(p) та Y(p). Його розв'язком є функція Y(p), яку із рівняння (1.26) можна визначити у такий спосіб:

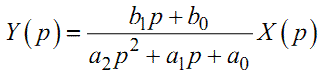(1.27)

або

(1.28)

де

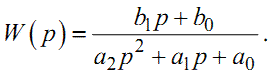(1.29)

Якщо X(p) вважати зображенням сигналу x(t), який надходить на вхід динамічної системи (рис. 1.7), математичну модель якої можна записати у вигляді (1.28), де y(t) є реакцією цієї системи на вхідний сигнал x(t), то функцію W(p) можна інтерпретувати як передаточну (або передатну) функцію системи.

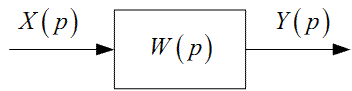
Рисунок 1.7 — Узагальнена структурна схема динамічної системи в області зображень

Як видно із виразів (1.27) — (1.29), передаточна функція W(p) не залежить від зовнішніх сигналів, які діють на систему, та однозначно характеризує внутрішню структуру і властивості лише самої системи.

А тому ця функція є однією із найважливіших математичних моделей лінійних систем, для яких перетворення Лапласа (1.14) задає взаємно одно- значну відповідність між оригіналами та їх зображеннями.

Із виразу(1.28) випливає, що, знаючи зображення X(p) вхідного сигналу x(t) та зображення Y(p) реакції системи y(t) на цей сигнал, передаточну функцію можна отримати, взявши їх відношення, тобто

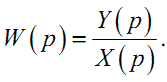(1.30)

Варто нагадати, що обернене перетворення Лапласа

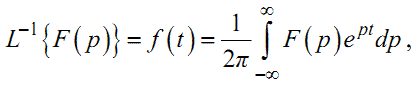(1.31)

згідно з яким за відомим зображенням F(p) можна знайти оригінал f(t) , як правило, використовується лише для побудови таблиць відповідності між f(t) та F(p), а в практиці аналізу частіше використовуються формули розкладання, одна з яких — для некратних полюсів p_iзображення

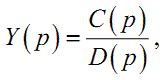(1.32)

де C(p), D(p) — багаточлени за степенями p порядків m та n , відповідно, — має вигляд

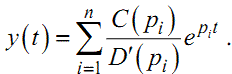(1.33)

Нагадаємо, що p_i — це корені рівняння

(1.34)

а

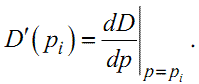(1.35)

Наведемо приклад використання формули розкладання (1.33).

Нехай маємо зображення невідомого нам оригіналу у вигляді

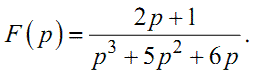(1.36)

Треба визначити його оригінал f(t).

Очевидно, що для нашого прикладу:

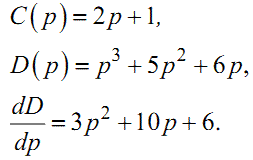(1.37)

Знайдемо полюси зображення (1.36), тобто корені рівняння

(1.38)

Привівши рівняння (1.38) до вигляду

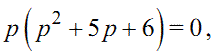(1.39)

легко бачити, що полюсами зображення (1.36) є:

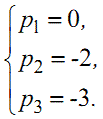(1.40)

Підставляючи (1.37) та (1.40) у формулу розкладання (1.33), отримає- мо:

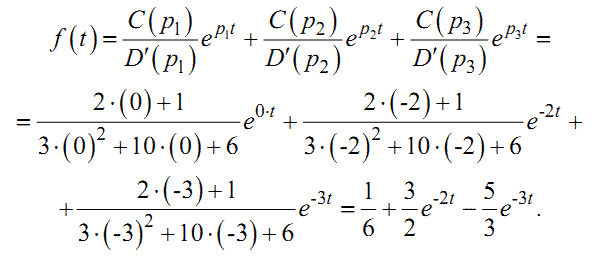
Функція

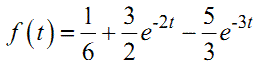(1.41)

і є оригіналом зображення виразу (1.36). Ще раз нагадуємо, що оригінал визначається лише при значеннях t≥0.

Зв'яжемо передаточну функцію W(p) ЛДС ЗП з її перехідною h(t) та імпульсною перехідною g(t) характеристиками.

Оскільки згідно зі співвідношенням (1.28) зображення за Лапласом ви- хідного сигналу Y(p) лінійної динамічної системи є добутком передаточної функції цієї системи W(p) та зображення за Лапласом вхідного сигналу системи X(p), яке в разі виконання (1.9), згідно з (1.17), дорівнюватиме , то для зображення за Лапласом перехідної характеристики

H(p)

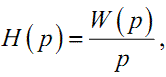(1.42)

що, в свою чергу, дає нам право записати

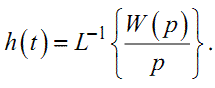(1.43)

Легко бачити, що зображення за Лапласом дельта-функції дорівнює

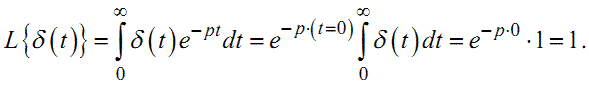(1.44)

Тож, якщо при

(1.45)

за визначенням

(1.46)

то із (1.28) випливає, що

(1.47)

Тобто передаточна функція лінійної динамічної системи є зображенням за Лапласом її імпульсної перехідної характеристики, і навпаки

(1.48)

Із співвідношень (1.42) і (1.47) випливає, що

(1.49)

А це, в свою чергу, означає, що в області оригіналів справедливим є рівняння

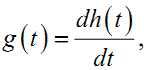(1.50)

тобто, що імпульсну перехідну характеристику

g(t)

Підводячи підсумок викладеному вище, можна стверджувати, що ма- тематичну модель ЛДС ЗП у вигляді передаточної функції W(p) можна визначити, поділивши перетворену за Лапласом реакцію системи y(t) на перетворений за Лапласом вхідний сигнал x(t) . Цілком очевидно, що до перетворення за Лапласом і експериментально зафіксований вхідний сигнал x(t), і експериментально зафіксовану реакцію y(t) системи на цей сигнал потрібно апроксимувати відповідними функціями аргументу t. Згідно з теоремою Вейєрштрасса майже завжди це можна зробити за допомогою поліномів за степенями аргументу t, перетворення за Лапласом яких приводить до відношення поліномів за степенями аргументу p. Очевидним є також і те, що найбільш просто задача ідентифікації такої системи за цим алгоритмом буде розв'язуватись, якщо вхідним сигналом динамічної системи є одиничний стрибок 1(t) або одиничний імпульс δ(t), з перетворених за Лапласом реакцій системи на кожен із яких одразу отримуємо передаточну функцію згідно зі співвідношеннями (1.42) або (1.47).

На завершення цього підрозділу покажемо, як, отримавши передаточну функцію W(p) ЛДС ЗП, побудувати математичну модель цієї системи у вигляді диференціального рівняння.

Нехай математична модель ЛДС ЗП на комплексній площині має ви- гляд

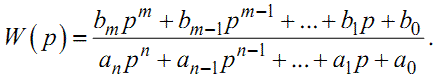(1.51)

Підставивши значення

W(p)

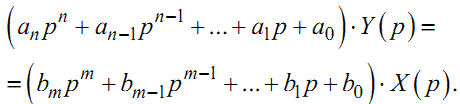(1.52)

Розкриваючи дужки в рівності (1.52) і враховуючи те, що перемножен- ню зображення на p відповідає диференціювання оригіналу за t, приходимо до диференціального рівняння (1.4).