1.3 Математичні моделі безперервних детермінованих ЛДС ЗП в частотній області

Як показано у попередньому підрозділі, достатньо повну інформацію про динаміку лінійної системи несе її передаточна функція, яка є функцією комплексної змінної p = σ + jω.

Якщо накласти умову

(1.53)

то передаточна функція W(p) вироджується у функцію уявної частини jω комплексної змінної p, тобто в W(jω).

До прикладу, нехай

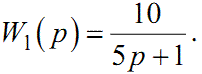(1.54)

За виконання умови (1.43) із (1.44) маємо:

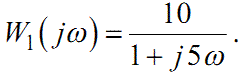(1.55)

Функцію W₁(jω) шляхом очевидних перетворень можна привести до такої форми

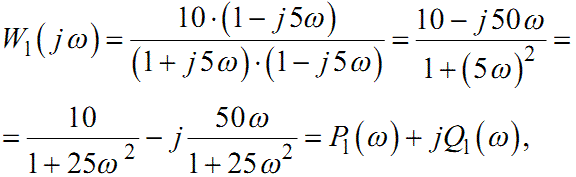(1.56)

де

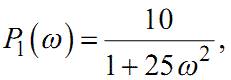(1.57)

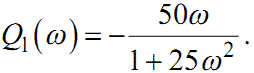(1.58)

Вирази (1.55) — (1.58) за своєю структурою справедливі для довільної функції W(p). Оскільки як функція W(jω), так і її складові P(ω) та Q(ω) у своїй структурі містять всі коефіцієнти передаточної функції W(p) , то можна стверджувати, що кожна з них несе однакову кількість інформації про динаміку системи, яка характеризується цією передаточною функцією. У цьому легко переконатись на наведеному прикладі.

З теорії комплексних чисел відомо, що при ω = ω^*комплексне число

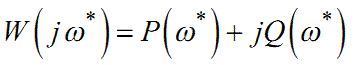(1.59)

можна записати не тільки в алгебраїчній формі (1.49), а й у показниковій:

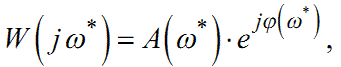(1.60)

де

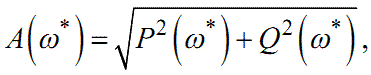(1.61)

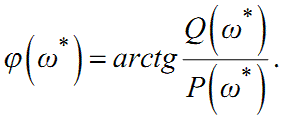(1.62)

Оскільки параметр  в усіх наведених вище виразах має чітко визна- чений фізичний сенс — це кругова частота, то всі функції, що залежать від нього, називаються частотними характеристиками, з яких:

P(ω) — дійсна частотна характеристика,

Q(ω) — уявна частотна характеристика,

A(ω) — амплітудна частотна характеристика,

φ(ω) — фазова частотна характеристика,

W(jω) — амплітудно-фазова частотна характеристика.

Для співвідношень (1.59) — (1.62), які пов'язують між собою частотні характеристики, слід додати ще два, які є очевидними для всіх, хто знайомий з теорією комплексних чисел, а саме:

(1.63)

(1.64)

Амплітудну та фазову частотні характеристики A(ω) та φ(ω) динамічної системи легко отримати експериментально за допомогою спеціального комплексу, який випускається серійно і містить у собі генератор синусоїдальних коливань змінної частоти, подвійний піковий вольтметр, фазометрчастотомір та пристрій для перетворення фізичних параметрів процесів на вході та виході системи в електричний сигнал і для їх узгодження. Зазначимо, що амплітудно-фазову частотну характеристику з експерименту можна побудувати тільки для стійких об'єктів.

Експеримент з отримання частотних характеристик A(ω) та φ(ω) полягає в тому, що на вхід системи від генератора синусоїдальних коливань подаємо сигнал

(1.65)

з фіксованими частотою ω₁ = 2πf₁, де f₁ — реальна частота у герцах, та амплітудою X₁(ω₁).

Після закінчення перехідного процесу, тривалість якого визначається чотирма еквівалентними сталими часу цієї системи, на її виході встановляться коливання

(1.66)

Замірявши подвійним піковим вольтметром одночасно значення амплітуди X₁(ω₁) сигналу на вході системи та Y₁(ω₁) на її виході та взявши їх відношення, отримаємо значення амплітудної частотної характеристики системи на частоті ω₁, тобто

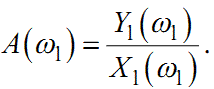(1.67)

За допомогою фазометра-частотоміра на цій ж частоті ω₁ заміряємо зсув фаз φ(ω₁), який виникає між сигналами x₁(t) та y₁(t) — він безпосередньо задає значення фазової частотної характеристики φ(ω₁) на частоті ω₁.

Дискретно змінюючи частоту вхідного сигналу від нуля до значень ω_n, за яких можна вважати, що

(1.68)

і здійснюючи дії, що описані вище, отримаємо скінченну множину чисел

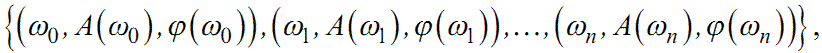(1.69)

яка дискретно задає амплітудну та фазову частотні характеристики A(ω) і φ(ω) системи.

Для отримання неперервних функцій A(ω) та φ(ω) залишається тільки здійснити апроксимацію послідовностей чисел

(1.70)

(1.71)

за допомогою відомих інтерполяційних процедур, або використавши спеціально підібрані формули для A(ω) і φ(ω) та суму квадратів відхилень як критерій оптимізації процедури.

У разі використання першого шляху для отримання W(jω) необхідно підставити інтерполяційні вирази для A(ω) і φ(ω) у формулу (1.60), а потім за допомогою іншої стандартної процедури перейти від W(jω) до W(p).

Другий шлях дозволяє одразу отримати формулу для W(p).

Алгоритм побудови W(p) за цим підходом такий: спочатку висуваємо гіпотезу про те, що динаміка системи, яка розглядається, описується передаточною функцією

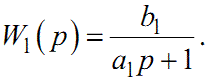(1.72)

Із формули (1.72) видно, що для ідентифікації системи необхідно знайти лише два коефіцієнти a₁ та b₁

Використовуючи формули (1.59) — (1.62) та (1.72), знаходимо, що

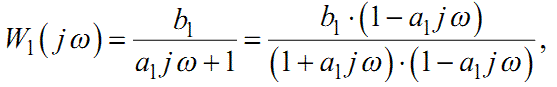(1.73)

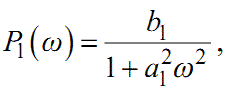(1.74)

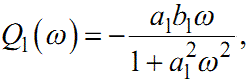(1.75)

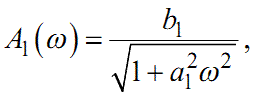(1.76)

(1.77)

Підставляючи у формулу (1.76) значення ω₀, A(ω₀); ω₁, A(ω₁) чи якісь інші дві пари із (1.70), складаємо систему двох рівнянь з двома невідомими a₁, b₁. Розв'язавши цю систему чисельними методами на ПЕОМ, отримаємо оцінки коефіцієнтів a1, b₁.

А використовуючи значення ω₀, φ(ω₀); ω₁ φ(ω₁) ... ω_n,φ(ω_n) із (1.71) та значення коефіцієнта a₁, знайденого на попередньому етапі, вичислимо оцінку

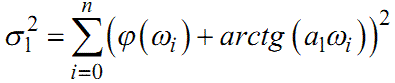(1.78)

суми квадратів відхилень експериментальних значень фазової частотної характеристики від її значень, що визначаються за вибраною моделлю (1.77).

Після цього висуваємо гіпотезу, що динаміка системи описується якоюсь іншою передаточною функцією і для її конкретного виду повторюємо всю описану вище процедуру.

У результаті отримаємо оцінку σ₂²

Якщо

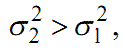(1.79)

то найкращу апроксимацію передаточної функції системи за експеримента- льними даними (1.70), (1.71) забезпечує формула (1.72). Якщо ж

(1.80)

то пошук треба продовжувати.

Дві практичні поради:

1). Якщо умова (1.68) виконується, то це означає, що порядок m полі- нома у чисельнику передаточної функції системи менший за порядок n полінома в її знаменнику.

У цьому легко переконатись, проаналізувавши вираз для A(ω), записаний у загальному вигляді.

Цю умову можна сформулювати ще й так: для реальних інерційних си- стем, для яких

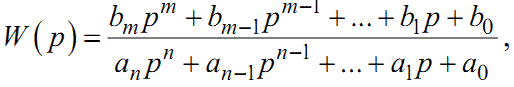(1.81)

завжди виконується умова

(1.82)

2). a). Якщо в (1.71) є таке ω_m, для якого

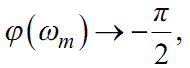(1.83)

то в (1.81) n = 1.

б). Якщо в (1.71) є таке ω_m, для якого

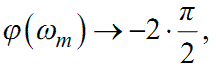(1.84)

то в (1.81) n = 2.

в). Якщо в (1.71) є таке ω_m, для якого

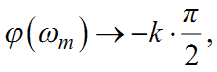(1.85)

то в (1.81) n = k.

Тож, отримавши експериментально значення множини (1.71), одразу можемо визначити порядок n системи і загальний вигляд знаменника її передаточної функції.

А оскільки для реальних систем завжди виконується умова (1.82), то таке попереднє визначення порядку полінома знаменника передаточної функції суттєво скорочує кількість можливих варіантів в задачі синтезу моделі системи за даною процедурою.

А наостанок зауважимо таке.

Ввівши умову (1.53), від перетворення за Лапласом, яке кожній функції, визначеній на часовій осі як оригінал, ставить у відповідність функцію на комплексній площині, переходимо до перетворення Фур'є, яке відображає оригінали на частотну вісь комплексної площини. Саме такий зміст вкладено у назву підрозділу, що випливає із всього викладеного вище.