Нехай відомо, що процеси у динамічній системі описуються диферен- ціальним рівнянням

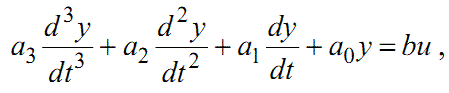(1.86)

де u — сигнал управління, а y — реакція системи на нього.

Позначимо

(1.87)

Тоді

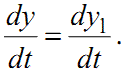(1.88)

Введемо заміну

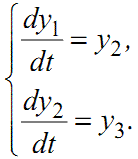(1.89)

Перепишемо рівняння (1.86) у формі:

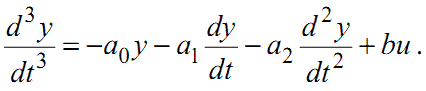(1.90)

З урахуванням (1.87) – (1.89) рівняння (1.90) можна записати у вигляді

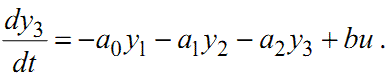
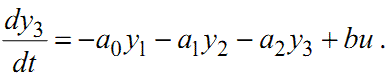(1.91)

У результаті цих перетворень диференціальне рівняння 3-го порядку (1.86) відносно координати y приведено до системи трьох диференціальних рівнянь 1-го порядку відносно координат y₁, y₂, y₃, тобто еквівалентом для (1.86) є система

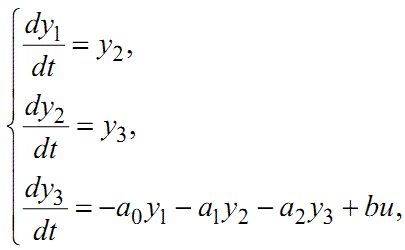(1.92)

яку можна переписати у матричній формі у вигляді

(1.93)

де

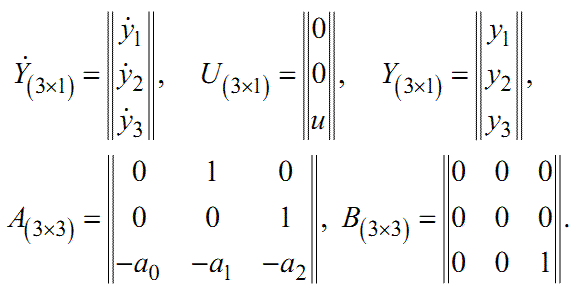(1.94)

Матричне рівняння (1.93) легко узагальнюється на довільний порядок вектора Y, який характеризує стан системи, та вектора управління U за умови лише, що

(1.95)

Вирази (1.92) або (1.93) та (1.94) задають математичну модель динамі- чної системи у просторі змінних її стану, до яких відносять саму вихідну координату y та її (n - 1) похідну.

Запис математичної моделі системи у просторі змінних стану широко використовується в теорії автоматичного управління під час розв'язання задач синтезу оптимального управління.

В літературі до 80-х років при n = 3 простір змінних стану було прийнято називати фазовим простором, а при n = 2 — фазовою площиною.