ІДЕНТИФІКАЦІЯ ДЕТЕРМІНОВАНИХ ЛІНІЙНИХ ДИНАМІЧНИХ
СИСТЕМ З ЗОСЕРЕДЖЕНИМИ ПАРАМЕТРАМИ
2.1 Решітчасті функції та скінченні різниці
Нехай f(t) — неперервна функція, графік якої має вигляд, наведений на рис. 2.1, а.
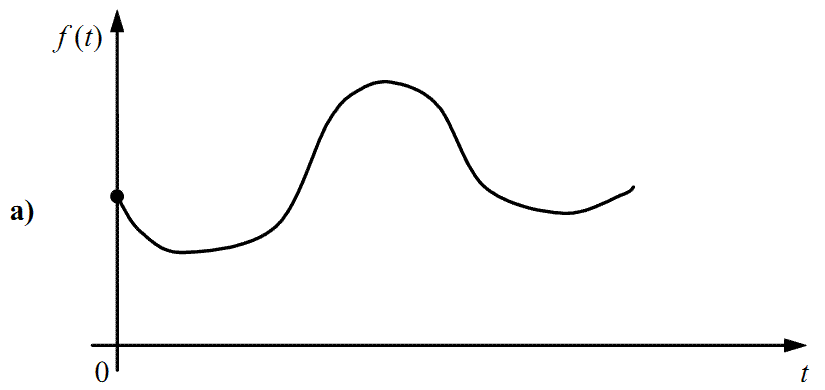
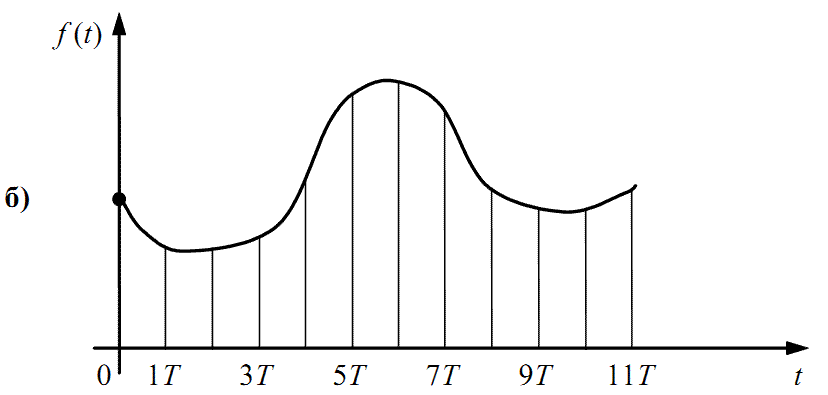
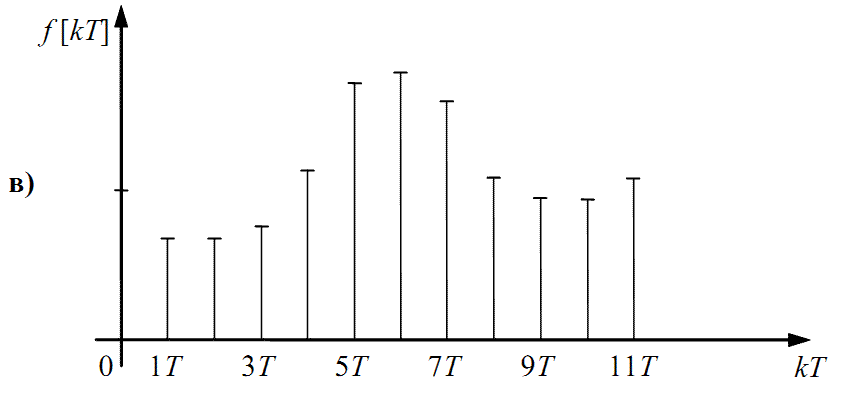 Рисунок 2.1 — Графіки неперервної f(t) і породженої нею
решітчастої f[kT] функцій
Рисунок 2.1 — Графіки неперервної f(t) і породженої нею
решітчастої f[kT] функційВиберемо інтервал дискретності T і визначимо значення функції f(t) лише при значеннях аргументу t, кратних T (рис. 2.1, б).
У результаті цих дій отримаємо функцію f[kT] дискретного аргументу kT (k = 0,1,2,...)(рис. 2.1, в), яку математики домовились називати «решітчастою».
Записується алгоритм породження решітчастої функції f kT із неперервної f(t) у такий спосіб:
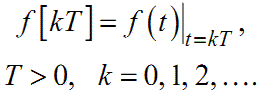 |
(2.1) |
Приклад 1. Нехай
| (2.2) |
| (2.3) |
Згідно з алгоритмом (2.1) решітчаста функція f1[kT], яка породжується функцією (2.2) за умови (2.3), має вигляд:
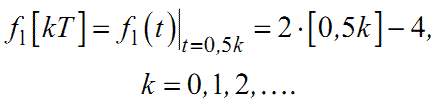 |
(2.4) |
Приклад 2. Нехай
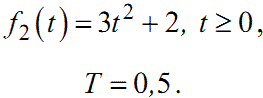 |
(2.5) (2.6) |
Цій неперервній функції відповідає решітчаста, яка визначається у такий спосіб:
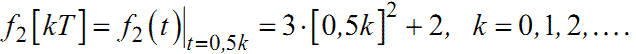 |
(2.7) |
Графіки решітчастих функцій (2.4), (2.7) наведені на рис. 2.2.
Із формул (2.4) та (2.7) легко бачити, що після вибору числового значення інтервалу дискретності T решітчаста функція
f
[kT
] стає функцією лише аргументу k, а тому автори багатьох книг записують її у вигляді не f[kT], а f[k]. Роблячи так, слід пам'ятати, по-перше, що коефіцієнти у функціях f[k] і f[kT] не збігаються, а по-друге, що для відтворення їх породної неперервної функції f(t) необхідно порядковий номер k, який виступає як аргумент решітчастої функції f(k), помножити на числове значення інтервалу дискретності T до виконання операції над ним. Для того, щоб не тримати цього у пам'яті, будемо зберігати період дискретності T в аргументі решітчастої функції f[kT].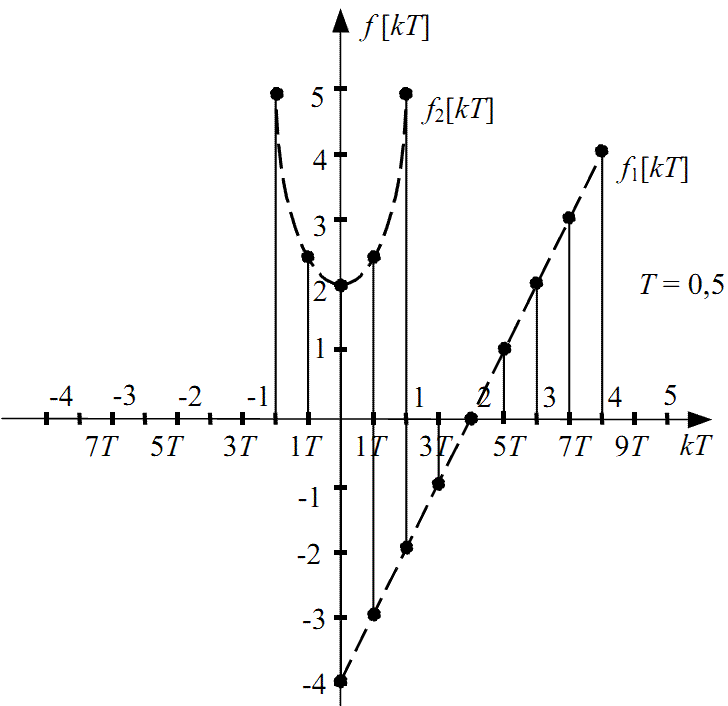
Рисунок 2.2 — Графіки решітчастих функцій f1[kT] = 2[0,5k] - 4 та f2[kT] = 3[0,5]2 + 2 при T = 0,5
Як відомо з курсу математичного аналізу, швидкість зміни неперервної
функції f(t) у кожній точці графіка характеризується значенням її похідної ![]() у цій точці, числове значення якої дорівнює тангенсу кута нахилу до-
тичної до графіка, проведеної через цю ж точку (рис. 2.3).
у цій точці, числове значення якої дорівнює тангенсу кута нахилу до-
тичної до графіка, проведеної через цю ж точку (рис. 2.3).
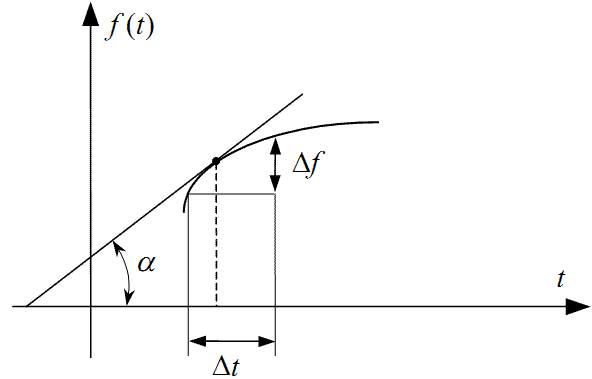 Рисунок 2.3 — Геометрична інтерпретація похідної f(t) від функції f(t)
Рисунок 2.3 — Геометрична інтерпретація похідної f(t) від функції f(t)Відомо, що похідна ![]() є функцією f(t), яка визначається із співвід-
ношення:
є функцією f(t), яка визначається із співвід-
ношення:
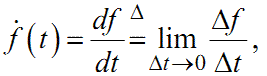 |
(2.8) |
яке не може мати місця для решітчастих функцій.
Але, оскільки сусідні значення аргументу kT решітчастої функції f[kT] відрізняються на T, то, сформувавши різницю
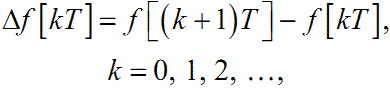 |
(2.9) |
ми можемо формально використати цю різницю Δf[kT] для характеристики швидкості зміни решітчастої функції f[kT] у точці з аргументом kT.
Різницю Δf[kT] називають прямою скінченною різницею першого порядку решітчастої функції f[kT].
За аналогією з (2.9) можна визначити пряму скінченну різницю другого порядку
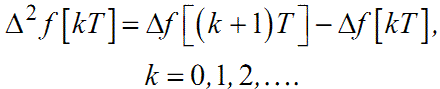 |
(2.10) |
Якщо у вираз (2.10) підставити значення Δf[kT] та Δf[(k+1)T], визначені за формулою (2.9), отримаємо:
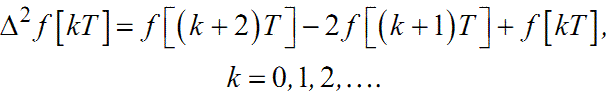 |
(2.11) |
Узагальнюючи (2.9) та (2.10), маємо:
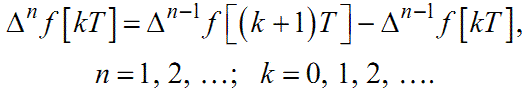 |
(2.12) |
При розкритті формули (2.12) для конкретних n варто пам'ятати, що
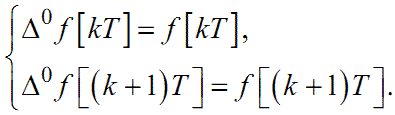 |
(2.13) |
Відомо, що значення похідної f(t) від неперервної функції f(t) у точці з аргументом t не залежить від того зліва чи справа наближається Δt до нуля (див. формулу (2.8)). Інша ситуація виникає при наближенні до точки з аргументом kT під час аналізу решітчастої функції f[kT], а тому для характеристики швидкості її зміни крім прямої скінченної різниці Δf[kT] першого порядку вводять ще й обернену скінченну різницю першого порядку за фор- мулою
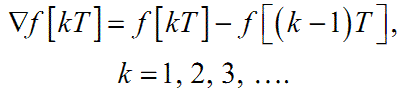 |
(2.14) |
Нагадаємо, що символи «Δ» та «∇» є грецькими літерами, відповідно, «дельта» та «набла».
На рис. 2.4 показано, наскільки суттєво можуть відрізнятись пряма Δf[kT] та обернена ∇f[kT] скінченні різниці першого порядку решітчастої функції f[kT] при значенні аргументу kT = 4T.
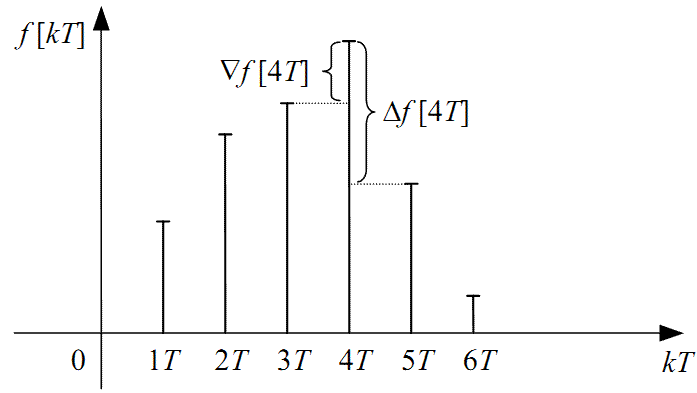
Рисунок 2.4 — Геометрична інтерпретація відмінності між прямою Δf[kT] та оберненою ∇f[kT] скінченними різницями першого порядку у точці з аргументом kT = 4T
За аналогією з (2.12) визначається і обернена скінченна різниця ∇nf[kt] порядку n :
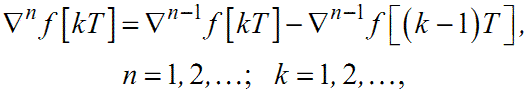 |
(2.15) |
де, як і в (2.13),
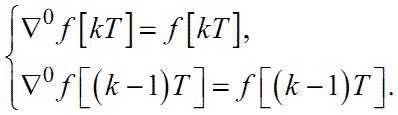 |
(2.16) |
При n = 2 із формули (2.15) отримаємо
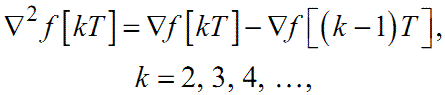 |
(2.17) |
або, з урахуванням (2.14):
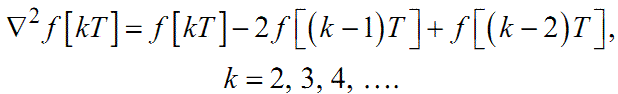 |
(2.18) |
Як приклад знайдемо Δf[kT], Δ2f[kT] та ∇f[kT], ∇2f[kT] для решітчастих функцій f1[kT], f2[kT], визначених формулами (2.4) та (2.7).
Для функції f1[kT]:
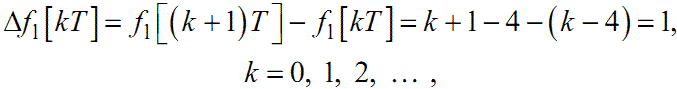 |
(2.19) |
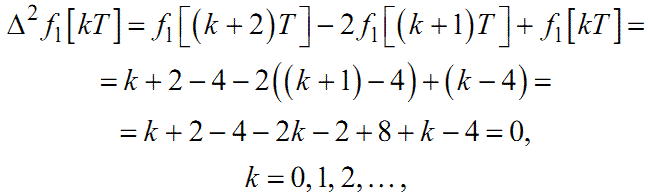 |
(2.20) |
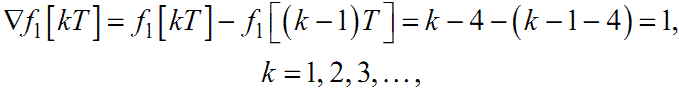 |
(2.21) |
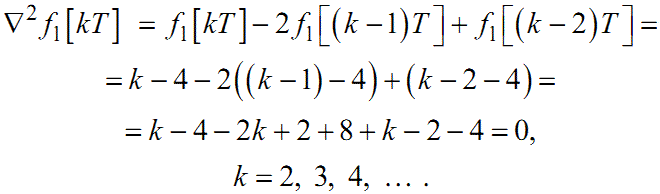 |
(2.22) |
Для функції f2[kT]:
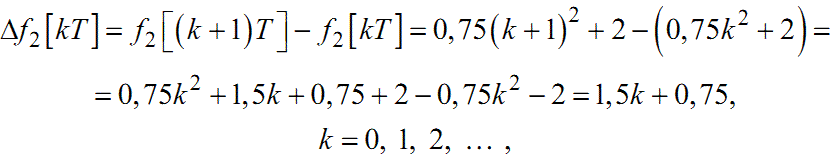 |
(2.23) |
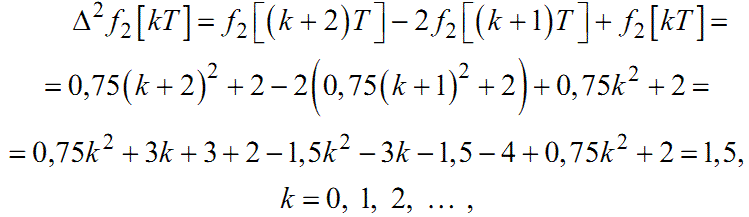 |
(2.24) |
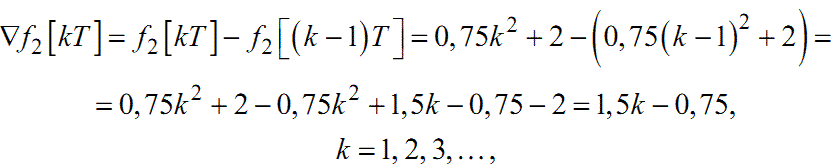 |
(2.25) |
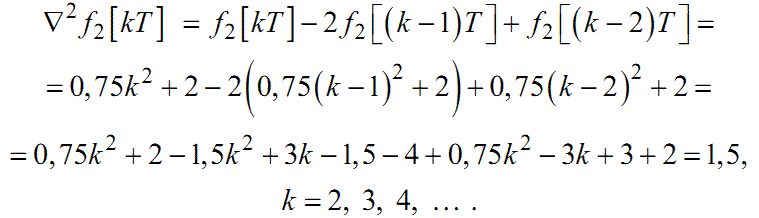 |
(2.26) |
Як видно з отриманих результатів, скінченні різниці першого порядку від лінійної решітчастої функції є константами, а другого порядку дорівнюють нулю. Нагадаємо, що і перша похідна від лінійної неперервної функції є константою, а друга похідна теж дорівнює нулю. Така ж аналогія спостерігається і між решітчастою та неперервною квадратичними функціями.


