ЧАСТИНА І
ІДЕНТИФІКАЦІЯ ДЕТЕРМІНОВАНИХ ЛІНІЙНИХ ДИНАМІЧНИХ
СИСТЕМ З ЗОСЕРЕДЖЕНИМИ ПАРАМЕТРАМИ

2.2 Рівняння в скінченних різницях та різницеві рівняння


В попередньому підрозділі встановлено, що аналогом похідної l-го по-рядку, де l = 1, 2, ..., n, для решітчастої функції f [kT] є пряма Δlf [kT] та обернена ∇lf [kT] скінченні різниці того ж порядку

Очевидним наслідком цієї аналогії є те, що для решітчастих функцій x [kT] та y [kT] можна сконструювати рівняння в скінченних різницях Δlf [kT] (l = 0,1, 2, ..., n), Δqx [kT] (q = 0,1, 2, ..., m) або ∇ly [kT] (l = 0,1, 2, ..., n), ∇qx [kT] (q = 0,1, 2, ..., m), яке буде аналогом диференціального рівняння відносно породних функцій y(t), x(t) та їх похідних y(l)(t) (l = 1, 2, ..., n), x(q) (t) (q = 1, 2, ..., m).

Покажемо на прикладі як можна побудувати дискретний аналог диференціального рівняння.

Нехай маємо диференціальне рівняння

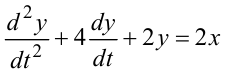  (2.27)

з початковими умовами

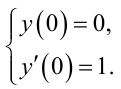  (2.28)

Нехай T — період дискретності функцій x(t), y(t) для породження решітчастих функцій x[kT], y[kT].

Нагадаємо, що аргументи t і kT пов’язані між собою співвідношенням:

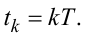  (2.29)

Зрозуміло, що похідній , яку маємо у рівнянні (2.27), в його дискретному аналозі відповідатиме вираз

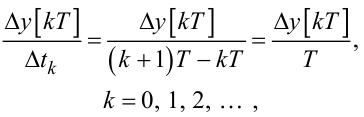  (2.30)

а другій похідній — вираз

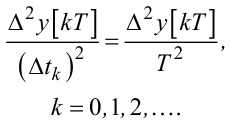  (2.31)

Підставляючи (2.29) — (2.31) у рівняння (2.27), (2.28), отримаємо:

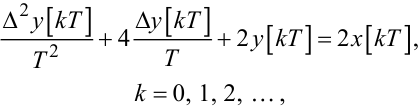  (2.32)
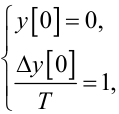  (2.33)

або

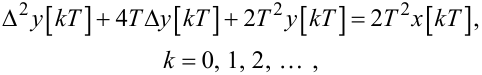  (2.34)
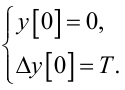  (2.35)

Зрозуміло, що чим меншим буде значення періоду дискретності T, тим менше будуть відрізнятись один від одного значення tk та tk+1 або tk-1 і, як наслідок, ближчими до розв’язку y(t) диференціального рівняння (2.27) у точках tk будуть розв’язки y[kT] рівняння в скінченних різницях (2.34).

Найбільш просто рівняння (2.34) розв’язується шляхом перетворення його в різницеве, яке містить у собі не скінченні різниці, а значення решітча- стих функцій, взятих при декількох значеннях аргументу.

Для здійснення цього перетворення необхідно у рівняннях (2.34), (2.35) замість скінченних різниць Δy[kT], Δ2[kT] підставити їхні значення, взяті з формул (2.9), (2.11).

Здійснивши це, отримаємо:

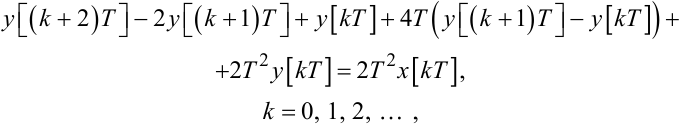  (2.36)
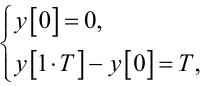  (2.37)

або

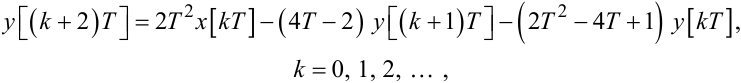  (2.38)
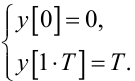  (2.39)
Вибравши конкретне значення T та сформувавши із заданої функції x(t) решітчасту x[kT], шляхом підстановки по черзі k = 0, потім k = 1 і так далі у рівняння (2.38) отримаємо стільки значень розв’язку y[kT], скільки нам треба.

Отримати різницеве рівняння через обернені скінченні різниці ∇y[kT] та ∇2y[kT] пропонуємо самостійно як завдання на закріплення матеріалу. Також пропонуємо перетворити у різницеве довільне диференціальне рів- няння третього порядку із самостійно заданими коефіцієнтами, початковими умовами та правою частиною