2.3 Дискретне перетворення Лапласа та Z-перетворення

У першому розділі було показано, що лінійні диференціальні рівняння можна розв’язувати не лише безпосередньо, але й завдяки попередньому їх перетворенню в алгебраїчні рівняння комплексної змінної із застосуванням прямого та оберненого перетворень Лапласа.

Покажемо, що аналогічну процедуру можна застосувати і до різнице- вих рівнянь

Нехай y[kT] (k = 0, 1, 2, ...) є решітчастою функцією, породженою неперервною функцією-оригіналом y[t] з періодом дискретності T, для якої, як відомо, справедливо:

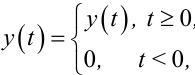(2.40)

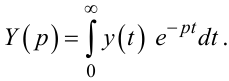(2.41)

Оскільки

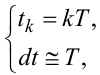(2.42)

то інтеграл у (2.41) можна з деякою похибкою, яка зменшується із зменшен- ням значення T, записати у вигляді суми

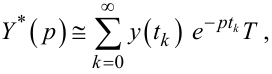(2.43)

або

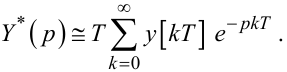(2.44)

Введемо нову комплексну змінну q у такий спосіб

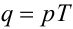(2.45)

і запишемо суму, яка стоїть у правій частини виразу (2.44), у вигляді:

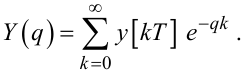(2.46)

Формула (2.46) задає дискретне перетворення Лапласа Y(q) решітчастої функції y[kT].

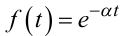(2.47)

є функція

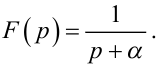(2.48)

Знайдемо дискретне зображення за Лапласом решітчастого аналога

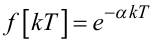(2.49)

цієї експоненти, використавши формулу (2.46)

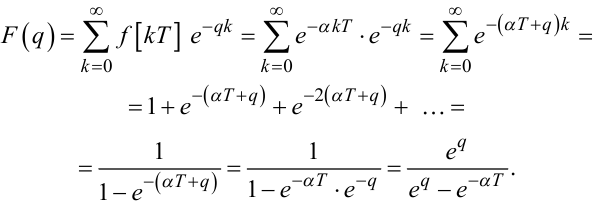(2.50)

Нагадаємо, що у перетвореннях (2.50) використано формулу суми чле- нів нескінченно спадної геометричної прогресії зі знаменником .

Порівнюючи формули (2.48) та (2.50), бачимо, що зображення за Лапласом неперервної експоненти є набагато простішим за своєю структурою, аніж аналогічне зображення її решітчастого аналога. Для більш складних функцій громіздкість зображень за Лапласом їх решітчастих аналогів суттєво наростає.

Ось чому сьогодні дискретне перетворення за Лапласом повністю витіснене з практики аналізу дискретних систем більш простим Z-перетворенням, яке отримується шляхом заміни у формулі (2.46)

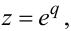(2.51)

тобто

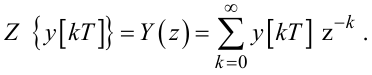(2.52)

Прямою підстановкою (2.51) у (2.50) знайдемо, що Z-перетворення ре- шітчастої експоненти має вигляд:

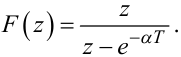(2.53)

Порівнюючи (2.53) з (2.48), бачимо, що вони мають однакову структуру — і у першому, і у другому випадках маємо дробово-раціональні функції, які є відношеннями поліномів у одному випадку за степенями p, а у другому — за степенями z .

Слід пам’ятати, що e^-αT за заданих α і T — це є число, наприклад при α = 1 і T = 2 — це 0,135

Як ще один приклад знайдемо Z-перетворення одиничної решітчастої функції 1[kT], k = 0,1,... .

Оскільки одиничну функцію 1(t) можна отримати з експоненти e^-αT, поклавши α = 0, то одинична решітчаста функція 1[kT] є теж окремим випадком решітчастої експоненти при α = 0. А тому для отримання Z-перетворення 1[kT] достатньо покласти у формулі (2.53) α = 0. Таким чином:

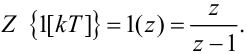(2.54)

У справедливості формули (2.54) легко пересвідчитись і за допомогою основної формули (2.52) Z-перетворення, підставляючи y[kT] = 1[kT] і знаходячи суму членів нескінченно спадної геометричної прогресії із знаменником z^-1.

Оскільки оператор Z-перетворення отримано з перетворення Лапласа шляхом двох лінійних підстановок, всі властивості перетворення Лапласа справедливі і для Z-перетворення, наприклад:

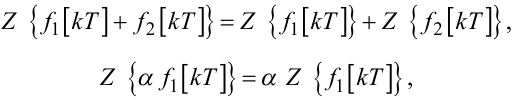(2.55) (2.56)

де α — число, значення якого не залежить від аргументу kT функції f₁[kT].

Під час Z-перетворення різницевих рівнянь доводиться знаходити Z-зображення зсунутих вправо чи вліво значень решітчастих функцій, відносно яких ці рівняння складені, а тому побудуємо алгоритми їх знаходження

Спочатку розглянемо зсув вправо:

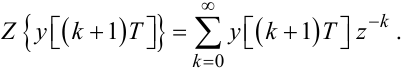(2.57)

Нехай k + 1 = m, тоді

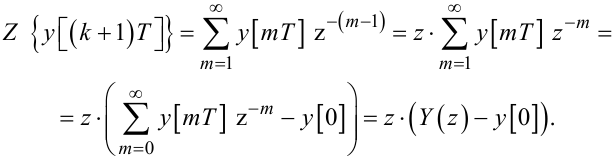(2.58)

Аналогічно:

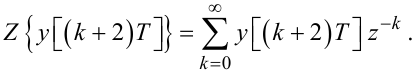(2.59)

Тепер нехай m = k + 2, тоді

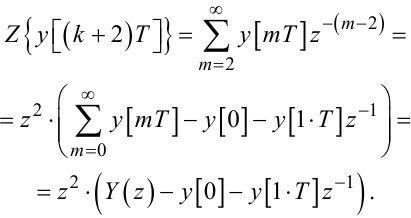(2.60)

Узагальнюючи (2.58) та (2.60), отримуємо для довільного n:

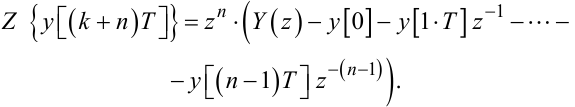(2.61)

Тепер розглянемо зсув вліво:

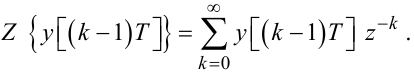(2.62)

Нехай k - 1 = m, тоді

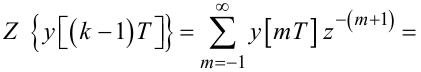(2.63)

Виводячи формулу (2.63), використано властивість оригіналу бути рівним нулю за від’ємних значеннях аргументу

Аналогічно:

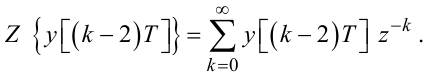(2.64)

Нехай k - 2 = m , тоді:

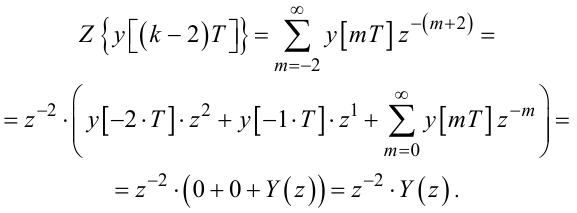(2.65)

Узагальнюючи (2.63) та (2.65), отримуємо для довільного n:

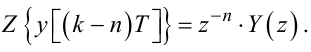(2.66)

Порівнюючи вирази (2.61) і (2.66), приходимо до висновку, що за допомогою Z-перетворення доцільніше розв’язувати різницеві рівняння, які конструюються із диференціальних шляхом застосування обернених скінченних різниць

Якщо ж різницеве рівняння сконструйоване із диференціального за допомогою прямих скінченних різниць, то його доцільніше розв’язувати рекурентною (крок за кроком) процедурою, аналогічною (2.38).

Нехай математична модель дискретної системи має вигляд:

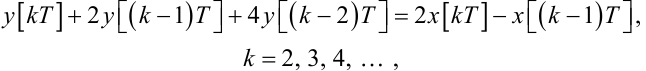(2.67)

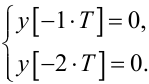(2.68)

Знайдемо Z-перетворення рівняння (2.67) за початкових умов (2.68).

Записуючи, спочатку формально,

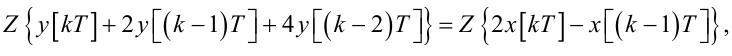(2.69)

та враховуючи лінійні властивості Z-перетворення (2.55), (2.56), отримаємо:

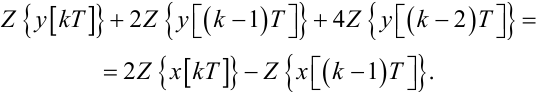(2.70)

Із (2.70) з урахуванням (2.52), (2.63), (2.65) випливає:

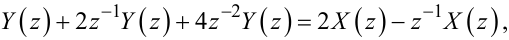(2.71)

або

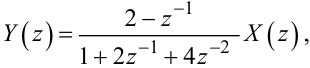(2.72)

або

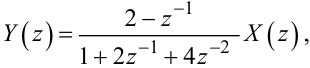(2.73)

де

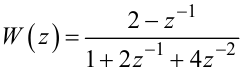(2.74)

— дискретна передаточна функція динамічної системи, що описується різницевим рівнянням (2.67).

Нехай x[kT] = 1[kT], тоді згідно з (2.54)

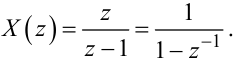(2.75)

Підставляючи (2.75) у (2.72), отримаємо:

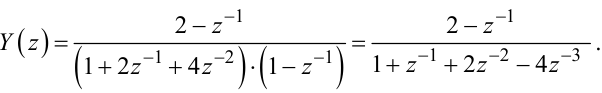(2.76)

Як і під час використання звичайного перетворення Лапласа, де для знаходження оригіналу за відомим зображенням використовується або процедура взяття оберненого інтеграла на основі теореми про лишки, або одна із формул розкладання, існує декілька процедур знаходження решітчастих оригіналів за їх відомим Z-зображенням. Але у практиці перевагу віддають найпростішій процедурі, яка полягає у діленні багаточлена на багаточлен.

Якщо розписати суму у формулі Z-перетворення в (2.52), то отримаємо:

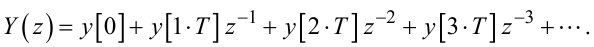(2.77)

Із виразу (2.77) видно, що коефіцієнти при степенях z^-k (k = 0,1,...) і є значеннями решітчастої функції y[kT], яка є оригіналом для Z-зображення Y(z).

А до форми (2.77) дробово-раціональна функція, яка є відношенням двох багаточленів, приводиться діленням чисельника на знаменник і взяттям такої кількості членів ряду, яка необхідна за умовами розв’язання

Застосуємо описану процедуру до виразу (2.76):

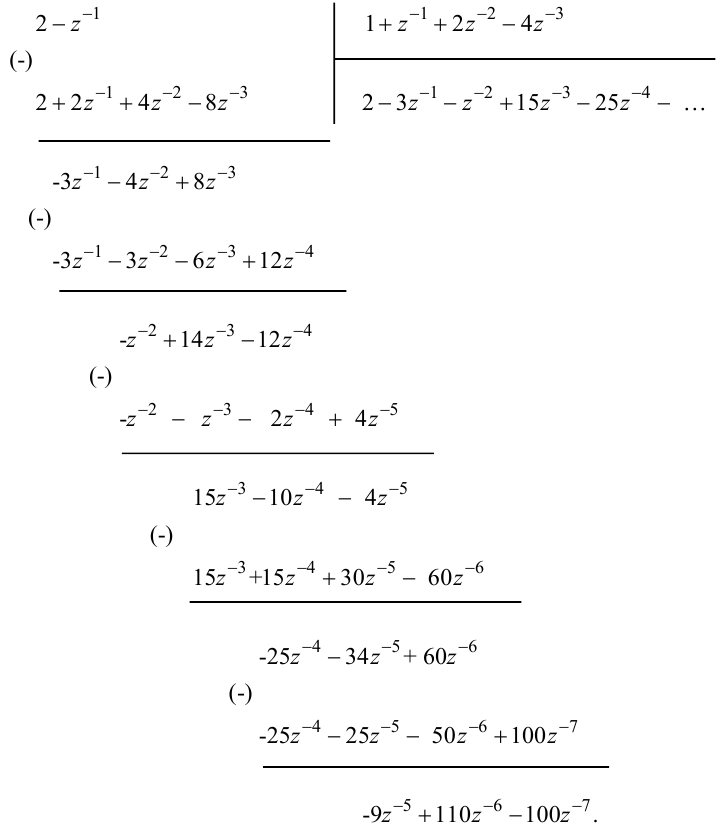Зупинившись на цьому кроці, Y(z), що задано виразом (2.76), можна записати у такий спосіб:

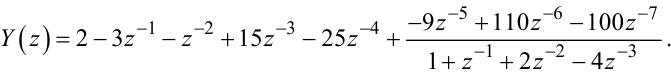(2.78)

Порівнюючи (2.77) та (2.78), знаходимо п’ять перших значень решітчастої функції y[kT], яка є оригіналом для Z-зображення Y(z), визначеного формулою (2.76):

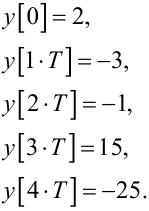(2.79)

Оскільки процес ділення багаточлена на багаточлен легко алгоритмізується, то на комп’ютері дуже швидко можна отримати яку завгодно сукупність значень решітчастого оригіналу, час отримання якої обмежується, фактично, лише часом виведення цієї сукупності значень за допомогою принтера на папір.