2.4 Математична модель комп’ютера як елемента дискретної детермінованої ЛДС ЗП

Відомо, що при складних законах управління навіть лінійними динамічними об’єктами стає доцільним використання комп’ютера в замкнутому контурі для формування цих законів. Найчастіше комп’ютери, на яких покладаються такі задачі, є спеціалізованими і реалізовними в мікропроцесорному варіанті.

Як відомо, цифри у мікропроцесорі формуються комбінаціями імпульсів, а сигнали до і після мікропроцесора є неперервними, а точніше — кусково-неперервними часовими функціями. Для узгодження характеристик неперервних та імпульсних процесів на вході мікропроцесора ставлять пристрій, котрий неперервні сигнали перетворює в комбінації імпульсів і називається аналого-цифровим перетворювачем (АЦП), а на виході мікропроцесора обов’язковим під час його використання в САЕП є підключення пристрою, який комбінації імпульсів перетворює в кусково-неперервний сигнал і називається цифроаналоговим перетворювачем (ЦАП). Спрощені функціональні схеми АЦП та ЦАП зображені на рис. 2.5 та 2.6

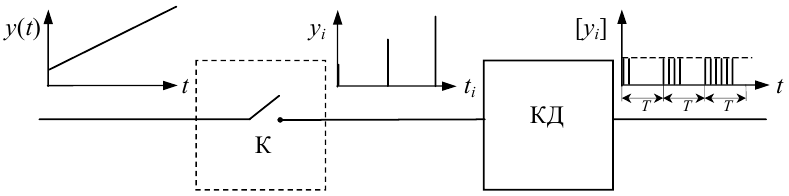
Рисунок 2.5 — Спрощена функціональна схема АЦП

Принципово АЦП (рис. 2.5) складається тільки з двох функціональних блоків. Перший блок — це ключ К, який, лише на мить один раз за період ча- су T вмикаючись, перетворює неперервний сигнал y(t) у послідовність імпульсів yi, для яких справедливо:

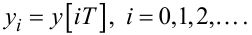(2.80)

Другий блок — це кодер КД, який кожному імпульсу y_i ставить у відповідність пачку імпульсів однакової амплітуди, кількість «n » яких у пачці однозначно залежить від значення амплітуди імпульсу y_i, тобто

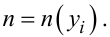(2.81)

З такими параметрами імпульсів однакової амплітуди вже може працювати мікропроцесор.

В результаті виконання мікропроцесором заданих операцій на його виході з’являються комбінації інших пачок імпульсів, котрі надходять на вхід цифроаналогового перетворювача ЦАП (рис. 2.6), який принципово складається лише з трьох функціональних блоків.

Рисунок 2.6 — Спрощена функціональна схема ЦАП

Перший блок — це декодер ДК, котрий кожній пачці з «m» імпульсів однакової амплітуди ставить у відповідність один імпульс xi, амплітуда якого однозначно відображає кількість «m» імпульсів у пачці, тобто

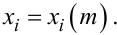(2.82)

Другий блок — фіксатор ФК, який запам’ятовує амплітуду xi імпульсу, що надходить з декодера ДК, на весь період T аж до появи наступного імпульсу x_i+1, перетворюючи послідовність імпульсів xi у кусково-сталу східчасту функцію . Динамічна характеристика фіксатора має вигляд, наведений на рис. 2.7, а математично може бути записаною у вигляді

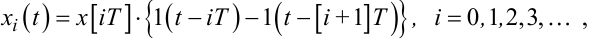(2.83)

де, нагадаємо, 1(t) — одинична східчаста функція.

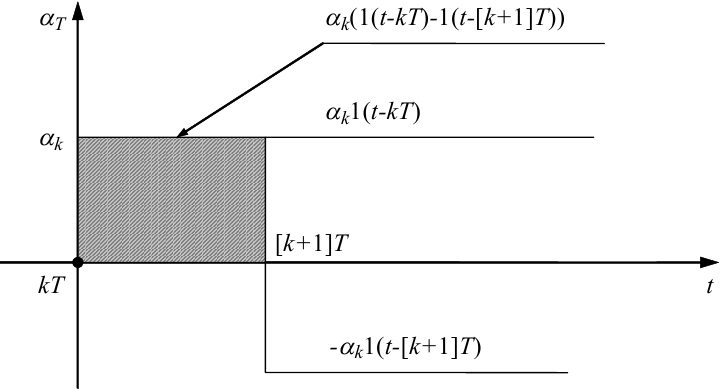
Рисунок 2.7 — Графік динамічної характеристики фіксатора

Третій блок ЦАП — фільтр Ф згладжує кусково-сталу східчасту функцію і перетворює її в неперервну функцію x(t).

Якщо використати алгоритм експоненціального згладжування, то модель згладженого сигналу x(t) на виході фільтра матиме вигляд

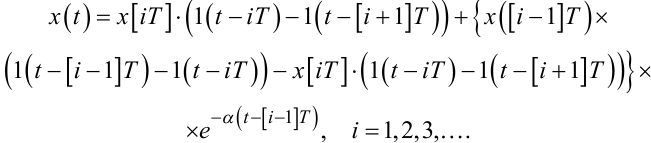(2.84)

Що стосується безпосередньо мікропроцесора, то він протягом відрізка часу τ реалізує задану програму, завдяки якій довільна функція y(t) перетворюється у функцію x(t) з заданими характеристиками.

Для прикладу розглянемо випадок, коли мікропроцесор формує сигнал x(t), який містить три складові: перша пропорційна координаті y(t), друга пропорційна її першій похідній ý(t), а третя — її другій похідній ÿ(t), тобто

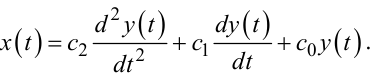(2.85)

Але, оскільки мікропроцесору для реалізації залежності (2.85) потрібен певний час τ, протягом якого він отримує результат і не видає нічого на ЦАП, то рівняння (2.85) недостатньо для того, щоб задати модель мікропроцесора у загальній математичній моделі динамічної системи. Його потрібно доповнити ще рівнянням блока затримки сигналу на час τ, тобто рівнянням

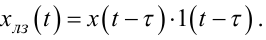(2.86)

Після цього зробимо два важливі зауваження. Перше з них полягає в тому, що не треба думати начебто якимсь одним рівнянням, наприклад (2.85), можна раз і назавжди задати математичну модель мікропроцесора. Вона змінюватиметься кожний раз, коли зазнаватиме змін та функція, реалізація якої покладатиметься на мікропроцесор.

Друге зауваження полягає в тому, що рівняння (2.85) стає непридатним для моделювання процесів у системі, якщо розглядається не лише характер процесів у її безперервній частині, а й характер процесів в імпульсних елементах системи, наприклад у ЦАП чи АЦП.

У цьому випадку від диференціального рівняння як математичної моделі мікропроцесора слід переходити до рівняння в скінченних різницях, що для прикладу зробимо саме для моделі (2.85), використавши обернені скінченні різниці.

Використовуючи для перетворення диференціального рівняння (2.85) на основі обернених скінченних різниць процедуру, викладену у співвідношеннях (2.27) — (2.32) для прямих скінченних різниць, отримаємо

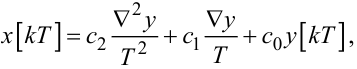(2.87)

або

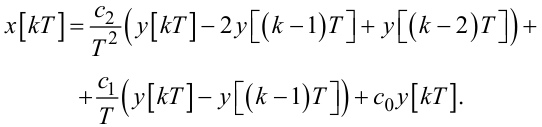(2.88)

або

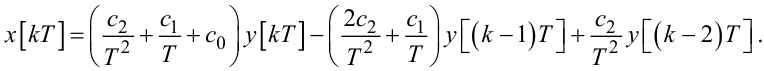(2.89)

Якщо покласти, що для часу τ, який використовується мікропроцесором для розрахунку вихідної координати закладеної в нього моделі, наприклад, (2.85), справедливою є рівність

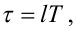(2.90)

де l — ціле число, то за дискретний аналог рівняння блока затримки (2.86) матимемо

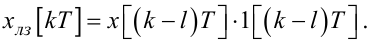(2.91)

На завершення цього підрозділу зауважимо і звернемо увагу на те, що у функціональній схемі динамічної системи, яка використовує мікропроцесор, кодер АЦП і декодер ЦАП слід відносити до функціональної схеми мікропроцесора, за межами якої виноситься від АЦП лише ключ, котрий із неперервної вхідної функції формує решітчасту, а від ЦАП за межі функціональної схеми мікропроцесора виноситься фіксатор, який із решітчастої вихідної функції формує неперервну кусково-сталу, та фільтр, який неперервну кусковосталу функцію перетворює у неперервну гладку.

У загальній математичній моделі такої динамічної системи ці блоки враховуються їх моделями, визначеними виразами (2.80), (2.83) та (2.84).

Але якщо кінцевою моделлю динамічної системи є сукупність різницевих рівнянь, що описують усі структурні блоки цієї системи, то враховувати