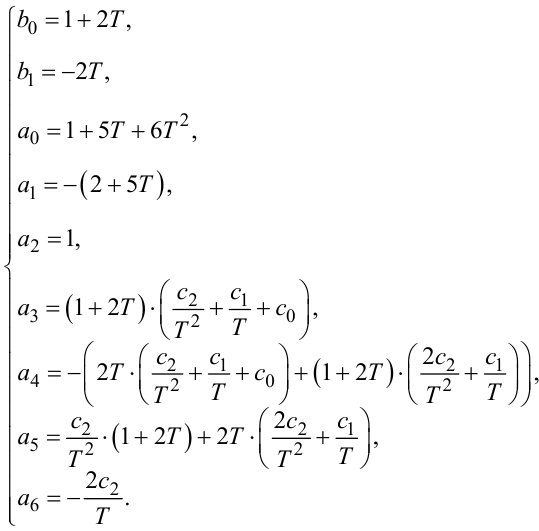2.5 Приклад побудови математичної моделі детермінованої дискретної ЛДС ЗП

Нехай за допомогою мікропроцесорного регулятора (МПР), який реалізує закон регулювання, що представлений залежністю (2.85), здійснюється управління детермінованим лінійним динамічним об’єктом (ЛДО), про який відомо лише те, що його реакцією на вхідний сигнал x(t) у вигляді одиничної східчастої функції (1.9) є вихідний сигнал y(t) у вигляді залежності (1.41), в якій покладемо, що f(t) = y(t). Функціональна схема цієї системи управління наведена на рис. 2.8.

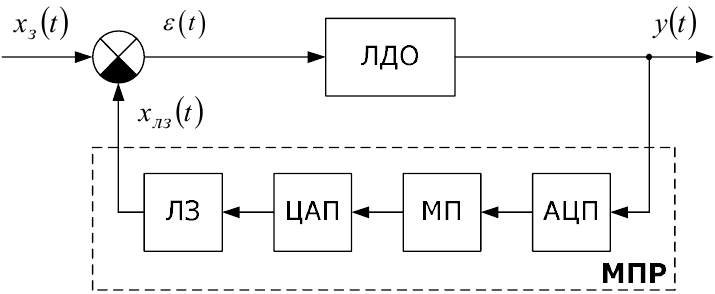
Рисунок 2.8 — Функціональна схема мікропроцесорної системи управління детермінованим лінійним динамічним об’єктом

На цій схемі для функціональних блоків АЦП і ЦАП прийняті такі ж позначення, як і на схемах рисунків 2.5 і 2.6, а символом ЛЗ позначена лінія затримки на час τ, потрібний мікропроцесору для визначення координати управління згідно з закладеним в нього законом (2.85).

Побудуємо математичну модель цієї дискретної детермінованої ЛДС ЗП як в часовій області у вигляді системи різницевих рівнянь, так і на комплексній площині у вигляді дискретної передаточної функції.

Почнемо з побудови моделей об’єкта управління ЛДО, передаточну функцію якого W(p) знайдемо за допомогою виразу (1.30), підставивши в нього перетворені за Лапласом вхідний та вихідний сигнали,

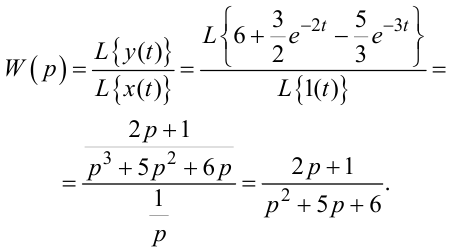(2.92)

Зауважимо, що при отриманні виразу (2.92) використано отримані раніше зображення функцій (1.9) та (1.41) у вигляді (1.17) та (1.36).

Підставляючи (2.92) в (1.30), після нескладних перетворень отримаємо:

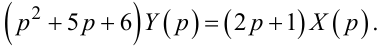(2.93)

З викладеного раніше випливає, що рівнянню (2.93) в області зображень в області оригіналів буде відповідати диференціальне рівняння

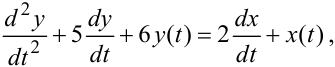(2.94)

якому, у свою чергу, відповідатиме рівняння в кінцевих обернених різницях

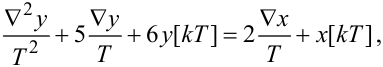(2.95)

де T — період, з яким ключ АЦП із неперервної функції y(t) формує решітчасту y[kT], а декодер ЦАП із пачок імпульсів, що надходять з мікропроцесора, формує решітчасту функцію x[kT].

Використовуючи раніше викладену методику, тобто розписуючи в рівнянні (2.95) обернені різниці через значення решітчастої функції та впорядковуючи отримані результати, різницевим аналогом цього рівняння матимемо

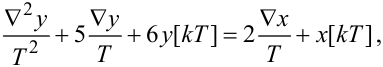(2.96)

Різницеве рівняння (2.96) задає дискретну математичну модель об’єкта управління дискретної динамічної системи, а різницеві рівняння (2.89) та (2.91), побудовані у попередньому підрозділі, задають дискретну математичну модель мікропроцесорного регулятора цієї системи, включеного в контур зворотного зв’язку. Очевидно, що для побудови замкнутої математичної моделі динамічної системи, що розглядається, придатної для її аналізу і оптимізації, необхідно систему різницевих рівнянь (2.96), (2.89), (2.91) доповнити ще одним різницевим рівнянням, яке задасть дискретну математичну модель компаратора на вході ЛДО, котрий має два входи: один для заданого сигналу x₃(t), котрий об’єкт управління повинен відпрацьовувати, а другий для сигналу x_лз(t), котрий надходить по контуру зворотного зв’язку з мікропроцесорного регулятора, та один вихід, з якого на об’єкт управління подається відхилення ε(t), яке виникає в процесі роботи системи між сигналами x_з(t) та x_лз(t).

Виходячи з логіки роботи компаратора, можна одразу записати, що

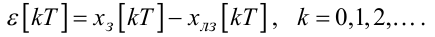(2.97)

Цілком очевидно, що для замикання математичної моделі дискретної динамічної системи, заданої різницевими рівняннями (2.89), (2.91), (2.96), (2.97), у правій частині рівняння (2.96) необхідно замість підставити відповідно .

Тепер побудуємо математичну модель цієї ж дискретної динамічної системи на комплексній площині. Для цього здійснимо Z-перетворення різницевих рівнянь (2.89), (2.91), (2.96), (2.97).

Перетворюючи (2.89), отримаємо

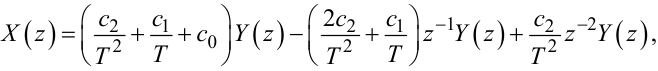(2.98)

або

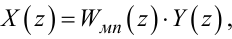(2.99)

де

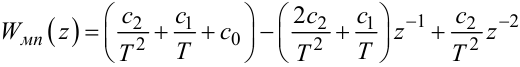(2.100)

— дискретна передаточна функція мікропроцесора МП

Перетворюючи (2.91), отримаємо

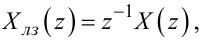(2.101)

або

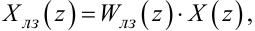(2.102)

де

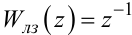(2.103)

— дискретна передаточна функція лінії затримки ЛЗ.

Перетворюючи (2.96) з врахуванням зробленого вище зауваження стосовно його правої частини, отримаємо

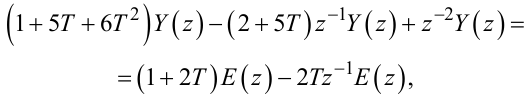(2.104)

або

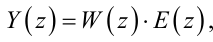(2.105)

де

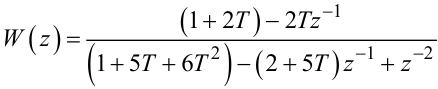(2.106)

— дискретна передаточна функція об’єкта управління ЛДО.

Перетворюючи (2.97), отримаємо

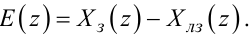(2.107)

Структурна схема динамічної системи, дискретні передаточні функції структурних блоків якої задані виразами (2.100), (2.103), (2.106), (2.107), наведена на рис. 2.9.

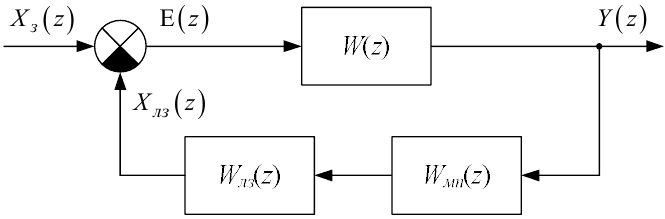
Рисунок 2.9 — Структурна схема детермінованої дискретної ЛДС ЗП, взятої для прикладу

Якщо потрібно отримати математичну модель даної системи як перетворювача заданого сигналу x_з(t) у вихідний сигнал y(t) у вигляді

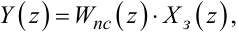(2.108)

де W_пс(z) — дискретна передаточна функція системи як перетворювача (рис. 2.10), то з рівнянь (2.99), (2.102), (2.105), (2.107) необхідно вилучити шляхом послідовної підстановки усі проміжні змінні, залишивши лише вхідну координату X_з(z) та вихідну координату Y(z).

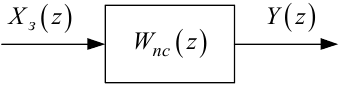
Рисунок 2.10 — Структурна схема взятої для прикладу детермінованої дискретної ЛДС ЗП як перетворювача сигналу

В результаті цих перетворень отримаємо

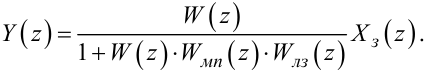(2.109)

Підставляючи в (2.109) вирази для передаточних функцій із (2.100), (2.103), (2.106), виконуючи необхідні перетворення та порівнюючи отриманий результат з виразом (2.108), отримаємо

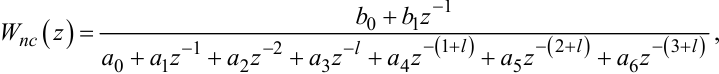(2.110)

де: