8.1 Математичні моделі нелінійних динамічних систем, статичні характеристики яких допускають лінеаризацію

Класичним і надзвичайно розповсюдженим прикладом нелінійних динамічних систем, статичні характеристики яких допускають лінеаризацію, є системи з електромеханічним перетворенням енергії, обов'язковою складовою яких є електромагнітні підсистеми. Цими складовими можуть бути електродвигуни, електричні генератори, електромагнітні муфти, магнітні підси-лювачі, тягові соленоїди та інші елементи, характерною особливістю яких є наявність котушки індуктивності, намотаної на сталеве осердя.

Спільним для всіх цих елементів електромеханічної системи є те, що їх характеристики намагнічування, які є залежністю магнітного потоку Ф в осерді від струму I в обмотці, мають вигляд, наведений на рис. 8.1.

Рисунок 8.1 — Графік характеристики намагнічування Ф = f(I) електромагнітної системи

Із цього рисунка видно, що лінійною характеристику намагнічування Ф = f(I) можна вважати лише при значеннях струму I в обмотці, які не перевищують I_Л. А при I > I_Л магнітна система починає насичуватись, і магнітний потік Ф в сталевому осерді хоча й збільшується зі зростанням струму I, але не пропорційно значенням струму.

Тож, якщо елемент електромеханічної системи з характеристикою намагнічування Ф = f(I), наведеною на рис. 8.1, працює при значеннях струму в обмотці I < I_Л, то система з таким елементом буде належати до класу лінійних, і для математичного моделювання процесів в ній можна використовувати весь той математичний апарат, який наведено в попередніх двох частинах даного навчального посібника.

Але, якщо цей же елемент працює при значеннях I > I_Л, наприклад, при I = I_H, то лінійною його характеристику намагнічування вже вважати не можна, оскільки, якщо її вважати лінійною, це означатиме, що при I = I_H магнітний потік Ф в осерді повинен бути рівним Ф, в той час як насправді він дорівнює Ф_H (див. рис. 8.1).

Оскільки аналіз процесів в лінійних системах є найбільш простим і узагальненим, то плавні аналітичні нелінійності типу «насичення» намагаються «покрити» відрізками прямих так, щоб цих відрізків було найменше при допустимих значеннях похибок заміни реальної нелінійної кривої ламаною, складеною з відрізків прямих. Процес заміни плавних нелінійностей ламаними лініями, що складаються з відрізків прямих, називають їх лінеаризацією.

Приклад такого «покриття», тобто лінеаризації, наведено на рис. 8.2, на якому крива 0 - a - b - c - d замінюється ламаною 0 - a^* - b^* - c^* - d^*, тобто вона «покривається» трьома відрізками 0 - a^*, a^* - c^*, c^* - d прямих.

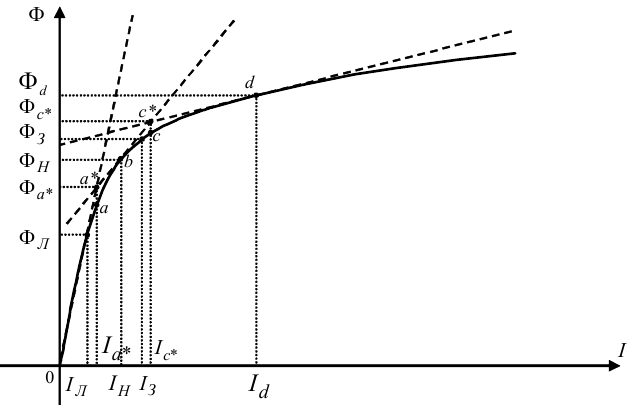
Рисунок 8.2 — Варіант «покриття» кривої намагнічування Ф = f(I) відрізками прямих

У цьому випадку під час аналізу процесів, що протікають в даному елементі електромеханічної системи, при значеннях струму I < I_Л як характеристику намагнічування Ф = f(I) будемо використовувати відрізок прямої 0 - a^*, при значеннях струму I_Л ≤ I < I₃ — відрізок прямої a^* - c^*, а при значеннях струму I₃ < I — відрізок прямої c^* - d.

Очевидно, що такою заміною кривої намагнічування ламаною лінією будемо мати певну похибку моделювання, найбільші значення якої досягатимуться в точках .

Але якщо в усталеному режимі роботи елемент працює в точці (I_H, Ф_H), то з рис. 8.2 легко побачити, що у цій точці похибка моделювання дорівнюватиме нулю.

Тож виходить, що кускова лінеаризація плавної нелінійної характеристики елемента електромеханічної системи, допускаючи певну похибку при моделюванні перехідних процесів, дозволяє звести цю похибку до нуля при математичному моделюванні усталеного режиму.

Якщо елемент електромеханічної системи працює здебільшого не в номінальному (I_H, Ф_H), а в якомусь іншому режимі, наприклад, (I₃, Ф₃), то підхід залишається тим же, однак в цьому випадку точку «b» ламаної суміщаємо з точкою (I₃, Ф₃) кривої.

Три важливих зауваження:

1. Під час математичного моделювання нелінійних динамічних систем з елементами, що мають аналітичні нелінійні характеристики типу наведених на рис. 8.1 та рис. 8.2, необхідно не забувати «зшивати» рішення сусідніх математичних моделей в моменти часу, коли процес, що моделюється, входить в точки стику ламаних, якими лінеаризується нелінійна характеристика.

2. Якщо моделюється нелінійна динамічна система з регулятором, що не допускає суттєвих відхилень процесу від заданого режиму роботи, то при моделюванні усталеного режиму такої системи та близьких до нього перехідних режимів завжди достатньо враховувати лише один лінійний відрізок ламаної, що «покриває» нелінійність в області, для якої точка заданого режиму є внутрішньою. При цьому чим більшим є коефіцієнт підсилення регулятором вхідного сигналу, тим меншою буде похибка моделювання, оскільки з ростом коефіцієнта підсилення регулятора звужується область відхилення робочої точки на нелінійній характеристиці елемента системи від точки заданого режиму.

3. Кусково-лінійна апроксимація нелінійної характеристики елемента системи в загальному вигляді y = f(x) непридатна для використання в задачах оптимізації цієї системи аналітичними методами, оскільки в точках стику ламаної перша похідна має розрив 1-го роду, а другої похідної не існує взагалі, в той час як аналітичні методи оптимізації вимагають існування як 1-ої, так і 2-ої похідних нелінійної характеристики перетворення в усіх точках області оптимізації.