8.2.1 Вихідні умови та постановка задачі

Досить широкому класу динамічних систем в хімічній технології та теплоенергетиці з вхідним впливом x(t) та реакцією на нього y(t), динаміка яких характеризується імпульсною перехідною характеристикою g(t), притаманна статична характеристика y = f(x), яка має екстремальний характер (рис. 8.3)

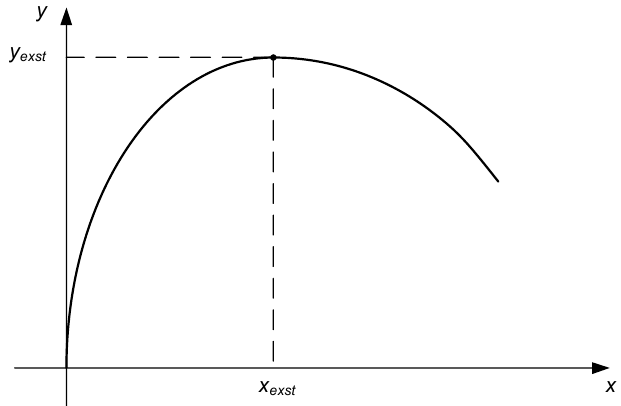
Рисунок 8.3 — Екстремальна статична характеристика нелінійної динамічної системи

Тож, щоб повністю ідентифікувати таку нелінійну систему, необхідно визначити обидві ці характеристики і g(t), і y = f(x).

Саме така задача і ставиться.

Для розв'язання цієї задачі висунемо дві вихідні передумови, згідно з першою з яких пропонується ідентифікувати статичну нелінійну характеристику y = f(x) системи степеневим поліномом третього порядку, тобто

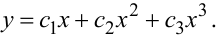(8.1)

Звичайно, для апроксимації екстремальної статичної характеристики, наведеної на рисунку 8.3, можна використати і степеневий поліном другого порядку, оскільки у нього точка екстремуму буде мати такі ж самі координати (x_exst, y_exst), але використаємо степеневий поліном третього порядку, тому що він точніше передає характер наростання координати y при початкових значеннях координати x.

А як другу вхідну передумову використаємо відомий підхід, оснований на тому, що структура динамічної системи розглядається у вигляді послідовного з'єднання її інерційної лінійної частини з імпульсною перехідною характеристикою g(t) і проміжним вихідним сигналом x^*(t) та нелінійної безінерційної ланки з характеристикою y = f(x^*) (рис. 8.4)

Рисунок 8.4 — Структура нелінійної динамічної системи з виділенням інерційної лінійної частини та безінерційної нелінійної частини

Очевидно, що після введення другої вихідної умови в рівнянні (8.1) потрібно замість x розглядати x^*.