8.2.2 Ідентифікація нелінійної статичної характеристики

Як відомо, вихідний сигнал x^*(t) лінійної частини нелінійної динамічної системи можна знайти за допомогою інтеграла згортки

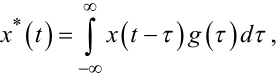(8.2)

який за умови фізичної реалізовності цієї системи

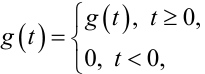(8.3)

набуває вигляду

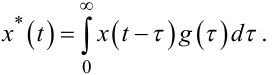(8.4)

Згідно з теорією Фур'є-інтегрального методу ідентифікації динамічних систем розкладемо вхідний сигнал x(t) у відрізок ряду Фур'є на вибраному проміжку часу T . В результаті цього матимемо

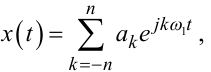(8.5)

де a

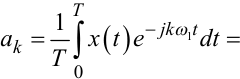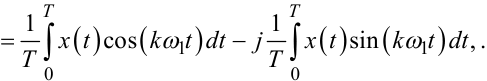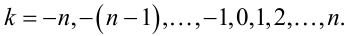(8.6)

Одразу ж відзначимо, що при формуванні якогось сигналу фізичної системи з обмеженим запасом енергії, він завжди може бути апроксимований з заданою точністю відрізком ряду Фур'є.

Підставляючи значення x(t) з виразу (8.5) у вираз (8.4), отримаємо

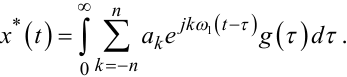(8.7)

або

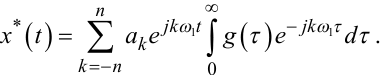(8.8)

Якщо згадати, що передаточна функція лінійної частини нелінійної динамічної системи — це

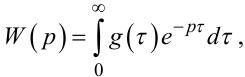(8.9)

а її амплітудно-фазова частотна характеристика (АФЧХ) — це

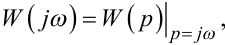(8.10)

то рівняння (8.8) нескладно привести до вигляду

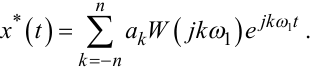(8.11)

Підставляючи значення x^*(t) з виразу (8.11) у вираз (8.1) матимемо

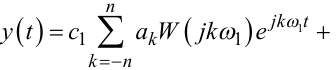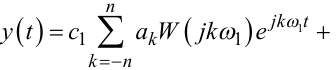(8.12)

В разі якщо вхідний сигнал x(t) являє собою синусоїду з частотою ω₁, тобто

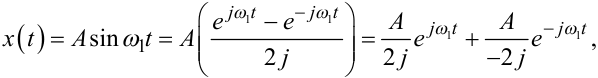(8.13)

рівняння (8.12) перетвориться на рівняння

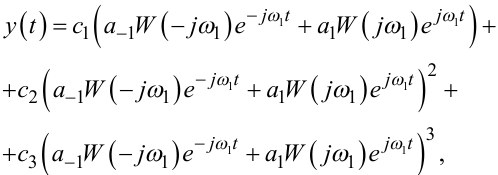(8.14)

у якому

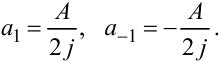(8.15)

Підносячи до степеня в рівнянні (8.14) і групуючи члени з однаковими гармонічними складовими, отримаємо

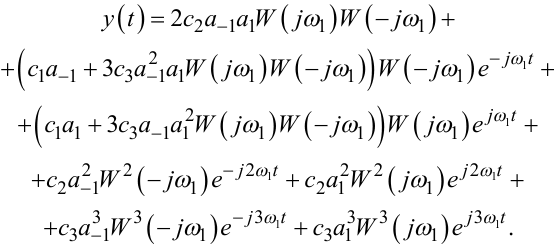(8.16)

Тепер розкладемо у відрізок ряду Фур'є на тому ж проміжку часу T вихідний сигнал y(t), який є реакцією динамічної системи на вхідну синусоїду, тобто подамо його у вигляді

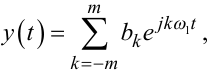(8.17)

де 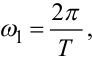a

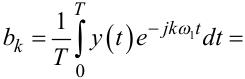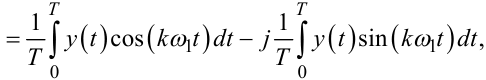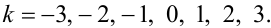(8.18)

Оскільки у правій частині рівняння (8.16) маємо лише сталу складову і гармоніки з частотами -3ω₁, -2ω₁, -ω₁, ω₁1, 2ω₁, 3ω₁, то зрізаний ряд (8.17) для реакції y(t) системи на синусоїду частоти ω₁ теж буде мати лише ці складові — саме тому значення k при визначенні коефіцієнтів Фур'є b_k задані лише в межах від –3 до 3.

Підставляючи значення y(t) з виразу (8.17) при m = 3 у рівняння (8.16), отримаємо тотожність, яка виконуватиметься лише тоді, коли коефіцієнти Фур'є при однакових гармоніках у правій та лівій частинах цієї тотожності будуть рівними.

Завдяки цьому отримаємо таку систему рівнянь

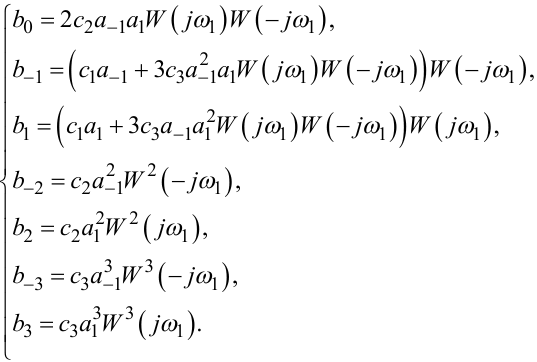(8.19)

З шостого та сьомого рівнянь цієї системи знайдемо, що

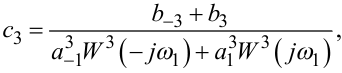(8.20)

з четвертого та п'ятого рівнянь отримаємо

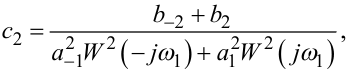(8.21)

а з другого та третього —

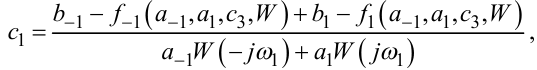(8.22)

де

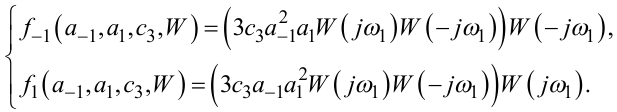(8.23)

Як бачимо, перше рівняння системи (8.19) є надлишковим, тож його можна використати як критерій правильності розв'язання задачі.

Ще одним критерієм правильності розв'язання задачі може служити поява суттєво відмінних від нуля значень коефіцієнтів Фур'є з номерами k > 3 та -k < -3 у вихідному сигналі y(t) при його розкладенні в ряд (8.17) за умови, що на вхід системи надходить лише синусоїда однієї частоти ω₁. Це означатиме, що реальна статична характеристика y(x) об'єкта повинна апроксимуватись степеневим поліномом з порядком вище 3-го. При наявності гармонік з частотою 4ω₁ та -4ω₁ в сигналі y(t) для апроксимації характеристики y = f(x) поліном потрібно брати 4-го порядку, а при наявності гармонік з частотою 5ω₁ та -5ω₁ цей поліном повинен мати 5-ий порядок, і далі за зростанням.

Слід зазначити, що підвищення порядку полінома для апроксимації характеристики y = f(x) не надто ускладнює отримання виразів для розрахунку коефіцієнтів цього полінома за умови використання на вході об'єкта синусоїди лише однієї частоти, оскільки для отримання співвідношень виду (8.19) і в цьому випадку в виразі виду (8.14) степені розкриваються за формулою бінома Ньютона

Із співвідношень (8.20), (8.21), (8.22) випливає, що ідентифікувати екстремальну статичну характеристику y = f(x) нелінійної динамічної системи класу, що розглядається, можна лише за умови, що є відомими значення АФЧХ W(jω) лінійної інерційної частини цієї системи на частотах ω₁ та -ω₁, тобто відомими є W(jω₁) та W(-jω₁). Тож далі піде мова про те, як знайти ці значення.