8.2.3 Ідентифікація лінійної інерційної частини нелінійної динамічної системи

З фізики будь-якої динамічної системи випливає, що допоки її масовий чи енергетичний об'єм не наповниться масою чи енергією, які надходять разом із вхідним впливом, принаймні, наполовину, доти процеси в цій системі наростають лінійно за винятком близької до нуля зони нечутливості або люфту.

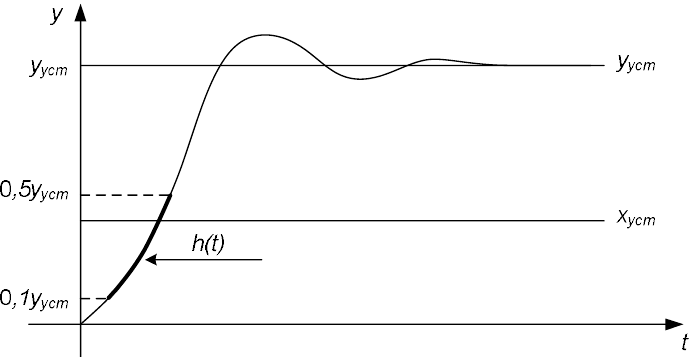
Рисунок 8.5 — Графік перехідного процесу в динамічній системі після подачі на її вхід сходинкового впливу на рівні його усталеного значення

Тож, якщо сформувати вхідний вплив на нелінійну систему так, щоб його рівень відповідав усталеному рівню реакції цієї системи на прикладений вхідний вплив (рис. 8.5), то можна стверджувати, що в діапазоні значень вихідної координати y(t) від 0,1y_уст до 0,5y_уст система вестиме себе як лінійна.

І якщо вхідний вплив подається стрибком від 0 до xуст, то у вказаному діапазоні значень y(t) вихідна координата буде збігатися з перехідною характеристикою h(t) лінійної частини цієї системи, яка для системи з одним об'ємом концентрації енергії чи маси має вигляд:

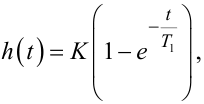(8.25)

або

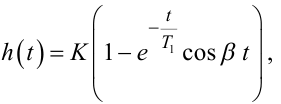(8.26)

а для об'єкта з трьома об'ємами концентрації енергії чи маси —

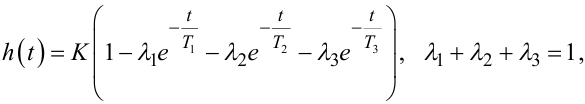(8.27)

або

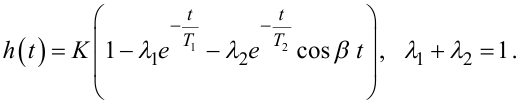(8.28)

Для більшої кількості об'ємів концентрації енергії чи маси ряд апроксимативних функцій для h(t) можна продовжити, користуючись тим самим принципом, але в цьому немає необхідності, оскільки в задачах синтезу систем екстремального регулювання передаточну функцію лінійної частини нелінійної динамічної системи немає сенсу брати вище третього порядку, адже екстремальний регулятор робочу точку від точки екстремуму далеко не відпускає.

Тож для апроксимації h(t) у вигляді (8.24) потрібно з кривої y(t) (див. рис. 8.5) скористатись двома точками в діапазоні 0,1y_уст ≤ y(t) ≤ 0,5y_уст для визначення параметрів K, T₁. Очевидно, що їх можна знайти з системи рівнянь

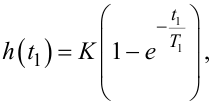(8.29)

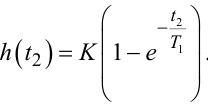(8.30)

Для апроксимації h(t) у вигляді (8.26) для визначення параметрів K, T₁ та β потрібно скористатись уже трьома точками з цього ж діапазону [0,1y_уст; 0,5y_уст]. Для них система рівнянь матиме вигляд

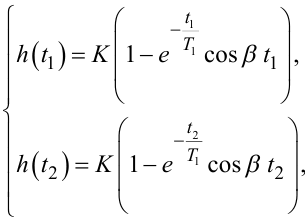(8.31)

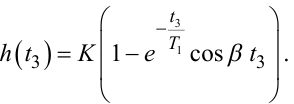(8.32)

У такий же спосіб можна розрахувати параметри всіх інших апроксимацій характеристики h(t).

Після цього необхідно, скориставшись кількома (наприклад, M) точками діапазону [0,1y_уст; 0,5y_уст] з індексом l, розрахувати для всіх знайдених апроксимацій h_i(t), i = 1,r середній квадрат Δ_i похибки апроксимації за виразом

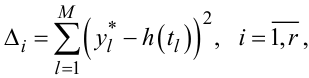(8.33)

де y_l^* — значення перехідної характеристики, взяте з експериментального графіка (див. рис. 8.5), а h(t_l) — значення цієї характеристики, вирахуване за апроксимувальним виразом.

Те з чисел Δ₁,Δ₂,...,Δ₁, яке буде найменшим, і визначатиме найкращу апроксимацію перехідної характеристики h(t) лінійної частини динамічної системи за критерієм мінімуму суми квадратів похибок на «свіжих» точках.

Знаючи перехідну характеристику h(t) лінійної частини об'єкта, легко знайти її передаточну функцію W(p), адже

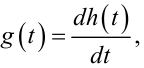(8.33)

а для отримання W(p) за відомою g(t) потрібно скористатись виразом (8.9).

В свою чергу значення W(jω₁) та W(-jω₁), які потрібні нам для ідентифікації екстремальної статичної характеристики y = f(x), отримаємо прямою підстановкою у вираз для передаточної функції W(p), отриманий за перетворенням (8.9), замість оператора p значень jω₁ та -jω₁.

Звичайно, якщо після кількох однотипних експериментів з подачею на вхід об'єкта однакового рівня вхідного впливу сходинкового характеру отримаємо експериментальні криві y(t), які не збігатимуться у діапазоні [0,1y_уст; 0,5y_уст], то параметри апроксимацій h(t) у вигляді (8.24) – (8.28) слід обчислювати, користуючись стандартною процедурою методу найменших квадратів.