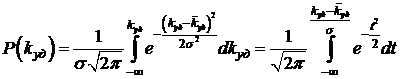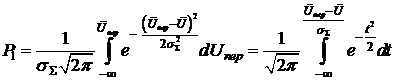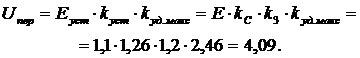5 Комутаційні перенапруги в електричних системах

5.8 Ударний коефіцієнт при комутаціях

Розвиток комутаційних перенапруг пов’язаний з рядом факторів, що мають статистичний характер. До таких факторів належать: власна частота мережі в момент комутації, фаза комутації, виникнення повторних пробоїв чи зрізів струму у вимикачах тощо. Внаслідок такого зв’язку самі комутаційні перенапруги, а точніше їх кратність, мають статистичний характер. Із цієї причини комутаційні перенапруги характеризуються кривими ймовірності, побудова яких базується на масових вимірюваннях в електричних мережах.

Дослідження комутаційних перенапруг на лініях показали, що ударні коефіцієнти при комутаціях мало залежать від схем мережі і довжини ліній і статистично розподіляються у відповідності з нормальним законом:

.      (5.10)

Для кожного виду комутації, як і для всіх комутацій в цілому, можуть бути вказані середні значення  та дисперсія . Найбільші значення , які слід практично враховувати, визначаються правилом трьох сигм:

.

У табл. 5.1 наведені значення  та  для різних комутацій.

Маючи параметри розподілення комутаційних перенапруг  і розрядних напруг ізоляції при комутаційних імпульсах , можна порахувати число перекритів ізоляції на лінії  при заданому числу комутацій n_к:

,

де

;     (5.11)

;

m – число ізоляційних проміжків на лінії.

Таблиця 5.1 – Параметри статистичних розподілів ударних коефіцієнтів

* Примітка:  – коефіцієнт остаточної напруги на ПЛ

Приклад 5.4 Визначити для умов комутації при ТАПВ, вказаних в прикладі 5.2, максимальне значення  у відповідності з правилом двох сигм.

При  = 0,4 с коефіцієнт = 0,6. За формулою, наведеною у п. 3 табл. 5.1:

=1,57 + 0,55·0,6 = 1,9

та

 =1,9 + 2·0,28 = 2,46.

Максимальна перенапруга рівна:

Це є дуже висока перенапруга. При виборі ізоляції ПЛ орієнтуються на значення, близькі до середніх, а не максимальних значень.