Дрейфовий планарно-епітаксійний n-p-n-транзистор.

Розрахунок дрейфового планарно-епітаксійного транзистора розглянемо на прикладі кремнієвого n⁺-p-n-n⁺-транзистора. Розподіл домішок в такому транзисторі подано на рис. 2.5, б, а його структура і топологія – на рис. 2.6.

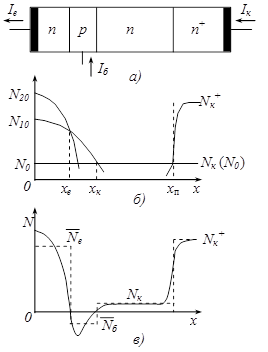
Рисунок 2.5 – Розподіл домішок в кремнієвому n⁺-p-n-n⁺ планарно-епітаксійному транзисторі

Для створення n⁺-p-n-n⁺ структури в епітаксійну плівку n-типу, що вирощена на сильно легованій n⁺-підкладці, проводять локальну двостадійну дифузію акцепторної домішки (бора) з низькою поверхневою концентрацією для створення області бази p-типу. Потім проводять локальну двостадійну дифузію донорної домішки (фосфору) для формування області емітера n⁺-типу. Межі емітерного і колекторного р-n-перехдів виходять на поверхню пластини під пасивуючою плівкою діоксиду кремнію. Профіль дифузійного розподілу домішки в активній області структури задається виразами:

N(x) = N₂(x) - N₁(x) + N₀ ;
N₂(x) = N₂₀exp(-k₂x²) ;
N₁(x) = N₁₀exp(-k₁x²) ;

де N₂₀ – поверхнева концентрація донорної домішки (фосфору);
N₁₀ – поверхнева концентрація акцепторної домішки (бору);
N₀ – вихідна концентрація донорної домішки в високоомному епітаксійному шарі колектора.

Задано

1. Електрофізичні параметри шарів кремнію: концентрація легуючих домішок N_20, N_10, N₀ ; концентрація донорної домішки в n⁺-підкладці N_п; час життя неосновних носіїв заряду в указаних шарах.

2. Геометричні розміри і топологія структури: глибина залягання емітерного х_е і колекторного х_к р-n-переходів, товщина вихідного епітаксійного n-шару х_п, товщина підкладки ω_п; довжина l_е і ширина z_е емітерної смужки; довжина l_к і ширина z_к колектора; розміри смужок базової металізації l_б і z_б. Будемо вважати, що всі зазори, які визначають відстані від краю емітера до металізації бази та від краю емітера до краю колектора, складають Δ.

3. Робоча напруга на колекторі U_к = -5 В, струм емітера І_е = 1 мА.

4. Температура Т = 300 К.

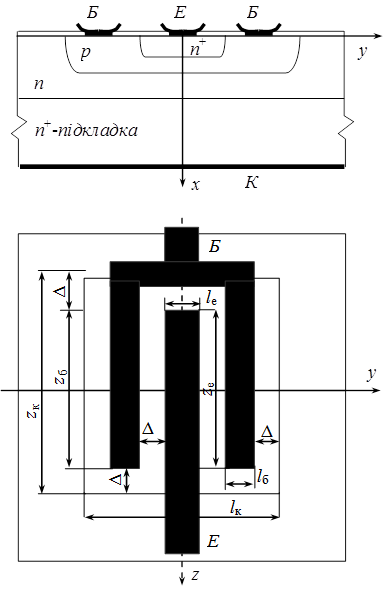
Рисунок 2.5 – Структура та топологія кремнієвого n⁺-p-n-n⁺ планарно-епітаксійного транзистора

Електрофізичні параметри і геометричні розміри транзистора зведені в табл. 2.3.

Рухливість основних і неосновних носіїв заряду зменшується зі зростанням сумарної концентрації іонізованих атомів легуючої домішки N⁺(х) і може бути розрахована за емпіричною формулою. Величина N⁺(x) визначається модулем суми позитивних і негативних іонізованих атомів легуючої домішки: N⁺(x) = N₂(x) + N₁(x) + N_0.

Наведені в табл. 2.3 значення часу життя неосновних носіїв заряду в областях структури розраховані за умови, що рекомбінація електронів і дірок відбувається на рекомбінаційних пастках, утворених атомами золота, концентрація яких постійна по всій структурі і становить: N_t = N_Au = 0,1 N₀ = 10¹⁵ см^-3.

При іншій концентрації золота час життя електронів і дірок може бути розраховано за формулами;
;

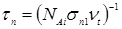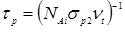
де σ_n1 = 6,3·10^-15 см² - переріз захоплення електрона; σ_p2 = 11,5·10^-15 см² - переріз захоплення дірки на рекомбінаційну пастку; υ_t ≈ 10⁷ см/с - теплова швидкість носіїв заряду при 300 К.

Визначити

1. Значення констант к₁ і к_2, пов'язаних з параметрами дифузії домішки. Розрахувати розподіл домішок в структурі N₂(x), N₁(x), N(x), N⁺(x).

2. Електрофізичні параметри шарів напівпровідника: залежність рухливості носіїв заряду від координати; середні значення рухливості і дифузійної довжини неосновних носіїв заряду в шарах; середній питомий опір і питомий поверхневий опір кожного шару.

3. Параметри еквівалентної схеми транзистора для великого сигналу.

4. Параметри фізичної Т-подібної еквівалентної схеми транзистора, та h-параметри транзистора із спільною базою і спільним емітером.

5. Максимально допустимі параметри транзистора.

Порядок розрахунку

На додаток до даних табл. 2.3 приймемо концентрацію донорів в n⁺-підкладці N_п = 10²⁰ cм^-3 та товщину підкладки ω_п = 200 мкм.

1. Невідомі коефіцієнти к₁ і к₂ можна знайти за умови, що результуюча концентрація домішки при х = х_е і х = х_к дорівнює нулю, тобто з ррозв’язку такої системи рівнянь:

;

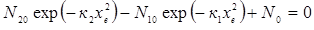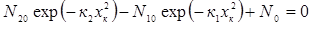
При заданих значеннях N_20, N_l0, N_0, х_е і х_к наведені рівняння являють собою систему нелінійних алгебраїчних рівнянь щодо невідомих к₁ і к_2. Ця система може бути розв’язана методом послідовних наближень.

Таблиця 2.3 – Електрофізичні та геометричні параметри структури транзистора

Параметр типу	Емітер п⁺- типу	База р-типу	Колектор n-типу
Поверхнева або вихідна концентрація домішки, см^-3	N₂₀ = 10²⁰	N₁₀ = 10¹⁸	N₀ = 10¹⁶
Середня концентрація домішки в шарі (або ОНЗ), см^-3	3,48 · 10¹⁹	4,79 · 10¹⁶	10¹⁶
Середня концентрація ННЗ, см^-3	5,63	4,09 · 10³ (БА)	1,96 · 10⁴
Середня рухливість ОНЗ, см²·В^-1·с^-1	72	234(БА) 49(БП)	1050
Середня рухливість ННЗ, см²·В^-1·с^-1	77,5	639(БА)	384
Середній коефіцієнт дифузії, см²·с^-1	2,0	16,5 (БА)	9,91
Час життя ННЗ, с	8,7·10^-9	15,8·10^-9	8,7·10^-9
Середня дифузійна довжина, см	1,32·10^-4	5,10·10^-4	2,94·10^-4
Середня питома провідність шару, Ом^-1·см^-1	401	1,79 (БА) 13,9 (БП)	1,68
Середній питомий опір шару, Ом·см	2,49·10^-3	0,558 (БА) 7,21·10^-2 (БП)	0,595
Питомий поверхневий опір шару, Ом/см²	13,8	5,58·10³(БА) 257(БП)	2380
Товщина шару, см	1,8·10^-4	1·10^-4	2,5·10^-4

Примітка. БА – база активна, БП – база пасивна.

Знайдемо перше наближення для коефіцієнта к_1. Концентрація N₂(x), як випливає з рис. 2.5, дуже швидко спадає зі зростанням х, тому N₂(х_к) << N_0, і прирівнявши до нуля два останні члени останнього рівняння, одержимо

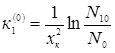
Підставивши числові значення величин, що входять у праву частину цього рівняння, отримаємо, що к₁⁽⁰⁾ = 0,79268·10⁸ см^-2. Тепер можна знайти наближене значення коефіцієнта к₂ за допомогою першого рівняння:

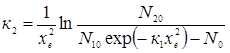
Значення коефіцієнта к₁ можна уточнити, визначивши к₁ з другого рівняння:

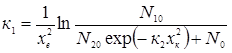
Розраховане за останньою формулою значення к₁ дозволяє уточнити значення к_2, знайдене раніше. Ітераційний процес закінчуємо, коли перші 4 – 5 знаків коефіцієнтів к₁ і к₂ перестануть змінюватися. Зазвичай для цього потрібно 5 – 7 ітерацій. Остаточно для даного прикладу маємо
к₁ = 0,790966 · 10⁸ см^-2
к₂ = 1,723686 · 10⁸ см^-2

Розподіл легуючих домішок в структурі N₂(x), N₂(x), N(x), розраховуємо за відповідними формулами. Результати обчислень наведені в табл. 2.4.

2. Власну концентрацію носіїв заряду в кремнії при Т = 300 К знаходимо з графіка (рис. 2.6)

Таблиця 2.4 – Розподіл домішок і рухливості носіїв заряду в заданій структурі

х, мкм	N₂(x), см_-3	N₁(x), см_-3	N(x), см_-3	N⁺(x), см_-3	μ_n, см^{2^/(В·с)}	μ_р, см²/(В·с)
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,2 3,4 3,6	1,00Е20 9,33Е19 7,59Е19 5,38Е19 3,32 Е19 1,78Е19 8,36 Е18 3,41Е18 1,21Е18 6,86Е17 3,75 Е17 1,98Е17 1,01Е17 4,99Е16 2,38Е16 1,09 Н16 4,88Е15 2,09Е15 8,70Е14 3,49Е14 1,35Е14 5,06 Е13 1,83Е13 2,16Е12 2,22ЕП 1,99Е10	5,00Е18 4,84Е18 4,41Е18 3,76Е18 3,01 Е18 2,27Е18 1,60Е18 1,06Е18 6,60Е17 5,08Е17 3,85Е17 2,88Е17 2,11E17 1,53 Е17 1,09Е17 7,62Е16 5,25Е16 3,56Е16 2,38Е16 1,56Е16 1,01Е16 6,46Е15 4,05 Е15 1,52 Е15 5,34Е14 1,77Е14	9,50Е19 8,85 Е19 7,15Е19 5,00Е19 3,02Е19 1,56Е19 6,76Е18 2,36Е18 5,62Е17 1,88Е17 2,20Е12 -7,92Е16 -1,00Е17 -9,28 Е16 -7,49Е16 - 5,5ЕТ -3,76 Е16 -2,36 Е16 -1,29Е16 -5,31Е15 0 3,59Е15 5,97 Е15 8,48 Е15 9,46Е15 9,82Е15	1,05Е20 9,82Е19 8,03Е19 5,75Е19 3,62Е19 2,01Е19 9,97 Е18 4,48Е18 1,88Е18 1,20 Е18 7,71Е17 4,96Е17 3,23 Е17 2,13Е17 1,42Е17 9,71Е16 6,74Е16 4,77Е16 3,47Е16 2,59Е16 2,03Е16 1,65Е16 1,41 Е16 1,15 Е16 1,05Е16 1,02 Е16	72 73 74 76 81 89 105 134 188 229 280 342 415 496 581 667 750 827 895 952 998 1032 1058 1087 1100 1105	49 50 50 51 52 54 57 65 79 91 106 125 148 -175 204 235 266 295 321 344 362 376 387 400 404 406

Примітка. Символом Е позначено основу 10 перед показником степеня, наприклад, 1,05Е20 означає 1,05·10²⁰.

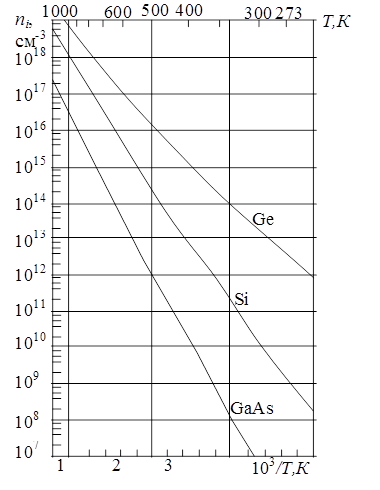
Рисунок 2.6 – Залежність власної концентрації носіїв заряду в германії, кремнії і арсеніді галію від температури

або розраховуємо за формулою:

n_i² (T) = BT³e^-ΔE/kT

де n_i = 1,4·10¹⁰ см^-3.

Рухливість електронів і дірок як функції координати розраховувалися за емпіричною формулою з використанням сумарної концентрації легуючої домішки N⁺(x).

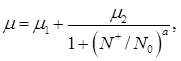
де N⁺ – сумарна концентрація розсіювальних центрів. Інші параметри наведені в табл. 2.5.

Таблиця 2.5 – Параметри напівпровідників для визначення рухливості носіїв заряду

Напівпровідник	μ_1, см²/В.с	μ_2, см²/В.с	N_0, см^-3	a
Кремній	65	Для електронів 1265	8,5·10¹⁶	0,72
Кремній	48	Для дірок 447	6,3·10¹⁶	0,76
Германій	50	Для електронів 3850	8,1·10¹⁶	0,48
Германій	42	Для дірок 1860	1,4·10¹⁶	0,43

Результати розрахунку наведені на рис. 2.7.

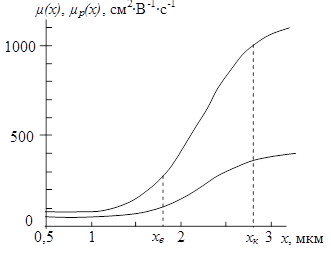
Рисунок 2.7 – Залежність рухливості електронів і дірок від координати в активній області структури транзистора

Середні значення рухливостей основних і неосновних носіїв заряду в шарах активної області структури визначалися як середні арифметичні значення від рухливостей на кордонах кожного шару і наведені в табл. 2.6. Наприклад, середні значення рухливостей електронів і дірок в активній базі визначалися як

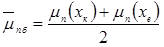
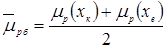
Таблиця 2.6 – Електрофізичні та геометричні параметри р-n-переходів

Параметр	Емітерний р-n-перехід	Колекторний р-n-перехід
Градієнт концентрації домішки а, см^-4	1,23·10²²	4,34·10²⁰
Контактна різниця потенціалів φ_к, В	0,829	0,709
Розширення ОПЗ в область бази при U = 0, лінійна апроксимація, см	0,0875·10^-4	0,253·10^-4
Ширина ОПЗ при U = 0, см	0,175·10^-4	0,507·10^-4
Глибина р-n переходу, см	1,8·10^-4	2,8 ·10^-4
Довжина l, см	10·10^-4	70·10^-4
Ширина z, см	50·10^-4	70·10^-4
Периметр П, см	1,2·10^-2	2,8·10^-2
Площа плоскої частини, см²	5·10^-6	49·10^-6
Площа бічної частини, см²	3,39·10^-6	12,3·10^-6
Повна площа А, см²	8,39·10^-6	61,3·10^-6
Щільність зворотного струму насичення, А/см²	0,9·10^-10	1,46·10^-10
Зворотний струм насичення, А	0,756·10^-15	8,95·10^-15
Бар'єрна ємність у режимі I_e= 1 мА, U_к = - 5 В, пФ	0,990	0,556

Середнє значення коефіцієнта дифузії визначалося зі співвідношення Ейнштейна з використанням середньої рухливості неосновних носіїв заряду в кожному шарі. Середнє значення дифузійної довжини розраховувалося за формулою

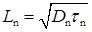Середні значення концентрації основних носіїв заряду вважалися такими, що дорівнювали середнім значенням результуючої концентрації домішки в кожному шарі. Середнє значення концентрації основних носіїв заряду в емітері

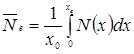З урахуванням профілю дифузійного розподілу домішки в активній області структури транзистора інтегрування останнього виразу дозволяє записати

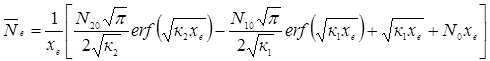Таблиця значень функції помилок (erf-функції) наведена в додатку В. Ці значення можна розрахувати і за допомогою наближеного виразу

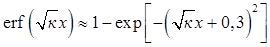Середня концентрація домішки в активній і пасивній областях бази розрізняються (див. табл. 2.3). Середня концентрація домішки в пасивній області бази розраховується за формулою

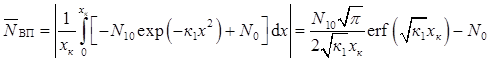Середня концентрація домішки в активній області бази

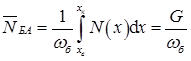У цій формулі величина G називається числом Гуммеля і визначається виразом

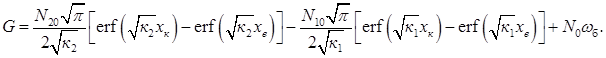Вважаємо, що в колекторі середнє значення концентрації домішки дорівнює N_0.

Середня питома провідність і питомий опір кожного шару розраховані за формулами

;

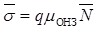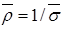де µ_ОНЗ – середнє значення рухливості основних носіїв заряду в даному шарі.

Питомий поверхневий опір (опір шару) розраховувався як відношення середнього питомого опору до товщини шару. Наприклад, в активній базі

ρ_SБА = ρ_БА /ω_бт = 0,558/10^-4 = 5,58∙10³ Ом/□ = 5,58 кОм/□,

у пасивній базі

ρ_SБП =ρ_БП /х_к = 7,21 ∙ 10^-2/2,8∙10^-4 = 257 Ом/□.

Слід зазначити, що розрахунок питомого опору ρ_SБА за незалежно усередненими значеннями рухливості і концентрації основних носіїв заряду дає значення ρ_SБА з похибкою приблизно 20%, однак при оцінних розрахунках така помилка допустима. Результати розрахунку середніх значень електрофізичних параметрів транзистора зведені в табл. 2.3.

У транзисторі, отриманому методом дифузії домішки, розрахунок ширини ОПЗ емітерного і колекторного р-n-переходів є складною задачею і в загальному випадку потребує залучення числових методів. Проте в кожному конкретному випадку можна знайти вдалі апроксимації, які дозволяють оцінити ширину ОПЗ колекторного і емітерного р-n-переходів.

Розподіл домішки в активній області структури, побудований за даними табл. 2.4, наведено на рис. 2.8.

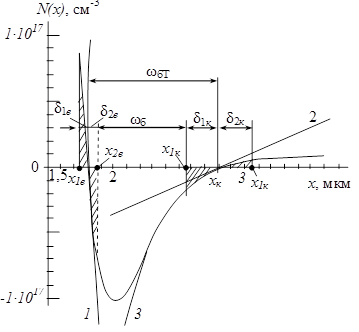
Рисунок 2.8 – Залежність концентрації легуючої домішки від координати в активній області структури транзистора

Для оцінювання ширини ОПЗ і контактної різниці потенціалів реальний розподіл домішки у районі координат х_е і х_к можна замінити лінійним (криві 1 і 2). Вираз для градієнта концентрації домішки отримаємо, диференціюючи дифузійний розподіл домішки в активній області за х:

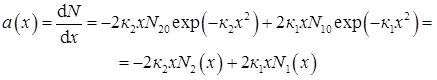
Розраховані за цією формулою значення градієнтів концентрації домішки в емітерному a_e = |a (x_e)| і колекторному a_к = |a (x_к)| р-n-переходах наведені в табл. 2.6. Там же подані значення контактної різниці потенціалів емітерного і колекторного переходів, розраховані за формулою

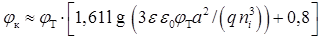де φ_т = 0,026 В;
q = 1,6 · 10^-19 Кл.
і значення рівноважної ширини ОПЗ цих переходів, розраховані за формулою

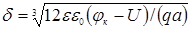
у припущенні лінійної апроксимації розподілу домішки. Враховуючи, що на емітерний р-n-перехід в активному режимі подано пряму напругу і ширина ОПЗ цього переходу менша за рівноважну, апроксимація розподілу домішки лінійною залежністю дає невелику похибку при розрахунках.

Апроксимація розподілу домішки в колекторному р-n-переході лінійною залежністю (крива 2), як випливає з рис. 2.8, є більш грубим наближенням при розрахунках розширення ОПЗ.

Для уточненого розрахунку ширини ОПЗ колектора замінимо реальний розподіл домішки N₁(x) деяким експоненціальним розподілом

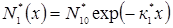Будемо вважати, що апроксимуюча крива N^*₁(х) збігається з кривою N₁(х) в точках з координатами х_е і х_к. Ця умова дозволяє визначити

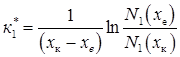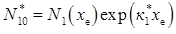Розрахунок з використанням значень N₁(х_е) = -3,85·10¹⁷ см^-3 і N₁(х_к) = 1,01·10¹⁶ см^-3 за табл. 2.4 дозволяє визначити к^*₁ = 3,64·10⁴ см^-1; N₁₀^* = 2,7·10²⁰ см^-3. Таким чином, ми замінили реальний розподіл домішки N(х), визначений раніше, в районі колекторного переходу наближеним експоненціальним розподілом

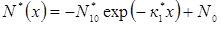Цей розподіл домішок нанесено на рис. 2.8 штриховою лінією (крива 3) і досить близький до реального розподілу домішки.

Для р-n-переходу з експоненціальним розподілом домішки теорія дає таке трансцендентне рівняння, що пов'язує в неявному вигляді повну ширину ОПЗ р-n-переходу δ з прикладеною напругою U:

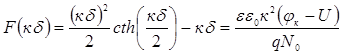. (2.1)

При малих кδ < 2 функція F(кδ) ≈ (кδ)³ / 12. Якщо позначити праву частину рівняння через B = εε₀κ²(φ_κ -U )/(qN₀), то можна визначити

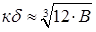. (2.2)

Це розв’язання відповідає апроксимації експоненціального розподілу домішок поблизу точки х до лінійної залежності і дає похибку менше 5% при В < 0,6. При великих κδ > 4 cth (κδ /2) ≈ 1, і тому
F (κδ) ≈ (κδ)² /2 - κδ = B. (2.3)

Розв’язання отриманого квадратного алгебраїчного рівняння щодо κδ дає

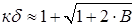. (2.4)

При В > 100 величина 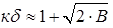з похибкою не більше 7%, що відповідає апроксимації розподілу домішки в р-n-переході ступінчастою залежністю. У діапазоні 0,6 < В < 100 р-n-перехід є плавним і найкращі результати виходять при розрахунку значень κδ за допомогою модифікованого виразу

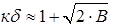. (2.5)

Цей вираз при В > 0,6 дає похибку не більше 5%, Графік залежності F (κδ) відповідно до виразу для F (κδ) і апроксимації цієї залежності наведені на рис. 2.9.

Для колекторного р-n-переходу величина к, що входить в рівняння (2.1), дорівнює κ^*_1, а величина δ визначає ширину ОПЗ колектора δ_κ. За заданим значенням U можна за допомогою графіка, зображеного на рис. 2.9, або за формулами (2.2) – (2.5) визначити добуток κδ_κ, а потім знайти δ_κ.

Наприклад, для колекторного р-n-переходу при U = 0 права частина рівняння (2.1)

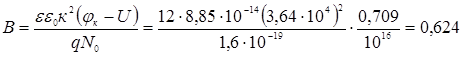
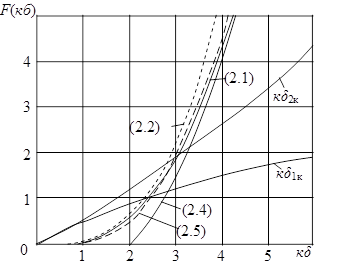
Рисунок 2.9 – Номограма для розрахунку розширення ОПЗ-колектора р-n-переходу

З графіка рис. 2.9 знаходимо відповідне значення κ₁^*δ_κ = 2κ і розраховуємо δ_κ = 2/ κ₁^* = 2/ 3,64·10⁴ = 0,539·10^-4 см = 0,549 мкм. Це значення дещо більше від значення 0,507 мкм, отриманого при заміні розподілу домішки лінійним. Розширення ОПЗ колектора в область р-бази δ_1κ і в область n-колектора δ_2κ пов'язані з повною шириною ОПЗ співвідношеннями:

;
.

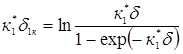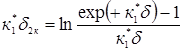Значення δ_1κ δ_2κ можна розрахувати за наведеними формулами або визначити з графіка (рис. 2.9): κ₁^*δ_1κ = 0,84 ; κ₂^*δ_2κ = 1,16, звідки δ_1κ = 0,23 мкм; δ_2κ = 0,32 мкм. Визначені за даною методикою значення δ_1κ, δ_2κ і δ_κ як функції зворотної напруги зміщення колекторного переходу наведено в табл. 2.7.

Таблиця 2.7 – Дані до розрахунку розширення ОПЗ колектора

U_К, B	B	κδ_κ	δ_κ, мкм	δ_1κ, мкм	δ_2κ, мкм
0 -1 -2 -4 -5 -6 -8 -10 -20 -30 -40 -50 -60	0,62 1,50 2,38 4,14 5,02 5,90 7,66 9,42 18,2 27,0 35,8 44,6 53,4	2,02 2,81 3,25 3,95 4,25 4,50 5,04 5,46 7,12 8,42 9,52 10,5 11,4	0,549 0,769 0,892 1,08 1,17 1,24 1,38 1,50 1,95 2,31 2,61 2,88 3,13	0,230 0,302 0,335 0,385 0,393 0,412 0,450 0,467 0,539 0,585 0,619 0,646 0,668	0,320 0,467 0,558 0,701 0,755 0,810 0,334 1,03 1,42 1,73 1,99 2,24 2,46

Емітерний р-n-перехід складається з плоскої частини, розміри якої збігаються з розмірами вікна в плівці оксиду, створеного методом фотолітографії для дифузії емітерної домішки і бічних частин, пов'язаних з бічною дифузією домішки. Будемо вважати, що бічна поверхня р-n-переходу являє собою частину циліндричної поверхні з радіусом, що дорівнює глибині залягання р-n-переходу. Геометричні розміри р-n-переходів наведені в табл. 2.6.

Площа плоскої частини емітера
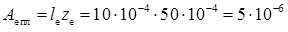см².

Площа бічної частини емітера
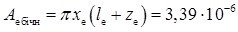см².

Повна площа емітера
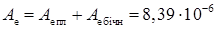см².

Аналогічно розраховується площа колекторного р-n-переходу. Результати розрахунку зведені в табл. 2.6.

3. Для проведення розрахунків коефіцієнтів передачі струму необхідно визначити ширину квазіелектронейтральної бази з урахуванням розширення ОПЗ р-n-переходів. Розширення ОПЗ колектора в базу при U_κ = -5 В (робочий режим) наведено в табл. 2.7 і складає δ_1κ = 0,393 мкм. Розрахунок розширення ОПЗ емітера в базу δ_2e ускладнений тією обставиною, що пряма напруга на емітері невідома. У робочому режимі в колі емітера заданий прямий струм І_Е = 1 мА. Напругу на емітері можна обчислити за формулою

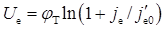Номінальна густина струму емітера

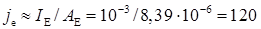А/см².

Величина j^'_e₀ поки невідома, але її можна оцінити, враховуючи, що зворотний струм емітера визначається в основному електронною складовою, яку можна розрахувати за відповідною формулою з урахуванням даних табл. 2.3:

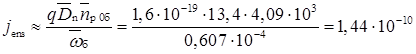А/см².

На відміну від даного в табл. 2.3, значення коефіцієнта дифузії усереднено в діапазоні х від 1,8 до 2,407 мкм. Остаточно за останньою формулою знаходимо U_е = 0,710 В, вважаючи j^'_eo ≈ j^'_ens.

Розширення ОПЗ емітера в область бази
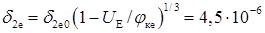см = 4,5 · 10^-2 мкм.

Методика розрахунку коефіцієнта переносу складається з двох етапів. На першому етапі за допомогою числового інтегрування знаходимо розподіл концентрації неосновних носіїв заряду в квазінейтральній базі в межах від х_2е= 1,845 мкм до х_1к = 2,407 мкм

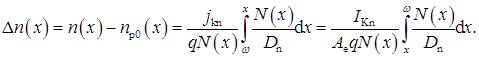
Обчислення інтеграла показано в табл. 2.8.

Розділимо інтервал інтегрування на 10 частин. Інтегрування зручно вести за методом трапецій, обчислюючи значення інтеграла за формулою
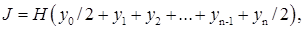(2.6)
де Н - крок інтегрування, який в даному випадку дорівнює 0,0562 мкм;
у₀ і у_n - початкове і кінцеве значення функції.

Таблиця 2.8 – До розрахунку інтеграла (2.6)

Номер кроку	х, мкм	N(x), см^-3	N⁺(x), см^-3	D_n(x), см²/с	N⁺(x)/D_n(x), см^-5/с	Δn(x), см^-3
0 1 2 3 4 5 6 7 8 9 10	2,4070 2,3508 2,2946 2,2384 2,1822 2,1260 2,0698 2,0136 1,9574 1,9012 1,845	-3,654Е16 -4,589Е16 -5,55Е16 -6,727Е16 -7,841Е16 -8,872Е16 -9,670Е16 -10,016Е16 -9,598Е16 -7,975Е16 -4,556Е16	6,574Е16 8,048Е16 9,772Е16 1,227Е17 1,528Е17 1,914 Е17 2,408Е17 3,045Е17 3,869Е17 4,935Е17 6,315Е17	19,5 18,3 17,2 15,8 14,6 13,4 12,1 11,0 9,88 8,85 7,91	1,873Е15 2,505Е15 3,231Е15 4,244Е15 5,370Е15 6,642Е15 7,959Е15 9,U7E15 9,712Е15 9,008Е15 5,760Е15	0 1,675Е15 3,199Е15 4,592Е15 6,093Е15 7,762Е15 9,774Е15 1,243Е16 1,641Е16 2,338Е16 4,749Е16

Інтегрування можна вести за методом трапецій, але більшу точність дає метод парабол (метод Сімпсона), відповідно до якого

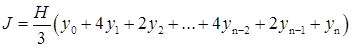На цій стадії можна уточнити значення струму j_ens.

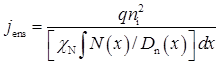
За методом парабол обчислимо 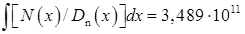см^-5·с.
Остаточно i>j_ens = 0,899·10^-10 А/см². В даному випадку метод трапецій дає помилку менше 3%. При розрахунку Δn(x) задавалося значення j_nк = 10³ А/см².

На другому етапі за обчисленою залежністю Δn(x) знаходимо значення струму об'ємної рекомбінації електронів в базі на основі формули

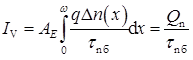Обчислення за методом трапецій дає 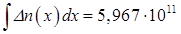см^-2, а за методом парабол – 5,99·10¹¹ см^-2.

Відповідно до даної формули

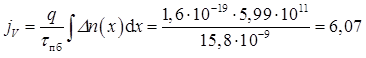А/см².

Знайдемо коефіцієнт переносу для нормального режиму

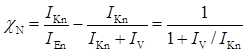
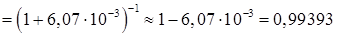Якщо коефіцієнт інжекції дорівнював би одиниці, то коефіцієнт передачі струму бази дорівнював би .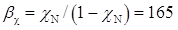

Обчислення коефіцієнта інжекції y_N це складна задача, розв’язання якої в загальному випадку потребує застосування числових методів. У даному розрахунку розглянемо метод оцінення, що дозволяє оцінити y_N. Почнемо з попереднього розрахунку струму дірок j_ер, інжектованих в квазіелектронейтральну область n⁺-емітера. Дірки, інжектовані в емітер, попадають в сильне гальмівне електричне поле, обумовлене нерівномірним розподілом донорів в емітері. Напруженість цього поля на лівій границі ОПЗ емітера при x = х_1е = 1,8 – 0,045 = 1,755 мкм визначається виразом

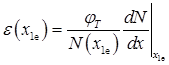Значення N(x_1е) = 7,63·10¹⁶ см^-3 обчислюємо за формулою з визначення профілю дифузійного розподілу домішок. Значення при x = x_1е обчислюємо за формулою для градієнта концентрації домішки: а_е = -1,85·10²² см^-4. Звідси, напруженість поля ε (x_1е) = 6,25·10³ В/см.

Таким чином, дірки в емітері дифундують проти електричного поля. Як відомо з фізики напівпровідників, в цьому випадку для опису розподілу дірок від координати слід користуватися не дифузійною довжиною, а довжиною затягування або дифузійною довжиною проти поля

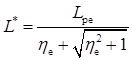У цій формулі величина 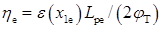називається фактором поля. Вважаючи, що μ_ре = 100 см²·В^-1·с^-1 (див. рис. 2.7), 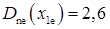см²·с^-1; L_pе = 1,5 мкм обчислюємо η_е = 18,2; L^* = 4,13·10^-6 см = 4,13·10^-2 мкм.

Дірковий струм емітера на границі ОПЗ

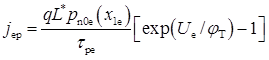Передекспоненційний множник визначає густину діркового струму насичення емітера. Враховуючи, що 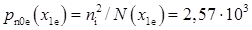см^-3, можна розрахувати

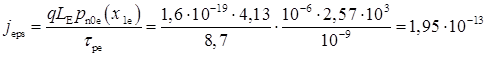А/см².

При оцінюванні значення струму j_еps вважалося, що дифузія дірок проти поля відбувається в постійному електричному полі напруженістю, яка дорівнює ε (х_1е). Реально напруженість гальмівного електричного поля спадає практично лінійно до поверхні кристала. Тому в середньому вплив поля ε (х_1е) слабкіший і значення струмів j_еs та j_еps дещо більше. Однак, зберігаючи отримані оцінні значення, знайдемо коефіцієнт інжекції за формулою

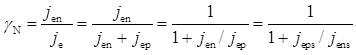Використовуючи отримане раніше значення j_еns = 0,899·10^-10 А/см², отримуємо 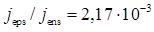і величину .

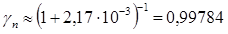Якби коефіцієнт Χ_N дорівнював би одиниці, то коефіцієнт передачі струму бази дорівнював би 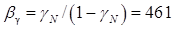. З урахуванням раніше обчисленого значення Χ_N величин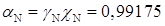а , а .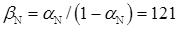

Таким чином, у даному випадку коефіцієнт передачі струму бази β_N більшою мірою визначається значенням коефіцієнта переносу. При більшому, ніж в даному прикладі, часі життя електронів у базі коефіцієнт β_N більшою мірою буде визначатися коефіцієнтом інжекції ϒ_N.

Складові щільності струму насичення емітерного р-n-переходу розраховані раніше. Повна густина струму насичення емітера

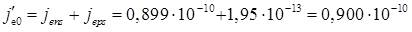А/см².

З урахуванням повної площі емітера знайдемо струм насичення емітера

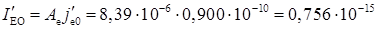А/см².

Як і в транзисторі з однорідною базою, складова струму насичення колектора, обумовлена термогенерацією неосновних носіїв заряду (електронів) у базі, 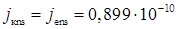А/см².

Діркова складова струму насичення, обумовлена термогенерацією дірок в квазіелектронейтральному колекторі, визначається тією ж формулою, якщо в ній замінити індекс n на р і навпаки. Тоді густину струму j_крs можна розрахувати за формулою

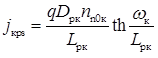Вважаючи, що початкова ширина n-області колектора ω_кт = 2,5 мкм (табл. 2.3) і в робочому режимі при U_к = - 5 В &delta_2к = 0,755 мкм (табл. 2.7), отримуємо ширину квазіелектронейтральної області колектора: 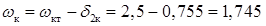мкм. Відповідно до даних табл. 2.3 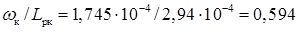. При цьому значенні аргументу відповідно до таблиці додатка В маємо th 0,594 ≈ 0,531.

На підставі цих даних отримуємо

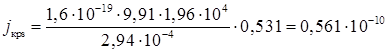А/см².

Густина струму насичення колектора

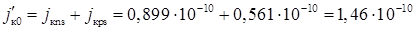А/см².

Струм насичення колектора з урахуванням повної площі колектора (див. табл. 2.6).

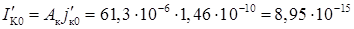А/см².

Опір активної області бази розрахуємо використовуючи дані табл. 2.3:

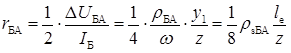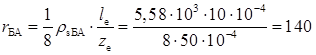Ом.

Опір пасивної області бази

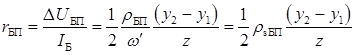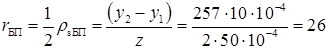Ом.

Опір розтікання базового контакту розрахуємо за формулою

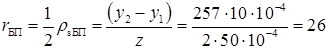Приймемо

ρ_с = 3,0·10^-5 Ом·см²; у_м = у₃ – у₂ = 10 мкм.

Аргумент гіперболічного котангенса

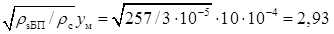відповідно cth 2,93 ≈ 1 і опір

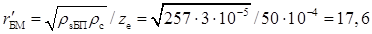Ом.

контактний опір 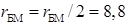Ом.

Опір бази транзистора

r_Б = r_БА + r_БП + r_БМ ≈ 140 + 26 + 9 = 175 Ом.

Опір тіла колектора має дві складові, перша з яких визначається напругою на опорі високоомного шару колектора n-типу електропровідності, а друга – напругою на опорі низкоомної підкладки n⁺-типу з концентрацією домішки N_n = 10²⁰ см^-3, питомим опором ρ_n = 0,88·10^-3 Ом·см і товщиною ω_n = 200 мкм. Перша складова

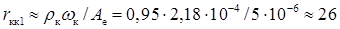Ом.

Товщина квазіелектронейтрального n-колектора розраховувалася при U_к = 0 з урахуванням даних табл. 2.7. При цьому δ_2к = 0,32 мкм і ω_к = ω_кт - δ_2к = 2,5 - 0,32 = 2,18 мкм.

Друга складова

r_кк2 ≈ ρ_nω_n/А_е = 0,88·10^-3 · 200·10^-4 / 5·10^-6 ≈ 3,5 Ом.

Результуючий опір тіла колектора

r_кк = r_кк1 + r_кк2 = 26 + 3,5 =29,5 Ом.

Розрахуємо питому бар'єрну ємність емітера при U_е = 0 (ширина ОПЗ дана в табл. 2.6)

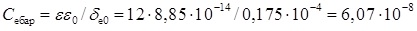см².

Бар'єрна ємність емітера при U_е = 0

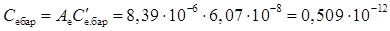Ф = 0,509 пФ.

У робочому режимі при І_е = 1 мА маємо U_е = 0,71 В, δ_в = 0,09 мкм і бар'єрна ємність емітера С_е бар = 0,9·10^-12 Ф = 0,99 пФ.

Питому і повну бар'єрну ємність колектора розраховуємо при U_к = - 5 В (при цьому δ_к = 1,17 мкм, як випливає з табл. 2.7):

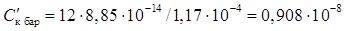Ф/см²;

С_{к бар} = А_к · С^'_{к бар} = 61,3·10^-6·0,908·10^-8 = 0,556·10^-12 Ф = 0,556 пФ.

4. Розрахуємо параметри Т-подібної еквівалентної схеми для малого сигналу в робочій точці. Диференціальний опір емітера r при I_е = 1 мА становить 25,8 Ом

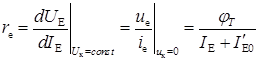Розрахуємо першу складову диференціальної вихідної провідності g^'_к в робочій точці I_е = 1 мА; U_к = - 5 В. Оскільки величина α_N і ширина ОПЗ визначалися числовими методами, розрахунок g^'_к треба вести з використанням такої формули

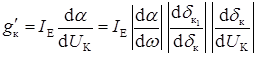Проведений раніше розрахунок показав, що при I_е = 1 мА; U_к = - 5 В величина Χ_N = 1 - 6,07·10^-3; ϒ_N = 1 - 2.17·10^-3; α_N = 1 - 8,24·10^-3; β_N = 121,4 (така форма запису краща для збереження точності значення параметрів). За вже наведеною числовою методикою треба повторити всі розрахунки при зміні напруги на колекторі, наприклад, на 1 В. Задаючи U_к = - 6 В, отримуємо: Χ_N = 1 - 5,88·10^-3; ϒ_N = 1 - 2,15·10^-3; α_N = 1 - 8,03·10^-3; β_N = 124,5.

Остаточно отримуємо

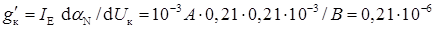Ом^-1.

Якби ця складова була єдина, то диференціальний опір колектора бази дорівнював би r_κ = 1/ g^'_κ = 4,76 МОм.

Для визначення другої складової провідності колектора g^"_κ необхідно розрахувати струм генерації носіїв в ОПЗ колектора, який визначається такою формулою:

;

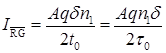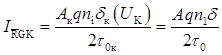де τ_0к = 7,26·10^-8 с – генераційний час життя носіїв заряду в р-n переході.

Скориставшись даними табл. 2.7 при U_к = - 5 В, отримаємо δ_к = 1,17 мкм; I_RGK = 1,106·10^-10 А, а при U_к = - 6 В отримаємо δ_к = 1,24 мкм; I_RGK = 1,172·10^-10 А.

На підставі цих даних обчислюємо

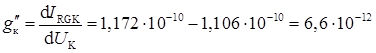Ом^-l.

Таким чином, g^'_κ << g^"_κ, і тому диференціальний опір колектора r_к = 4,76 МОм.

Розраховуємо коефіцієнт зворотного зв'язку за напругою. Відповідно до граничних умов для концентрації неосновних носіїв

;

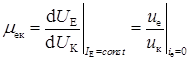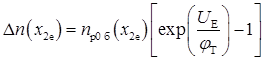Знайдемо з цього виразу напругу

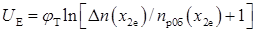
Задамо напругу на колекторі U_к = - 5 В. При цьому з табл. 2.8 маємо Δn_e1 = Δn(x_2e) = 4,749·10¹⁶ см^-3 при х_e = 1,845 мкм. Збільшимо зворотну напругу колектора на 1 В до U_к = 6 В. Проводячи обчислення Δn(х) за викладеною раніше методикою, отримуємо Δn_e1 = Δn(x_2e) = 4,749·10¹⁶ см^-3. Нехтуючи у формулі одиницею, знаходимо

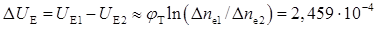В.

Оскільки зміна напруги ΔU_к складає 1 В, то

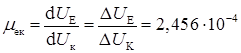Опір бази та коефіцієнти передачі струму бази розраховані раніше.

5. Спочатку оцінимо напругу пробою колекторного переходу, аппроксимуючи розподіл домішок у ньому лінійним законом з градієнтом а_к = 4,34·10²⁰ см^-4. Розрахунок за формулою

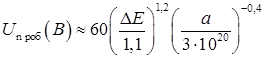дає U_{К проб} ≈ 52 В. Це груба оцінка. Номограми, основані на точних розрахунках напруги лавинного пробою, наведені в книзі І. В. Грехова, Ю. Н. Сережкина. «Лавинный пробой р-п перехода в полупроводниках» (Ленинград: Енергия, 1980, С. 62), З цими номограмами можна уточнити значення U_{К проб} ≈ 65 В.

Напругу лавинного пробою емітерного р-п-переходу можна також оцінити за цією ж формулою. Оцінювання дає U_{Е проб} = 14 В.

Дані табл. 2.7 показують, що напруга змикання U_зм значно перевищує напругу лавинного пробою колектора.

Пробивну напругу колектора транзистора зі спільним емітером при нульовому струмі бази можна оцінити за формулою

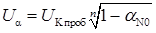вважаючи n = 3, β_N0 = 121 [β_N = α_N / (1 - α_N)] і U_{К проб} = 65 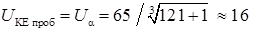В:

В.

Треба зазначити, що отримане значення годиться тільки як дуже груба оцінка.

Будемо вважати, що для кремнієвого транзистора максимальна температура переходу Т_{j max} = 150 °C. Тепловий опір перехід – корпус, враховуючи малі розміри емітера і бічне розтікання тепла, можна оцінити за формулою

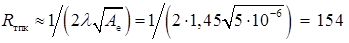К / Вт.

Вибираємо корпус з тепловим опором R_тк-с = 300 К / Вт. Тоді повний тепловий опір R_тп-с = R_тп-к + R_тк-с = 454 °С/Вт. При температурі навколишнього середовища Т₀ = 25 °С максимальна потужність, що розсіюється колектором,

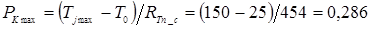Вт.