ЛАБОРАТОРНА РОБОТА № 2

КОНСТРУКТИВНИЙ РОЗРАХУНОК БІПОЛЯРНИХ

ТРАНЗИСТОРІВ

 

 

Мета роботи: провести конструктивний розрахунок біполярного транзистора, використовуючи вихідні дані.

 

Теоретичні відомості

 

Вибір геометричних розмірів транзистора, кількість емітерів, базових і колекторних контактів та їх форма визначаються вимогами до параметрів. Максимальна густина емітерного струму, перевищення якого призводить до зменшення коефіцієнта підсилення транзистора, обмежує робочий струм. Визначення розмірів емітерної області, а отже й топології транзистора проводиться, виходячи із забезпечення максимального коефіцієнта підсилення при робочому струмі емітера [1].

Розрахункові співвідношення для визначення геометричних розмірів емітерної  області.

 Модуляція провідності базової області транзистора приводить до зміни коефіцієнта передачі й опору базової області. Ступінь модуляції провідності залежить від рівня інжекції:

 

 ,                         (2.1)

 

                                                                                                          

де  й  – концентрація неосновних і рівноважна концентрація основних носіїв на границі збідненого шару емітерного переходу в базовій області [1].

Коефіцієнт підсилення струму

 

                                                (2.2)

 

досягає максимального значення при

 

.                                                     (2.3)

 

Якщо  (високий рівень інжекції),  зменшується. Виконання умови (2.3) при максимальному робочому емітерному струмі  забезпечує роботу схеми при максимальному значенні .

Настання високого рівня інжекції відбувається або по всій частині  дна емітерного переходу, або ініціюється струмом , який протікає через базову область (рис. 2.1), що й створює додатковий зсув на емітерному переході (поверхня емітерного переходу перестає бути еквіпотенціальною).

 

 

 

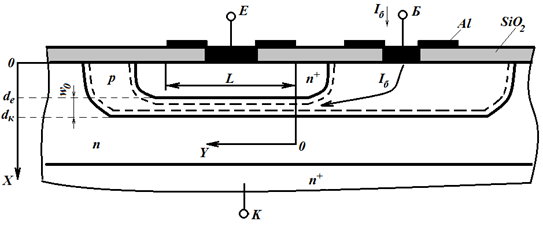
Рисунок 2.1 – Структура дискретного біполярного n-p-n-транзистора

 

Останнє викликає зміну густини емітерного струму в дні частини емітера, тобто залежність (див. рис. 2.2).

 

 

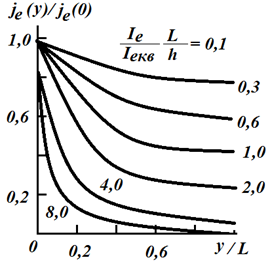
Рисунок 2.2 – Залежності відношення  від структурних

 параметрів транзистора

 

Це явище називається ефектом відтискування емітерного струму. Максимальна густина струму при, а мінімальна — при . Цей ефект буде істотним, якщо

,                                                 (2.4)

                                                                                                                                        

де ‒ опір базової області:

 ,                                     (2.5)

 

де  ‒ ширина дна частини емітерних областей (у напрямку, перпендикулярному до площини на рис. 2.1) [1].

З урахуванням умов (2.3) і (2.4) вирази для визначення максимального питомого струму (на одиницю ширини  емітера) мають вигляд

 

 

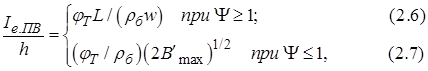
де ‒ величина емітерного струму, перевищення якого викликає перехід до високого рівня інжекції;

 ‒ максимальне значення коефіцієнта підсилення струму (якщо  значення ), при якому виконується умова (2.3)

 

 .                           (2.8)     

 При  спад  зі збільшенням емітерного струму відбувається через перехід до високого рівня інжекції, викликаного дією ефекту відтискування, а при — перехід до високого рівня інжекції без дії ефекту відтискування. Як видно з рис. 2.1 і 2.2, при  робочою або «активною» є права частина емітера, найближча до базового контакту [1 – 4].

На рис. 2.3 подана залежність від , відповідно до умови . Область, що перебуває вище кривої, визначає дію рівняння (2.6), а нижче ‒ (2.7). Для визначення розмірів емітерної області за допомогою співвідношень (2.6) ‒ (2.8) при обраних параметрах дифузійного процесу й напівпровідникової пластини необхідно знайти .

 

 

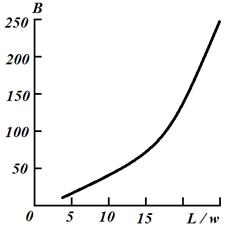
Рисунок 2.3 ‒ Крива, що визначає механізм настання високого

 рівня інжекції

 

Залежність коефіцієнта підсилення від струму  (або ) у робочій області має складну аналітичну форму. Її можна апроксимувати такою залежністю:

,                             (2.9)

 

де ,,  ‒ сталі, зазвичай визначені з експериментальних даних. Максимальне значення відповідає .  Якщо допустима величина  при максимальному робочому струмі, тобто можливо , то можна використовувати менші розміри емітерних областей. Відповідне оцінення зменшення В може бути зроблено за допомогою (2.9).

Геометрія транзисторів. При виборі геометрії транзистора необхідно враховувати як електричні характеристики розроблюваного приладу, так і характеристики технологічного процесу й допуски на геометричні розміри. Зазвичай в інтегральних транзисторів  (2.7), тобто високий рівень інжекції настає через дію ефекту відтискування емітерного струму.

Для малопотужних транзисторів ( мА) з високою швидкодією необхідно мінімізувати їхні геометричні розміри з метою зменшення ємностей емітерного, колекторного й ізолювального переходів. Ці транзистори зазвичай мають структуру, показану на рис. 2.4 [1].

 

 

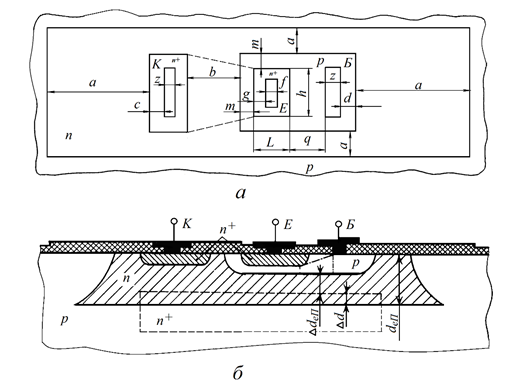
Рисунок 2.4 – Топологія (а) і структура (б) інтегрального біполярного транзистора

 

Довжина емітера вибирається мінімальною для зменшення впливу ефекту відтискування емітерного струму. Транзистори з колекторними струмами до 10 мА зазвичай мають структуру із двома базовими контактами, показану на   рис. 2.5.

У цьому випадку при використанні співвідношень  (2.6) ‒ (2.8)  в (2.8) величина  замінюється на , оскільки «активними» є обидві сторони емітера, що перебувають поблизу базових контактів. Тому, на відміну від структури з одним базовим контактом, у розглянутому транзисторі () значення   буде у два рази меншим (при однакових ), тобто буде у два рази меншою площа емітера. У потужних транзисторах ( ‒ десятки міліамперів) для мінімізації займаної ними площі особливе значення має одержання максимального відношення «активної» частини периметра емітерів до площі емітерів. Тому потужні транзистори мають смушкову структуру, що складається з декількох емітерів і базових контактів, з'єднаних паралельно (рис. 2.6) [1, 5,6].

 

 

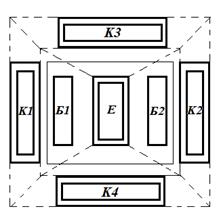
Рисунок 2.5 – Топологія n-p-n-транзистора зі зменшеними опорами базової області та тіла колектора

 

В емітерах, що мають більшу ширину , необхідно оцінити спад напруги на його контактній площадці. Він не повинен перевищувати  (2.4), тому що в іншому випадку периферійні ділянки емітера будуть інжектувати менший струм, ніж ділянки, найближчі до зовнішньої частини електрода. Це погіршує електричні характеристики транзистора (зменшення, ). Тому іноді буває доцільною розбивка емітера на частини, як показано на рис. 2.6.

 

 

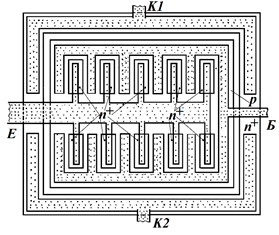
Рисунок 2.6 –  Топологія потужного біполярного n-p-n-транзистора

 

Опір базової області. При розрахунках опору базової області структуру розбивають на області, опір яких легко визначається. Однак, на відміну від опору,   залежить від емітерного струму або від рівня інжекції. Останній модулює провідність частини базової області, що перебуває під основою емітера . Рівняння для визначення опору цієї ділянки базової області транзистора з конфігурацією, показаною на рис. 2.2, залежно від емітерного струму має вигляд [1 – 6]:

 

,

 

 

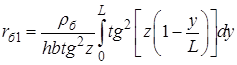де  й деякий еквівалентний струм .

Зробивши інтегрування, одержимо

 

                       (2.10)

 

де  – опір базової області під частиною дна емітера.        При, тобто при  струмі, вираз (2.10) має вигляд:

 

.                                                     (2.11)

                                                                               

З порівняння (2.5) і (2.11) видно, що, як і слід було сподіватися, вирази для визначення опору областей збігаються.

На рис. 2.7 показано залежність нормованого опору  від структурних і електричних характеристик. При заданих параметрах транзисторної структури за допомогою цієї залежності можна визначити опір частини базової області   .

Облік опору периферійних ділянок базової області ( ) за допомогою співвідношень (2.4), (2.5)  дозволяє  знайти . Для структури транзистора із двома базовими контактами співвідношення (2.10) запишемо як:

.                                     (2.12)

 

Як видно з рис. 2.5, 2.6 і виразів (2.10), (2.12) використання транзистора із двома базовими контактами дозволяє в 2 ÷ 4 рази зменшити  порівняно з опором у структурі з одним базовим контактом. Для зменшення  в деяких випадках використовують Г-подібний контакт до базової області, що охоплює одну з торцевих частин емітера, або П-подібний.

 

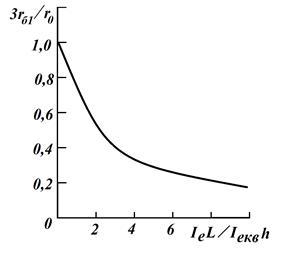
Рисунок 2.7 – Залежність нормованого опору базової області

n-p-n-транзистора від параметрів транзисторної структури

 

Розрахунок  коефіцієнта передачі n-p-n-транзистора.

Статичний коефіцієнт передачі емітерного струму  й коефіцієнта підсилення  є одними з основних параметрів транзистора. Вони визначають не тільки схемні, але й структурні особливості транзистора. Коефіцієнт

,                                                     (2.13)

 

де  – коефіцієнт інжекції емітерного p-n-переходу;

 –  коефіцієнт переносу.

Зазвичай

  % /^оС.

 

Статичний коефіцієнт передачі при нормальному включенні.

Коефіцієнт переносу визначається відомим співвідношенням

 

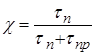,                                             (2.14)

 

де  – середній час життя неосновних носіїв у базовій області;

– час пролітання носіїв через останню. З врахуванням  вираз (2.14) перетвориться на:

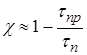.                                            (2.15)

Величина  визначається з (2.13). Вираз для визначення коефіцієнта інжекції запишеться у вигляді 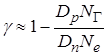[1 – 6]:

 

,                                              (2.16)

 

де  – середній коефіцієнт дифузії дірок в емітері;

 – питома кількість донорної домішки в емітері. У виразі (2.16) з урахуванням ефектів, пов'язаних із сильним легуванням емітера, величину  слід замінити на ефективну:

 

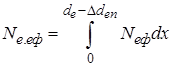,                                           (2.17)

 

де  – ефективна концентрація донорної домішки в емітері.

Одержання точних аналітичних виразів, що визначають величину , ускладнене. Тому для оцінних розрахунків значення  використовують кусково-лінійну апроксимацію, на якій прийнято такі позначення:  і  – максимальне значення ефективної концентрації й відповідно дійсне значення концентрації;

 і  – значення ефективної концентрації, що відповідає спадній частині апроксимувальної залежності й дійсне значення концентрації;

 і  – координати, відповідні концентраціям  і . Значення концентрацій  см^-3,  см^-3,  см^-3, см^-3. Апроксимувальну залежність можна визначити так:

 

      

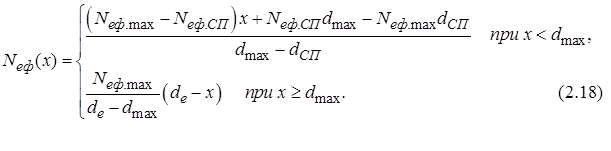
Формули для визначення  й  запишемо у вигляді

 

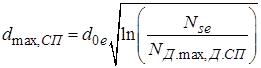.                               (2.19)

 

Якщо  см^-3, то на ділянці  значення . Підставляючи співвідношення (2.18) в (2.17) і вважаючи, що, одержимо

 

,                                 (2.20)

 

де значення  відповідає координаті , при якій .

З аналізу залежностей (2.16), (2.20) від концентрації  випливає, що значення  досягає максимуму при  см^-3.

 

Коефіцієнт передачі при інверсному включенні.

Скористаємося рис. 2.8, на якому ,,  – густини емітерного струму на відповідних ділянках [1 – 6].

 

 

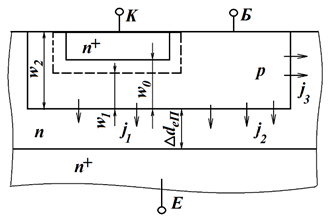
Рисунок 2.8 – Структура n-p-n-транзистора для розрахунку інверсного коефіцієнта передачі

 

Будемо вважати, що розподіл домішок у базовій області описується експоненціальною функцією  з характеристичною сталою дифузійного процесу

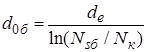,                                            (2.21)

 

n-n⁺ – перехід напівпровідникової пластини – «відображувальний» для неосновних носіїв; швидкість поверхневої рекомбінації носіїв на границях напівпровідник-метал і напівпровідник-окисел дорівнює нескінченності;   p-n – переходи мають прямокутну форму [1 – 6].

Уважаючи, що транзистор працює в активному режимі, густини струмів можна подати як:

,                         (2.22)

   ,                            (2.23)

,                                                                 (2.24)

 

де  й  – концентрації неосновних носіїв на границях шару просторового заряду емітерного переходу.

Як показує аналіз, між густинами електронного струму на відповідних ділянках (рис. 2.9) існує співвідношення:

 

.                                     (2.25)

 

Тому при розрахунках коефіцієнта передачі струму  густина струму  не враховується.

Величина  звичайно не перевищує 0,8 ÷ 0,9 і при вузькій базі ( ) можна вважати . Тоді

 

,                   (2.26)  

               

а з урахуванням співвідношень (2.22) – (2.24)

 

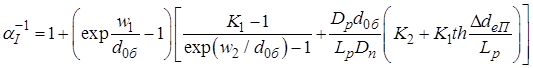,  (2.27)

 

де  й  – відношення дна й бічної площ емітерного переходу до площі частини дна колекторного переходу.

З аналізу виразів (2.26), (2.27) випливає, що  зростає при збільшенні глибини залягання емітерного переходу й концентрації домішок в емітерній області, а також при зменшенні товщини бази транзистора, поверхневої концентрації домішок базової дифузії, товщини епітаксіальної плівки
-типу й величини  й .

Стала часу коефіцієнта передачі при інверсному включенні

 

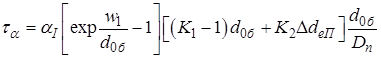.                      (2.28)

 

Формула (2.28) правильна для випадку, що найбільше часто зустрічається

 

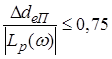,                                                (2.29)

де ;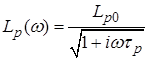

 

 – дифузійна довжина дірок при  й .

Зі співвідношення (2.28) видно, що динамічні характеристики коефіцієнта передачі  поліпшуються при зменшенні значень ,  і  й при  збільшенні концентрації домішок в емітерній області. Однак ці характеристики суттєво поступаються аналогічним характеристикам при нормальному включенні транзистора. Тому вплив сталих часу, пов’язаних із зарядом ємностей транзистора й прольотом носіїв через збіднений шар колекторного переходу можна не враховувати.

 

 

Завдання

 

Розрахувати:

1)  ширину емітера (див. рис. 2.5) використовуючи вихідні дані, що подані в табл. 2.1;

2) значення сталої часу  та граничної частоти  транзистора при інверсному включенні, використовуючи вихідні дані, які подані в табл. 2.1, за умови, що мкм, ,  мкм, 
 см²/с,  В.

 

 

 

 

Таблиця 2.1

№ варіанта	, мА		(), мкм	, мкм	, Ом·см	()	, мкм
1	4	70	0,7	12	0,2	0,8	2
2	2	35	0,4	12	0,3	0,81	3
3	1,8	70	0,5	12	0,4	0,82	4
4	3,2	60	0,6	12	0,5	0,83	5
5	3	55	0,7	12	0,6	0,84	6
6	3,5	56	0,8	12	0,7	0,85	7
7	5	80	0,9	12	0,8	0,86	8
8	4	70	1,0	12	0,2	0,87	1
9	2	35	0,4	12	0,3	0,88	2
10	1,8	70	0,5	12	0,4	0,9	3
11	3,2	60	0,6	12	0,5	0,8	4
12	3	55	0,7	12	0,6	0,81	5
13	3,5	56	0,8	12	0,7	0,82	6
14	2,5	40	0,9	12	0,8	0,83	7
15	2,2	41	1,0	12	0,2	0,84	8
16	3,5	56	0,4	12	0,3	0,85	9
17	5	80	0,5	12	0,4	0,86	1
18	4	70	0,6	12	0,5	0,87	2
19	2	35	0,7	12	0,6	0,88	3
20	1,8	70	0,8	12	0,7	0,8	4

 

Звіт повинен містити

 

1. Вихідні дані.

2. Конструктивний розрахунок геометричних розмірів емітерної області та значення сталої часу  та граничної частоти .

3. Лістинг програми.

4. Результати тестування.

5. Висновки.

 

Контрольні запитання

 

1. Наведіть порядок визначення геометричних розмірів емітерної області n-p-n-транзистора.

2. Які фактори впливають на статичний коефіцієнт передачі при нормальному включенні ? Наведіть послідовність визначення параметра.

3. Які фактори впливають на коефіцієнт передачі при інверсному включенні ? Наведіть послідовність визначення параметра.

4. Наведіть технологію виготовлення інтегрального n-p-n-транзистора.