5.3.5 Резервування з дробовою кратністю
Розрахунково-логічна схема одного з варіантів загального резервування з постійно включеним резервом і дробовою кратністю наведена на рис. 5.5.
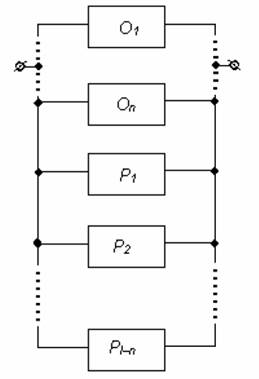
Рисунок 5.5 – Дробове резервування
У розглянутій схемі використовується n основних і (l–n) резервних
елементів (l – загальна кількість основних і резервних елементів).
При цьому (l–n)>n і, отже, ми маємо дробову кратність резервування m=(l–n)/n.
На основі раніше наведених для інших видів резервування міркувань можна одержати вираз для ймовірності безвідмовної роботи і середнього напрацювання до відмови для розглянутого випадку загального резервування ТЗ із дробовою кратністю і постійно включеним резервом при експоненційному розподілі:
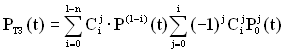 , (5.17)
, (5.17)
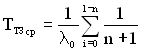 , (5.18)
, (5.18)
де ![]() – ймовірність безвідмовної роботи основного або будь-якого резервного елемента.
– ймовірність безвідмовної роботи основного або будь-якого резервного елемента.
Розглянемо тепер методи розрахунку надійності ТЗ при резервуванні заміщенням із дробовою кратністю.
Розрахунково-логічна схема для такого типу резервування при навантаженому резерві наведена на рис. 5.6.
Резервований ТЗ складається з n основних однотипних і (l–n) резервних елементів, що знаходяться в навантаженому резерві (n>(l–n)). При відмові одного з основних елементів на його місце без перерви в роботі включається один з резервних. Причому резервні елементи також можуть відмовляти. Таких заміщень, що не порушують роботу ТЗ в цілому, може бути не більше (l–n).
Середнє напрацювання до відмови такого ТЗ в припущенні абсолютно надійних перемикаючих пристроїв і рівнонадійних елементів, кожний з яких має однакову інтенсивність відмов ![]() , може бути визначене за формулою
, може бути визначене за формулою
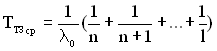 , (5.19)
, (5.19)
де l – загальна кількість основних і резервних елементів ТЗ.
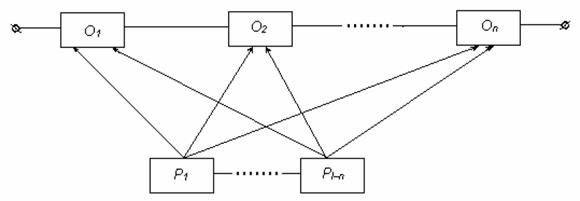
Рисунок 5.6 – Схема резервування заміщенням з дробовою кратністю
Ймовірність безвідмовної роботи резервованого ТЗ протягом часу
t для даного випадку (див. рис. 5.6) визначається з такого виразу
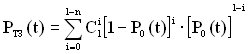 . (5.20)
. (5.20)
Розглянемо окремий випадок резервування з дробовою кратністю, а
саме мажоритарне резервування, що часто використовується в пристроях дискретної дії (рис. 5.7).
При мажоритарному резервуванні замість одного елемента (каналу) включається три ідентичних елементи (канали), виходи яких подаються на мажоритарний орган M (елемент пріоритету). Якщо всі елементи такої резервованої групи справні, то на вхід M надходять три однакових сигнали і такий же сигнал надходить у зовнішнє коло з виходу M. Якщо один із трьох резервованих елементів відмовив, то на вхід M надходять два однакових сигнали (істинних) і один сигнал помилковий. На виході M буде сигнал, що збігається з більшістю збіжних сигналів на його вході, тобто мажоритарний орган здійснює операцію визначення пріоритету або вибору за більшістю. Отже, умовою безвідмовної роботи є безвідмовна робота будь-яких двох елементів із трьох і мажоритарного органа протягом заданого часу t.
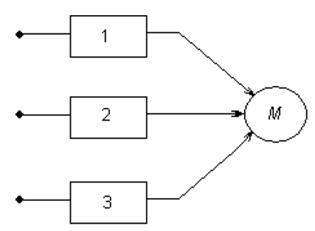
Рисунок 5.7 – Схема мажоритарного резервування заміщенням
Застосовуючи вираз (5.20) для n=2 і (l-n)=1 з врахуванням ймовірності безвідмовної роботи протягом часу мажоритарного елемента PM(t), отримаємо формулу для визначення ймовірності безвідмовної роботи ТЗ із мажоритарним резервуванням
![]() . (5.21)
. (5.21)
У випадку ненавантаженого резерву при резервуванні з дробовою кратністю (див. рис. 5.6), (помітимо, що такий вид резервування називають часто ковзним) відмова одного з n основних однотипних елементів приводить до включення на його місце одного з (l–n) резервних. При цьому за умовою елементи, що знаходяться в резерві, відмовляти не можуть до їх включення на місце відмовившого основного елемента.
Виходячи з цієї умови і з огляду на те, що в процесі нормального функціонування ТЗ у роботі знаходиться постійно n елементів, інтенсивність відмов кожного з яких дорівнює ![]() , середнє напрацювання до відмови та ймовірність безвідмовної роботи в цілому за час t при експоненційному розподілі можуть визначатися за такими виразами:
, середнє напрацювання до відмови та ймовірність безвідмовної роботи в цілому за час t при експоненційному розподілі можуть визначатися за такими виразами:
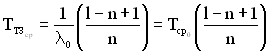 , (5.22)
, (5.22)
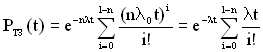 , (5.23)
, (5.23)
де ![]() – середнє напрацювання до відмови основного або резервного елемента;
– середнє напрацювання до відмови основного або резервного елемента;
![]() - інтенсивність відмови основного кола ТЗ.
- інтенсивність відмови основного кола ТЗ.
5.4 Розрахунок надійності ТЗ з інформаційною надлишковістю
У засобах цифрової обчислювальної техніки, системах телемеханіки широко використовуються так названі самокорегувальні коди, що дозволяють автоматично виявляти і виправляти помилки в одному або декількох розрядах, які з'являються в результаті збоїв або відмови елементів. При цьому відмова або збої не порушують нормального функціонування ТЗ. Зрозуміло, що пристрої, захищені самокорегувальними кодами, мають інформаційну надлишковість.
Аналіз надійності таких засобів з інформаційною надлишковістю як правило проводиться двома шляхами: наближеним і уточненим.
При наближеному аналізі надійності ТЗ ділиться на дві частини: захищену кодом від відмов і збоїв та незахищену. Незахищена кодом частина – це сукупність елементів, для яких поява хоча б одної відмови або збою призводить до спотворення інформації на виході усього пристрою в цілому. Для захищеної частини залежно від застосовуваного коду визначається допустима кількість одночасно виправних помилок K (як правило K=1) (рис. 5.8, а).
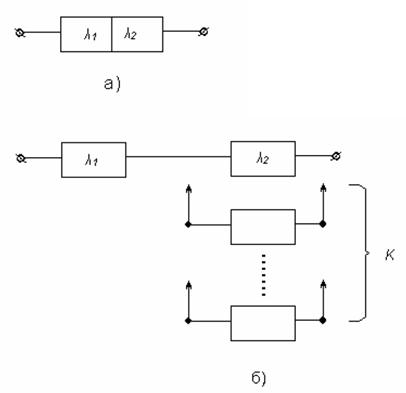
Рисунок 5.8 – ТЗ, захищені самокорегувальним кодом (наближений розрахунок надійності)
Нехай сумарна інтенсивність відмов і збоїв незахищеної частини дорівнює ![]() , а захищеної –
, а захищеної – ![]() .
.
Сформулюємо умову безвідмовної роботи ТЗ протягом часу t:
- у незахищеній частині засобу за час t не повинно відбутися жодної відмови або збою;
- у захищеній частині за той самий час може відбутися не більше K відмов і збоїв в сумі.
Ймовірність виконання цієї умови і дає ймовірність безвідмовної роботи ТЗ з інформаційною надлишковістю за час t
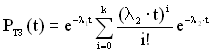 . (5.24)
. (5.24)
З умови безвідмовної роботи і виразу (5.24) випливає, що ТЗ, захищені кодом, за надійністю еквівалентні послідовному з'єднанню незахищеної частини з K-кратно резервованою (ненавантажений резерв) захищеною частиною з ідеально надійним перемикачем (див. рис. 5.8, б).
Уточнений аналіз надійності дозволяє врахувати структуру ТЗ, захищену самокерегувальним кодом. У ряді випадків захищена частина ТЗ може бути розбита на (n+N) незалежних лінійок або розрядів (рис. 5.9, а). При цьому роботоздатність захищеної частини забезпечується відсутністю спотворень інформації в n лінійках або, іншими словами, допускається одночасна відмова N будь-яких лінійок (або одночасна поява збою в N будь-яких лінійках).
Сформулюємо умову роботоздатності ТЗ протягом часу t для цього випадку. У незахищеній частині засобу за час t не повинно відбутися жодної відмови і збою. У захищеній частині за час t можуть відмовити (з'явитися збої) не більше N лінійок з (n+N) лінійок. Звідси ймовірність безвідмовної роботи ТЗ за час t буде визначатися за таким виразом
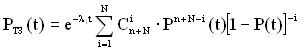 , (5.25)
, (5.25)
де 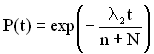 – ймовірність безвідмовної роботи однієї лінійки захищеної частини ТЗ за час t.
– ймовірність безвідмовної роботи однієї лінійки захищеної частини ТЗ за час t.
З умови безвідмовної роботи і виразу (5.25) випливає, що ТЗ, захищені кодом, за надійністю еквівалентні послідовному з'єднанню незахищеної частини з резервованою групою, складеною з n основних і N резервних (навантажений резерв) лінійок, тобто групі із ковзним навантаженим резервом з абсолютно надійним перемикачем (рис. 5.9, б).
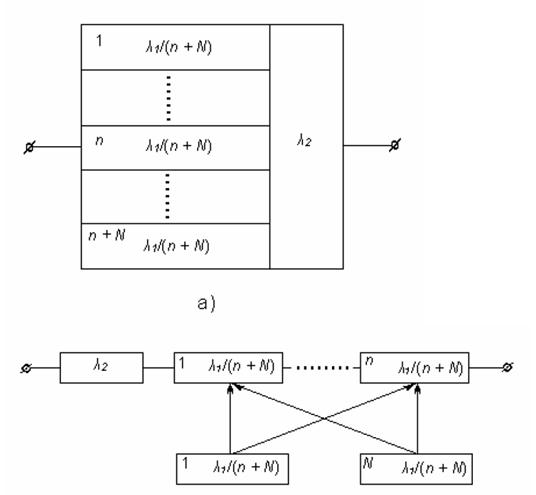
Рисунок 5.9 – ТЗ, захищені самокорегувальним кодом (уточнений розрахунок надійності)
5.5 Розрахунок надійності ТЗ із тимчасовим резервуванням
Використання тимчасового резервування поряд з розглянутими вище структурною та інформаційною надлишковістю є також ефективним способом підвищення надійності ТЗ.
При наявності тимчасової надлишковості на виконання ТЗ для будь-якої роботи відводиться час, свідомо більший, ніж мінімально необхідний. В цьому випадку можливі два варіанти використання апаратури:
а) коли виконаний обсяг роботи при настанні відмови знецінюється;
б) коли може відбуватися нагромадження роботи, тобто виконаний об’єм роботи при настанні відмови не знецінюється.
Розглянемо докладніше перший варіант. Нехай відмова апаратури знецінює роботу, виконану нею до моменту настання відмови. В цьому випадку робота буде усе-таки виконана в повному обсязі, якщо після відмови відбудеться відновлення апаратури і залишеного часу буде досить, щоб почавши виконання роботи із самого початку завершити її в установлений час. При цьому, природно, можна допустити появу декількох відмов, після кожної з яких апаратура відновлюється і щораз робота починається з початку, і так доти, доки робота не буде усе-таки виконана в повному об’ємі або не буде вичерпаний ресурс часу.
Як характеристики надійності апаратури з тимчасовою надлишковістю доцільно вибрати таке:
- ймовірність P(t, V) виконання за заданий час t роботи об’ємом V (при чому об’єм роботи виміряється мінімально необхідною тривалістю її виконання за умови відсутності відмови апаратури, а оскільки має місце тимчасова надлишковість, то V - середній час Tt,V, що витрачається на виконання роботи об’ємом V на заданому проміжку часу t. Для кращого розуміння викладеного розглянемо визначення зазначених характеристик на такому прикладі. Нехай робота, що повинна бути виконана на апаратурі, має об’єм (тривалість) V. При цьому інтервал V вкладається в проміжок часу t ціле число раз: Перевірка справності апаратури відбувається наприкінці проміжку часу V. Якщо перша перевірка установить відсутність відмови, то робота вважається успішно завершеною. У іншому випадку апаратура відновлюється (для простоти будемо вважати, що миттєво і з ймовірністю P(0) = 1), включається, і робота починає виконуватися з початку, після чого випливає друга перевірка і т. д. Відповідно до такого режиму роботи може бути побудований такий ряд розподілу: …, ..., де Оскільки робота може бути виконана за час V або за час 2V і т. д., причому події Скориставшись формулою для суми геометричної прогресії остаточно отримаємо Тут варто підкреслити, що отриманий результат збігається з формулою для навантаженого (n–1)-кратного резерву. Однак у даному випадку необхідна надійність забезпечується не додатковим включенням резервних елементів, а за рахунок виділення додатково часу на виконання роботи одним апаратом. Середній час, що витрачається на виконання роботи об’ємом V на заданому проміжку часу t легко може бути визначений як математичне сподівання випадкової величини 1. Перерахуйте основні види резервування. Дайте їх означення. 2. Які Ви знаєте основні види структурного резервування? 3. Проаналізуйте особливості пасивного і активного резервування. 4. Чим відрізняється ненавантажений резерв від постійного? 5. В чому полягає відмінність навантаженого резерву від полегшеного, резервування з цілою кратністю від резервування з дробовою кратністю? 6. Проведіть на прикладі розрахунок надійності ТЗ із ковзним резервуванням. 7. Поясніть на прикладі особливості мажоритарного резервування, його переваги та недоліки. 8. Наведіть основні відмінні риси наближеного і уточненого розрахунку надійності ТЗ з інформаційною надлишковістю. 9. Наведіть аналітичні вирази для розрахунку ймовірності безвідмовної роботи і середнього напрацювання до відмови для загального резервування ТЗ із дробовою кратністю і постійно включеним резервом при експоненційному розподілі. 10. Наведіть приклад схемної реалізації резервування заміщенням з дробовою кратністю. 11. Дайте характеристику групам заходів щодо підвищення надійності ТЗ при їхньому проектуванні. 12. Викладіть головну суть розрахунку надійності ТЗ із тимчасовим резервуванням. 13. Сформулюйте основні умови безвідмовної роботи ТЗ протягом часу t при інформаційній надлишковості. 14. Наведіть аналітичний вираз для розрахунку ймовірності безвідмовної роботи резервної групи з урахуванням ненадійності перемикача при структурному резервуванні.![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() – можливі значення часу виконання роботи (i = 1, 2, …, n);
– можливі значення часу виконання роботи (i = 1, 2, …, n);![]() – ймовірність виконання роботи за час
– ймовірність виконання роботи за час ![]() ;
;![]() – ймовірність безвідмовної роботи апаратури протягом проміжку часу V.
– ймовірність безвідмовної роботи апаратури протягом проміжку часу V.![]() (
(![]() – випадковий час виконання роботи) є подіями несумісними, то, застосовуючи теорему додавання ймовірностей, отримаємо
– випадковий час виконання роботи) є подіями несумісними, то, застосовуючи теорему додавання ймовірностей, отримаємо![]() .
.![]() . (5.26)
. (5.26)![]() – випадкового часу виконання роботи – і без виведення в остаточному вигляді дорівнює
– випадкового часу виконання роботи – і без виведення в остаточному вигляді дорівнює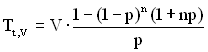 . (5.27)
. (5.27)Питання для самоконтролю