<-На зміст->

 

12.1 Методи синтезу оптимальних структур систем доступу

 

Мережа доступу, у загальному випадку, може бути подана у вигляді сукупності вузлів мережі і ліній зв’язку, що дозволяють передавати інформацію між вузлами мережі. Метою створення телекомунікаційної мережі є забезпечення обміну ін­формацією між її користувачами. Організація телекомунікаційної мережі, в якій усі користувачі з’єднані безпосередньо один з одним, економічно невигідно, тому що виникає необхідність будівництва великої кількості ЛЗ із великою сумарною довжиною використовуваного кабелю. Крім цього, коефіцієнт використання ЛЗ буде низьким. Альтернативою використання повнозв’язаної структури (в якій усі вузли мережі зв’язані безпосередньо один з одним) є застосування структури мережі, у якій передача ін­формації відбувається через проміжні вузли. У даному випадку необхідна кількість ЛЗ різко зменшується і зростає коефіцієнт використання ЛЗ.
Залежно від функцій, що виконуються вузлами, у межах заданої телекомунікаційної системи (ТКС), вони поділяються таким чином:
-      централізовані, якщо в складі системи центральний                вузол, що керує системою, до якого сходяться потоки від інших вузлів, і децентралізовані, якщо такий вузол відсутній;
-      однорангові (усі вузли рівнозначні) та ієрархічні (ТКС має багаторівневу структуру).
Телекомунікаційні системи можуть мати різну топологію            (рис. 12.1): деревоподібну, радіальну («зірка»), «загальна шина», кільцеву, багатозв’язну.
В ієрархічних ТКС різні рівні можуть мати різну топологію. У літературі під час опису топології ієрархічної мережі часто використовується нотація, запропонована J.G. Klincewicz, відповідно до якої топологія мережі позначається в такий спосіб: «топологія магістрального    сегмента»   /  «топологія   мережі   доступу».   Наприклад,

«дерево»/«зірка» означає, що магістральний сегмент має деревоподібну структуру, а абонентська ділянка – топологію «зірка».

Рисунок 12.1 – Види топології телекомунікаційних систем:
деревоподібна (а); «зірка» (б); «загальна шина» (в); кільцева (г);
багатозв’язна (д)

У процесі розробки ТКС необхідно вирішити такі питання загальномережного рівня проектування мережі, оптимальної відповідно до критерію мінімуму вартості:
- визначення топології мережі;
- вибір пропускної здатності каналів зв’язку;
- визначення процедур маршрутизації;
- визначення процедур управління потоком.
Суть задачі проектування структури ТКС і визначення оптимальних параметрів телекомунікаційних засобів, які її складають, полягає в тому, що при заданих потоках потрібно визначити параметри елементів системи і синтезувати таку її структуру, яка при дотриманні деяких вимог до характеристик могла б обслужити ці потоки. При цьому задається географічне положення користувачів ТКС і матриця потреб, що вказує інтенсивності потоків між кожною парою абонентських вузлів «джерело – адресат». Під час розв’язання даної задачі необхідно відповісти на такі запитання:
-      яку кількість концентраторів доступу (КД) необхідно установити;
- де необхідно установити КД;
- якою має бути продуктивність і ємність цих КД;
- як абоненти ТКС мають бути розподілені по зонах КД;
- яким чином абоненти ТКС мають з’єднуватися з КД і якою має бути пропускна здатність (ПЗ) каналів зв’язку (КЗ);
- яким чином КД мають з’єднуватися один з одним або з центральним вузлом і які значення ПЗ використовуваних КЗ.
Розробити математичну модель розв’язання задачі, що від­повідає на всі поставлені запитання одночасно, дуже складно. Тому проектування ТКС виконуватиметься у вигляді ітераційного процесу в такий спосіб:
-      визначається кількість і місце розташування КД і підмножини абонентів, що обслуговуються кожним з них;
- проектуються мережі доступу (абонентські мережі);
- проектується магістральний сегмент.
Ідея такого методу полягає в тому, що коли розміщення концентраторів і прив’язка терміналів до них уже зроблена, то проектування мережі доступу і магістрального сегмента відбувається незалежно і може бути зроблене окремо. Математичні моделі розв’язання задачі проектування ТКС розрізняються за критеріями проектування. Одні моделі пропонують розглядати такі параметри, як вартість будівництва мережі, вартість експлуатації мережі, її надійність і продуктивність обслуговування вимог абонентів за необхідний час, інші моделі розглядають тільки питання мінімізації вартості мережі, деякі – обидва параметри: вартість мережі і середній час затримки.
Найбільш розповсюдженим методом розв’язання задачі проектування топології мережі є побудова аналітичних моделей. За рахунок введення ряду принципових до­пущень, що дозволили використовувати методи теорії масового обслуговування, з’явилася можливість одержати в явному вигляді аналітичний вираз для середньомережевої затримки. Цей вираз був використаний для розв’язання таких задач проектування:
- задачі вибору пропускних здатностей каналів зв’язку і (ВПЗ КЗ);
- задачі розподілу потоків (РП);
- задачі вибору пропускних здатностей і розподілу потоків (ВПЗ РП).
Задача ВПЗ КЗ має точне розв’язання, якщо вартість є лінійною функцією ПЗ КЗ. У випадку, якщо величини припустимих значень ПЗ КЗ приймають ряд дискретних значень, пропонується ітераційна процедура розв’язання задачі за допомогою послідовного наближення.
У ряді моделей розв’язання задачі оптимізації ПЗ КЗ вводиться спрощення і використовується модель системи масового обслуговування типу М/М/1 з необмеженою чергою, коли пе­редній час затримки пакетів мережі і довжини черг збільшуються необмежено. У цьому випадку середній час затримки пакета в мережі визначається виразом:

                                                                       

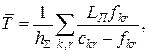
де  – сумарний потік, що надходить у мережу;
 – середня довжина пакета;
 – величина потоку в КЗ між вузлами  і ; 
 – ПЗ КЗ між вузлами  і .
Така ідеалізація допускає строге аналітичне розв’язання, що спрощує інтерпретацію результатів, але не відповідає реальним умовам функціонування мережі. Аналіз даного виразу показує, що подібна постановка задачі дає завищене значення середнього часу затримки, а обмеження відносно вузлових ресурсів, за інших рівних умов, дозволяє транспортувати по мережі більш значні інформаційні потоки. Існують методи, у яких пропонується аналітичний вираз для визначення ПЗ КЗ при таких обмеженнях: на вартість оренди КЗ, кінцеву кількість елементів буферної пам’яті, оптимальне значення щільності потоку, при якому досягається мінімум середнього часу доставки повідомлення:

                                     

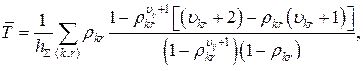
де  – завантаженість КЗ між вузлами  і ;
 – обсяг буфера для відправлення через КЗ між вузлами  і .
Задача РП, що є задачею зворотного ВПЗ, розв’язується досить ефективно методом відхилення потоку (ВП). Це дає на ви­ході оптимальний РП по КЗ, з урахуванням наявної ПЗ. При цьому кожен потік може виявитися розгалуженим, і реалізація такого розподілу на практиці досить складна. Поряд з цим існує більш простий субоптимальний метод, орієнтований на фіксовану одношляхову маршрутизацію. Відповідно до даного методу відхиляється не частина потоку, а весь потік повністю, тому в результаті всі потоки виявляться нерозгалуженими. Даний метод досить добре відбиває потреби для великих мереж, в яких частка трафіку між абонентами  і  в n-му КЗ значно менша порівняно з повним трафіком у цьому каналі.
СД, в якій здійснюється пакетна комутація, потребують для свого опису спеціального математичного апарату систем масового обслуговування. У цьому випадку необхідно контролювати ряд додаткових особливостей, що враховують реалізацію протоколів передачі, наприклад таких, як складання пакетів повідомлення на вузлі адресата. Для розв’язання задачі па­раметричної оптимізації СД можливе використання методу статистичного моделювання, суть якого полягає у використанні результатів імітаційного статистичного моделювання для фор­мулювання задачі дискретної оптимізації. Дана процедура оптимізації кількості каналів у СД зводиться до того, що у мережі імітується проходження потоку повідомлень, заданого матрицею потреби в передачі між усіма парами відправник-адресат. Зa необхідності в мережі між інцидентними вузлами вводяться додаткові КЗ, що зберігаються до кінця періоду статистичного моделювання. Зрозуміло, що із збільшенням часу моделюван­ня, кількість КЗ між сусідніми вузлами не зменшуватиметься. Далі зі структури мережі, утвореної в результаті моделювання, видаляються найменш навантажені КЗ (передбачається, що канали займаються відповідно до пріоритетів, обумовлених номерами, що присвоюються із їх появою). Потім процедура певним чином повторюється.
Зазначені методи оптимізації структури мереж мають один загальний недолік: у них не пропонується метод синтезу по­чаткової структури, що задовольняє всі обмеження. Тому було розроблено метод М-структур, у якому початкова структура заданої зв’язності генерується цілеспрямовано, за допомогою спеціального алгоритму. Спочатку на множині усіх вузлів буду­ють найкоротше зв’язане дерево (НЗД), яке далі перетвориться в надлишкову структуру заданої зв’язності. Потім оптимізують цю структуру за критерієм мінімуму вартості при виконанні усіх введених обмежень.
Іншим, не менш важливим класом задач топологічного проектування є задачі проектування топології абонентської підмережі. Методи розв’язання задач синтезу для всієї різноманітності структур (радіальної, деревоподібної або радіально-вузлової) достатньо добре досліджені, якщо на мережу не накладаються будь-які специфічні умови.
Труднощі, з якими стикаються під час практичного розв’я­зання задач проектування, обумовлені двома чинниками: великою розмірністю розв’язуваної задачі (кількість вузлів у мере­жі може доходити до 104) і відсутністю достовірних вихідних даних (наприклад, обсягів інформації на передачу) через складність формалізації усіх вимог до проектованої мережі. Першу проблему можна розв’язати за допомогою розробки ефективних методів наближеного синтезу структури мереж великої розмірності. Для розв’язання другої проблеми проводять різноманітні розрахунки при варіюванні вихідних даних у дуже широких діапазонах. Такий різноманітний синтез зручніше проводити в діалоговому режимі. Саме створення діалогових систем під­тримки проектування, що дозволяють розв’язувати різні комплекси задач структурного проектування, слід визнати найбільш перспективними.
Таким чином, формально процес проектування структури СД слід розглядати як розв’язання сукупності двох основних задач: задачі вибору структури (структурний синтез) і вибору числових значень параметрів заданої структури, що відповідають сукупності умов (параметричний синтез).
Під час організації великомасштабної СД найчастіше як ар­хітектура мережі вибирається та, яка має ієрархічну структуру. Такий вибір обумовлений тим, що він дозволяє будувати мережу з різними вимогами на різних її ділянках. Так, на магістральній ділянці висуваються більш високі вимоги до надійності, тому що пошкодження в даній частині мережі стосуються великої кількості потоків, що, у свою чергу, підвищує надмірність структури. На абонентській ділянці будувати мережі з надмірною структурою економічно невигідно, тому що збитки, у випадку тимчасового порушення зв’язності, зазвичай не перевищують витрат на ство­рення і підтримку роботоздатності надмірної структури.
Використання на магістральній ділянці кільцевої структури має  порівняно з іншими перевагу в тому, що вона забезпечує додаткову стійкість до обривів ЛЗ. У зв’язку з цим останнім часом як топологію магістральної ділянки найчастіше використовують кільцеву структуру.
Проектування структури СД із кільцевою топологією магістральної ділянки на практиці утруднене тим, що воно зводиться до необхідності розв’язання задачі комівояжера, що є NP-складною. Зменшення часу, необхідного для розв’язання задачі комівояжера, є актуальним.
Методи розв’язання задачі комівояжера можна розділити на точні і наближені. Точні методи розв’язання задачі, як правило, потребують великої кількості ітерацій, яка пропорційна факто­ріалу від розміру мережі, у той час як наближені дозволяють розв’язувати задачу за значно меншу кількість ітерацій. До точ­них алгоритмів можна віднести: лінгвістичний перебір (повний перебір); алгоритми, що використовують для зменшення кіль­кості ітерацій метод гілок і меж. До наближених належать: «жадібний алгоритм»; алгоритм із використанням методів нейронних мереж; методики еластичної мережі (ЕМ); генетичний алгоритм (ГА); «моделювання відпалу»; гібридний наближений алгоритм, що поєднує у собі такі алгоритми: «жадібний алгоритм», «моделювання відпалу» і "ви­черпного пошуку".
В останньому десятиріччі XX століття з’явився ряд різних методів розв’язання задач комбінаторної оптимізації з викорис­танням апарату теорії нейронних мереж, які дозволяють успішно розв’язувати дані задачі. З аналізу цих методів можна зробити висновок про те, що ефективність і якість одержуваних результатів при застосуванні методів нейронної мережі підвищується. Подальшим, найбільш ефективним шляхом розвитку методології є гібридизація цих методів з позначково-евристичними. Ефективність застосування різних наближених методів розв’язання задачі комівояжера досліджувалася на прикладі методів теорії нейронних мереж, ЕМ, ГА і «моделювання відпалу», а також порівняння цих методів з евристичним гібридним алгоритмом, що, як було зазначено, поєднує в собі такі алгоритми, як «жадібний алгоритм», «моделювання відпалу» і «вичерпного пошуку».
За результатами експериментального порівняння алгоритмів можна зробити такі висновки. Усі методи кращі або еквівалентні стандартному методу моделювання відпалу. ГА, серед інших є кращим, до нього за своїми показниками близькі гібридний наближений алгоритм і методика ЕМ. Алгоритм нейронної мережі за ефективністю гірший, ніж метод ЕМ. Іншим важливим параметром є час розрахунку. Він поділяється на дві складові: кількість операцій (послідовно виконуваних) в одній ітерації для заданої розмірності задачі; і кількість ітерацій, необхідний для збіжності.
Зі сказаного вище можна зробити висновок про те, що в умовах наближеного (пошуку локального оптимуму) розв’язання задачі синтезу мережі взагалі використання точних алгоритмів розв’язання задачі комівояжера є неефективним з погляду часових витрат.
Серед існуючих методів наближеного розв’язання задачі комівояжера особливий інтерес являє собою метод ЕМ. Цей наближений метод належить до методів дискретної оптимізації в евклідовому просторі (при розміщенні місць на площині). Еластична мережа може бути подана як деяка кількість точок, з’єднаних еластичною гумовою ниткою так, щоб утворити кільце. Ідея методу полягає в тому, що, використовуючи ітеративну процедуру, круговий замкнутий ланцюг поступово і неоднорідно подовжують доти, поки він не проходитиме досить близько до всіх місць, визначаючи таким чином маршрут.
Іншою важливою задачею, що розв’язується під час проектування ієрархічної СД, є задача визначення місць розміщеним КД і близька до неї задача прив’язки користувачів до КД.
Під час розміщення об’єктів зв’язку, особливо тих, які забезпечують доступ (маршрутизатори, концентратори) як локального, так і більш розподіленого (глобального) функціонування, дово­диться розв’язувати задачу мінімізації загальної суми відстаней між цими об’єктами. Ця задача зводиться до оптимізаційної задачі Штейнера-Вебера про розміщення об’єктів зв’язку на  площині. Для розв’язання цієї задачі пропонується рекурсивна процедура оптимізації за критерієм мінімальної сумарної зваженої відстані з використанням параболічної апроксимації цільової функції поблизу точки стану. Даний алгоритм може бути застосований для одно- та m-вимірної ситуації, де m – кількість засобів, що заново вводяться. Запропонована методика може бути використана як під час обладнання неохоплених засобами зв’язку територій, так і під час дооснащення вже існуючих мереж локального або глобального характеру.
Під час комплексного розв’язання задачі визначення місць розміщення концентраторів і прив’язки абонентів до них можливі два сценарії дій. Відповідно до першого сценарію серед існуючих вузлів, орієнтуючись на їх взаємне розташування, вибирають місця установки КД. Далі до цих вузлів приєднують інші вузли, які розбивають по групах. Відповідно до іншого сценарію дій усю множину вузлів, орієнтуючись на їх взаємне розташування, розбивають на групи, після чого роблять вибір місця установлення КД. Таким чином, ці задачі зводяться до класичних задач класифікації і кластеризації, відповідно.
Суть задачі класифікації полягає в тому, що задається деяка множина еталонів , обумовлених вектором ознак  після чого вся множина об’єктів  розбивається на непересічні підмножини за ступенем відповідності об’єкта  еталону .
Суть задачі кластерізації в тому, що існуюча множина об’єктів  розбивається на непересічні підмножини, які мають відповідність об’єктів один одному всередині підмножини.
Для розв’язання задачі класифікації необхідно ввести розв’язувальне правило, відповідно до якого визначається ­належність об’єкта даному класу, обумовленому еталоном. Як розв’язувальне правило найчастіше використовується максимум функції відповідності об’єкта еталону.

 

<-На зміст->