<-На зміст->

 

12.2 Постановка задачі синтезу структур систем доступу

 

Розглянемо постановку задачі синтезу структури СД і визначення параметрів засобів телекомунікації, що складають систему, оптимальних відповідно до критерію мінімуму вартості.
Припустимо є множина  абонентських систем (АС) джерел інформаційних потоків. Позначимо:
 – обсяг вимог, що виникає в одиницю часу у абонента  і підлягає передачі абонентові , біт/с;
 – матриця потреб у передачі трафіку між  і ;
 – географічні координати пункту перебування абонента ;
 – множина пунктів, де можливе розміщення КД до магістрального сегмента мережі;
 і   – потужності множин А і Z, відпо­відно;
 – кількість вузлів, у яких необхідно організувати вузол доступу (ВД) до магістрального сегмента мережі;
  – відстань між пунктами  і , км.
Для СД на базі провідних ЛЗ величина  залежить від структури мережі. При цьому можливі два випадки:
- якщо пункти  і  з’єднані безпосередньо, то можна вважати рівними відстані між  і  з урахуванням подовження ЛЗ унаслідок рельєфу місцевості (колодязі, тунелі тощо);
- якщо пункт  з’єднаний з пунктом  через ряд транзитних пунктів (як, наприклад, при деревоподібній структурі), то  береться рівним сумі довжин усіх транзитних ділянок ЛЗ, що з’єднує  з ;
 – набір ПЗ КЗ, застосування яких можливе для організації низькошвидкісного сегмента мережі;
 – набір ПЗ КЗ, застосування яких можливе для організації магістральної ділянки мережі.
До найважливіших показників, що враховуються під час проектування телекомунікаційних мереж, слід віднести: вар­тість (приведені витрати), надійність мережі, середній час затримки передачі повідомлень між довільними вузлами мережі. Розглянемо ці показники докладніше.
Введемо величину приведених витрат на організацію й експлуатацію прямого КЗ між пунктами  і

                                                       

де  – капітальні витрати на будівництво ЛЗ;
 – норма­тивний коефіцієнт окупності капітальних вкладень;
 – екс­плуатаційні витрати на підтримку КЗ.
З достатньою для практики точністю можна вважати, що капітальні витрати на будівництво одиничної ЛЗ довжиною  описуються формулою

                                                                                       
де k – вартість одного кілометра залежно від типу КЗ, а залежність експлуатаційних витрат для такого КЗ можна подати виразом

                                                                            
де b – питомі експлуатаційні витрати, приведені на один кіло­метр;
с – пропускна здатність КЗ між пунктами  і ;
 – питомі витрати на одиницю ПЗ;
 – статичний коефіцієнт
Зробивши підстановку (12.4) і (12.5) у (12.3), одержимо вираз для величини приведених витрат на створення КЗ між пунктами  і :

        

де  – величина витрат на будівництво і підтримку роботоздатності ЛЗ довжиною  між пунктами  і ;
 – величина витрат на організацію КЗ між пунктами  і  із пропускною здатністю 
Опираючись на наведені вище параметри, додатково введемо такі позначення:
 – матриця приведених витрат на будівництво ЛЗ між  і ;
 – матриця приведених витрат на будівництво ЛЗ між пунктами, де організований ВД на магістральній ділянці мережі;
 – зведені витрати на організацію КЗ із пропускною здатністю  на низькошвидкісному сегменті мережі;
 – зведені витрати на організацію КЗ із пропускною здатністю  на магістральній ділянці мережі.
Оцінимо зведені витрати на організацію ВД на магістральному сегменті. Дана величина залежить від типу використо­вуваного устаткування і необхідної продуктивності ВД і може бути визначена з виразу

                                                            

де  – капітальні витрати на організацію ВД;
 – екс­плуатаційні витрати на підтримку роботоздатності ВД;
П – продуктивність ВД.
На практиці капітальні витрати на організацію вузла доступу
мають нелінійну залежність від величини необхідної продуктивності: зі збільшенням продуктивності вузла питомі витрати на одиницю продуктивності зменшуються. Виходячи з цього капітальні витрати на організацію ВД пропонується оцінити таким співвідношенням:

                                                                           

де  – коефіцієнт пропорційності, ;
 – статичний ко­ефіцієнт, що враховує нелінійність,
Якісно аналогічну характеристику має залежність експлуатаційних витрат від продуктивності вузла і їх величину пропонується оцінити таким співвідношенням:

                                                                           

де  – коефіцієнт пропорційності, ;
 – коефіцієнт, що враховує нелінійність,
Додавши (12.8) та (12.9), одержимо вираз для оцінки зведених витрат на утримування ВД необхідної продуктив­ності:

                                                                 

Необхідну продуктивність для вузла  можна оцінити таким виразом:

                                              

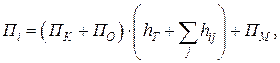
де  – кількість операцій, необхідних для здійснення про­цедур управління потоком й іншими процедурами управління, що здійснюються над пакетом;
 – кількість операцій, необхід­них вузлу доступу для обслуговування одного пакета;
 – сумар­ний транзитний потік, що проходить через вузол, біт/с;
 – кількість операцій, необхідних вузлу для здійснення управління маршрутизацією і розрахунку маршрутних таблиць.
Під час синтезу структури магістрального сегмента ієрархічної СД до неї висуваються більш високі, ніж на низькошвидкісній ділянці, вимоги щодо надійності. Традиційно на­дійність структури мережі оцінюється коефіцієнтом зв’язності відповідного їй графа і визначається в такий спосіб: граф G називається k-зв’язним , якщо при відмові не більше ніж  вузлів він залишається зв’язним. Аналогічним чином, граф G називається k-реберно-зв’язним, якщо при відмовах не більше ніж  довільних ребер він залишається зв’язним. Слід зазначити, що якщо граф k-зв’язний, то він і k-реберно-зв’язний. Зворотне твердження у загальному випадку неправильне. Відповідно до теореми Менгера, якщо граф k-зв’язний, то існує не менше ніж k різних маршрутів між будь-якою парою його вершин. Ця властивість використовується при практичній оцінці  зв’язності графа . Часто під час синтезу структури мережі задаються значенням
Таким чином, ставиться задача знайти таку структуру мережі заданої зв’язності , місця установки ВД і пропускну здатність для кожного з каналів , при яких забезпечується передача заданих трафіків між будь-якою парою вузлів  із середньою затримкою Т, що не перевищує допустиму. Приведені витрати на мережу при цьому мають бути мінімальними.
Математичну постановку задачі розглянемо пізніше, під час розгляду методів розв’язання відповідних задач.

 

<-На зміст->