<-На зміст->

 

12.3.1 Задачі синтезу топології

 

Задача синтезу топології СД є першим етапом проектуван­ня. У цьому розділі буде розглянуто різні методи синтезу, які є досить загальними і придатними для проектування різноманіт­них мережевих систем. Синтез топології розподіленої СД, під якою розуміють конфігурацію мережі каналів і розташування керувальних комплексів разом з їх імовірнісно-часовими характеристиками і структурно-надійнісними параметрами, має враховувати масштабність, географічне положення, обмеження і специфіку системи, що проектується.
Задача вибору оптимальної топології мережі, що забезпечує найкращий у значенні обраного критерію (або критеріїв) варіант розташування компонентів мережі, який би відповідав усім ви­могам, що висуваються до мережевого трафіку, може мати кілька постановок. Як критерій можуть виступати вартісні, часові, надійнісні та інші параметри.
Загальна постановка задачі топологічного синтезу, харак­терна для проектування нової мережі, така. Задано перелік і розташування кінцевих пунктів АС ; матрицю зовнішнього графіка , елементи якої визначають характеристики ін­формаційного потоку між АС  та ; вартість й експлуатаційні характеристики каналів і устаткування вузлів комутації; вимоги до надійності, живучості і якості обслуговування. Необхідно позначити структуру мережі, що забезпечує зв’язок між АС із заданою якістю при мінімальних (зведених) витратах W на побудову мережі. Це так звана однокритеріальна постановка задачі.
Як вже раніше зазначалося, мережа може мати таку топологію:
- радіальна («зірка»);
- деревоподібна;
- радіально-вузлова;
- шинна;
- кільцева;
- багатозв’язна.
Залежно від типу використовуваної топології розрізняються і методи синтезу її оптимальної структури. Розглянемо їх за наведеним списком.
Під час синтезу топології мережі «зірка» задача розв’язується в такій постановці: задана множина абонентських терміналів ,  де п – кількість терміналів, що задані своїми географічними координатами  які необхідно з’єднати безпосередньо з центральним вузлом  ЛЗ. У даній постановці задачі є одне єдине рішення і немає альтернативних варіантів, а отже, дана задача не є задачею оптимізації і надалі розглядатися не буде.
Під час синтезу інших з наведених вище типів топології аналогічно попередньому випадку задача розв’язується в такій постановці. Задана множина АС  , де п – кількість АС, які задані своїми географічними координатами  Необхідно з’єднати АС між собою ЛЗ так, щоб забезпечити можливість передачі інформації від усіх вузлів-джерел до усіх вузлів-одержувачів цієї інформації, при цьому вузли можуть одночасно бути як джерелами інформації, так і одержувачами. Додатково під час синтезу топології висувається ряд додаткових обмежень залежно від типу топології, яку необхідно одержати.
Під час синтезу деревоподібної топології додатковою є вимога, щоб отримана топологія мала мінімальну вартість, що одночасно є і критерієм оптимізації. Дана вимога призводить до обмежень, мережа була однозв’язною і не мала циклів, тому що в останньому випадку існують ЛЗ, усунення яких зменшує вартість отриманої структури і не приводить до порушення вимоги зв’язності.
Під час синтезу радіально-вузлової топології серед множини АС або додатково до неї вибираються місця установлення КД, які з’єднуються з центральним вузлом безпосередньо, щоб утворити топологію «зірка», інші АС з’єднуються безпосередньо з центральним вузлом або безпосередньо з одним з КД, з’єднання абонентських станцій безпосередньо одна з одною не допускається. Хоча радіально-вузлова структура є окремим випадком деревоподібної, однак наведена постановка задачі синтезу не дозволяє використовувати для її розв’язання методи синтезу структур, розроблені для деревоподібних мереж. Додатково під час синтезу топології можуть висуватися обмеження на кількість терміналів, які підключаються до кожного з КД, обмеження на величину інформаційного потоку, переданого по ЛЗ, також може допускатися приєднання КД до інших КД з обмеженням на максимальну кількість концентраторів у шляху від АС до центрального вузла. Під час синтезу радіально-вузлової топології враховується вартість установлення КД.
Під час синтезу шинної топології допускається з’єднання абонентських станцій безпосередньо одна з одною і додатково висувається вимога, щоб кожен вузол мережі з’єднувався не більше ніж з двома іншими вузлами. У результаті розв’язання даної задачі синтезу одержуємо структуру, в якій усі вузли мережі з’єднані в ланцюжок, при цьому тільки два крайні вузли в ланцюжку мають з’єднання тільки з одним вузлом, інші мають з’єднання з двома іншими вузлами. Аналогічно попередньому випадку шинна топологія теж є окремим випадком деревоподібної топології, однак уведення додаткового обмеження змінює математичну модель задачі синтезу і не дозволяє використовувати для її розв’язання методи синтезу структур, розроблені для деревоподібних мереж.
Під час синтезу кільцевої топології допускається з’єднання АС безпосередньо одна з одною і додатково висувається вимога, щоб кожен вузол мережі обов’язково мав з’єднання саме з двома іншими вузлами. У результаті розв’язання даної задачі синтезу одер­жуємо структуру, у якій усі вузли мережі з’єднані в кільце.
Під час використання як критерію оптимізації критерію мінімуму сумарної довжини ліній зв’язку задача синтезу шинної і кільцевої  топології зводяться до задач знаходження на графі мережі гамільтонова ланцюга і циклу мінімальної ваги, відповідно, і мають схожі методи розв’язання.
Під час синтезу баготозв’язної топології (в іноземній літера­турі дана топологія називається «mesh») допускається, щоб на графі мережі існували цикли, які приводять до появи альтернативних шляхів доставки інформації. Виникнення задачі синтезу багатозв’язної топології зумовлене необхідністю підвищення структурної надійності мережі за рахунок уведення додаткових ЛЗ, використання даної топології дозволяє також зменшити середню довжину шляху між АС, а отже, – час затримки по­відомлення в мережі. До найважливіших параметрів якості, що враховуються під час синтезу баготозв’язної структури, слід віднести: вартість (зведені витрати, які враховують капітальні витрати на організацію мережі з заданою структурою, і витрати на експлуатацію мережі), надійність мережі, часові й імовірнісні характеристики передачі повідомлення між АС. Для спрощення задачі синтезу та її практичного розв’язання визначають голов­ний показник ефективності, що підлягає оптимізації, а інші показники переводять у розряд обмежень. Залежно від основного показника ефективності розрізняють такі варіанти постановки задачі: синтез топології за критерієм часу, синтез топології за критерієм вартості, синтез топології за критерієм надійності (слід зазначити, що для комерційних СД найбільш прийнятним є синтез за критерієм вартості, а для систем спеціального при­значення – синтез за критерієм часу або надійності).
Синтез деревоподібної топології
Найбільш поширений клас мереж доступу складають дерево­подібні мережі, структура яких є деревом або сукупністю дерев з коренями, що відповідають місцям розміщення концентраторів.
Така структура виникає, коли при підключенні АС використовують віддалені концентратори. Застосування багатопунктових ЛЗ дозволяє скоротити капітальні витрати на створення СД, підвищити коефіцієнт використання КЗ, скоротити загальну довжину ЛЗ порівняно з СД радіальної структури, в якій використовуються виділені КЗ для всіх АС.
Задача синтезу мережі доступу в класі деревоподібних мереж формулюється таким чином. Задано: множина АС  що характеризуються своїми географічними координатами місцезнаходження  і матриця зовнішнього трафіку , а також місця розміщення концентраторів  і зв’яз­ки абонентів до концентраторів , . Відомі приведені витрати на передачу інформації  від пункту  до пункту , де  – ПЗ КЗ між  та , а також матриця приведених витрат  на будівництво ЛЗ між  та . Потрібно синтезувати структуру абонентської мережі в класі деревоподібних структур мінімальної вартості при обмеженнях на сумарний потік (трафік)  у кожній ЛЗ :  де  – ПЗ багатопунктової ЛЗ;  визначається як сума інформаційних потоків від усіх вузлів, що прямують через ЛЗ між  та   на шляху від кінцевих вершин до кореня дерева і потоку , обумовленого АС .
Розглянемо найбільш важливі алгоритми розв’язання цієї задачі – алгоритми Краскала та Прима. Зазначимо, що в задачі Краскала та Прима не вводяться обмеження на ПЗ ЛЗ і тому відсутнє обмеження на сумарний потік , що передається по ЛЗ . Таким чином, алгоритми Краскала та Прима дозволяють синтезувати найкоротше зв’язане дерево або найкоротші зв’язані мережі (НЗМ) без обмежень. Практично набагато важливішою є задача синтезу НЗД з обмеженнями на сумарний потік , які обумовлено ПЗ КЗ .
Синтез деревоподібної топології без урахування інформаційних потоків
Для розв’язання даної задачі за допомогою алгоритмів зна­ходження кістякового дерева мінімальної ваги в графі необхідно перейти до моделі у вигляді графа. При переході до графа ме­режі як вершини графа візьмемо АС, як ребра графа – ЛЗ, яким припишемо ваги, що дорівнюють вартості будівництва ЛЗ  між  і . У результаті проведеної операції ми одержимо повнозв’язаний зважений граф Г (V, Е, D), де V – множина вер­шин, Е – множина ребер, D – ваги ребер. Застосувавши для даного графа алгоритм Краскала або алгоритм Прима, ми одержи­мо суграф, що є деревом мінімальної ваги і є топологією мережі з мінімальною довжиною ЛЗ.
Перевага алгоритму Прима полягає в простоті реалізації процедури побудови НЗМ як при обчисленнях ручним спосо­бом, так і за допомогою ЕОМ. Разом з тим, алгоритм Прима є досить універсальним, тому що довжина за необхідності може бути замінена вартістю, пропускною здатністю або кількістю канало-кілометрів і т. д.
Побудова НЗМ за алгоритмом Прима розв’язує задачу ство­рення мережі з мінімальною довжиною ЛЗ безпосередньо між вузлами. Разом з тим, у загальному випадку подібна мережа не є найкоротшою, яка взагалі може бути створена. Зокрема давно відома задача Штейнера: знайти НЗМ для заданої множини вузлів, допускаючи додання в будь-якому місці додаткових транзитних вузлів. Розв’язання цієї задачі, яке було б зручним для проектування мереж зв’язку, до цього часу не існує. Відомо лише декілька необхідних умов і певних міркувань, що не дають, однак, ефективного розв’язання. Тому нижче пропонується наближений метод розв’язання задачі Штейнера, який базується на використанні ряду допущень і називається методом допоміжних трикутників.
Відповідно до алгоритму Прима будуємо НЗМ без додаткових вузлів. У побудованій мережі вибираємо умовні трикутники, дві сторони яких є необхідними ребрами за алгоритмом Прима. В умовних трикутниках робимо додаткові побудови, уводячи транзитні вузли. Розглянемо це на прикладі.
Будуємо, відповідно до алгоритму Прима, НЗМ без додаткових вузлів. На підставі отриманих даних побудуємо НЗМ (рис. 12.2). З рисунка видно, що виділяються чотири умовні трикут­ники: .
Використовуючи наведені вище правила, побудуємо НЗМ. З елементарної математики відомо, що довжина медіани на сторону а дорівнює:  Величина кутів навпроти сторони a:  навпроти сторони b:  навпроти сторони с:  Радіус вписаного кола  півпериметр умовного трикутника

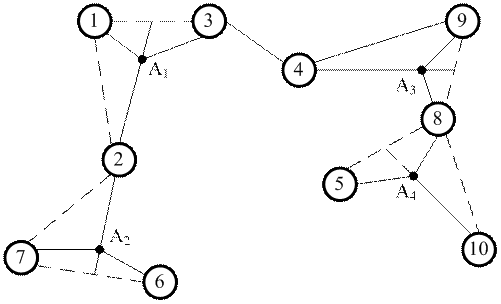
Рисунок 12.2 – Наближений метод розв’язання задачі Штейнера

Провівши всі необхідні обчислення, знаходимо, що для даної системи з десяти вузлів можна побудувати мережу з введен­ням чотирьох додаткових транзитних вузлів  При цьому загальна довжина мережі становить 42,8 одиниць, тобто скорочується на 8 %. Якщо таке скорочення довжини мережі є економічно вигідним, то знайдене розв’язання буде доцільним.
Ідеальна НЗМ у розглянутому прикладі становить 41,1 одиниці, тобто помилка обчислень за наближеною методикою не перевищує 4,14 %.
Говорячи про НЗМ, не можна не відзначити можливі об­меження, що можуть накладатися під час синтезу структури мережі умовами її функціонування і вимогами проектного завдання, а також необхідно розкрити такі поняття як довжина або «вага» ребер. Інакше постановка і розв’язання задачі синтезу структури мережі будуть неповними.
Синтез багатозв’язної топології без урахування потоків
Задано: розміщення АС ,  матриця вартості будування ЛЗ  між пунктами  і . Потрібно визначити структуру мережі  з коефіцієнтом зв’язності , щоб мінімізувати витрати на створення мережі.
Як видно з наведеної постановки задачі, в ній не враховуються витрати на організацію передачі інформаційних потоків і допустимі величини для ПЗ КЗ. Таким чином, дана задача зводиться до знаходження такої топології мережі, в якій сумарна довжина використовуваних ЛЗ була б мінімальною при обмеженнях на величину структурної зв’язності.
Для розв’язання цієї задачі необхідно знайти таку множину ЛЗ, які з’єднують між собою вузли мережі, щоб структурна зв’язність мережі дорівнювала необхідній величині і сумарній довжині ЛЗ, яка була мінімальною. Для цього можна запропо­нувати такий алгоритм.
Будуємо НЗД. Отримана топологія мережі має мінімальну
сумарну довжину ЛЗ і є однозв’язною, тому нам необхідно підвищити її зв’язність за рахунок уведення додаткових ЛЗ.
Визначаємо множину вузлів мережі, що мають зв’язок тільки з одним сусіднім вузлом, тобто визначаємо множину вершин еквівалентного графа зі ступенем, що рівнює 1.
Будуємо НЗД, що з’єднує між собою множину вузлів, знайдену на попередньому кроці.
Отримана топологія мережі є двозв’язною і має мінімаль­ну сумарну довжину використовуваних ЛЗ. Слід зазначити, що отримана структура є як двозв’язною, так й дворебернозв’язною.
Даний алгоритм застосовується в модифікованому методі М-структур для одержання початкової топології однорангової СД. До недоліків такої постановки задачі і методів її розв’язання можна віднести:
під час синтезу даної топології не враховуються величини потоків, які передаються по ЛЗ;
не враховуються витрати на організацію КЗ з необхідної для передачі таких потоків ПЗ;
не враховуються середня довжина шляху передачі повідомлення через мережу і величина часу затримки повідомлення в мережі.
Нижче наводиться алгоритм синтезу топології мережі, в якому враховуються наведені вище параметри, до більш детального розгляду яких ми і переходимо.

 

<-На зміст->