<-На зміст->

 

12.3.2 Задача розподілу потоків

 

Суть задачі розподілу потоків (РП) в тому, що для відомої топології мережі і ПЗ КЗ слід визначити шляхи передачі інфор­маційних потоків та їх величини, які забезпечують максимум ступеня відповідності вимогам щодо передачі інформації від дже­рел до споживачів. У деяких випадках задача розподілу потоку розв’язується при невідомих значеннях пропускних здатностей каналів.
Розглянемо загальну постановку задачі розподілу потоків.
Припустимо, задано: множина вузлів А; множина вузлів-джерел інформації ; множина вузлів-споживачів інформації ;  множина транзитних вузлів ; множина ЛЗ, що з’єднують між собою вузли, ПЗ КЗ  між суміжними вузлами  і  і вимоги до передачі інформації А між вузлами  і . Необхідно визначити шляхи передачі інформації від  до  і величини потоків у КЗ  так, щоб величина потоку в КЗ не перевищувала його ПЗ , щоб задовольнялися вимоги до передачі інформації і досягався максимум певного параметра якості передачі.
Одним з параметрів якості передачі є ступінь використання продуктивності мережі. У цьому випадку постановка задачі буде такою.
Розв’язання задачі розподілу потоків для розгалужених потоків
Інформаційний потік, що передається між парою вузлів «джерело-споживач» декількома шляхами, називається розгалуженим потоком. Такі потоки виникають тоді, коли в мережі застосовується багатошляхова стратегія маршрутизації.
Розглянемо постановку задачі. Задано: топологія мережі , ПЗ КЗ  і матриця вимог  . Необхідно вибрати такі маршрути для передачі всіх інформаційних потоків, що надходять у мережу, і розрахувати величини потоків у ЛЗ  таким чином, щоб мінімізувати середній час затримки передачі повідомлення в мережі

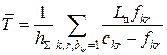
на множині всіх потоків , що відповідають матриці вимог Н і умові , . Ця задача відноситься до задач опуклого програмування, тобто існує єдиний мінімум, що є глобальним. Його можна знайти методом найшвидшого спуску, що, однак, вимагає значних обчислювальних витрат. Для розв’язання задачі РП Л. Клейнроком і М. Герлоєм був запропонований метод ВП.
Метод ВП призначений для знаходження мінімуму (екстре­муму) нелінійної функції  за змінними , де  – век­тор багатопродуктового потоку, що відповідає умові , .
Розглянемо теоретичні основи методу. Припустимо, що функції  безперервні разом зі своїми першими похідними. Визначимо необхідні і достатні умови стаціонарності . Для будь-якого нескінченно малого збурення , такого, що  – також припустимий потік, виконуєть­ся нерівність  Загальне збурення, що діє на величину  (яке визначаємо як відхилення потоку), мож­на подати як опуклу комбінацію  і будь-якого іншого потоку . Тоді новий потік  після збурення , де , F – множина припустимих потоків . Якщо , то відхилення потоку нескінченно мале. Для  маємо

                           

де ;
.
З рівняння (12.12) і умов стаціонарності випливає, що потік  є стаціонарним, якщо

                                                                              

Можна задавати різні збурення, що діють лише на одну з вимог , при цьому потік  має бути стаціонарним відносно кожного з них. Звідси випливає, що  – стаціонарний потік, якщо для всіх  виконується нерівність

                                              

де F – множина припустимих потоків.
Умови (12.13) і (12.14) еквівалентні. Умову (12.14) можна пере­писати в іншому вигляді:

                    

Але оскільки , то умова (12.15) матиме вигляд

                                                         
Аналогічно

                                                      

Умови (12.16) і (12.17) легко перевірити: права частина оці­нюється точно, а ліва частина потребує обчислення потоків по найкоротших шляхах у метриці . Якщо подати потік як зважену комбінацію потоків по всіх шляхах, то умову (12.17) можна записати в іншому вигляді:

                                                        
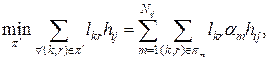
де  – будь-який маршрут;
 – усі шляхи, використовувані для передачі вимоги ;
 – вага шляху ;
 – загальна кількість маршрутів між .
Наведемо опис методу ВП. Розглядатимемо FD як оператор ВП, що відображає потік в інший потік і визначається в такий спосіб:

де  – відповідним чином обраний потік ;
 – величина кроку.
Очевидно  Ha основі співвідношень (12.15)-(12.17) легко показати, що для невиродженої і обмеженої знизу функції  наведені нижче умови є достатніми для збіжності методу ВП до стаціонарної точки:
;
 стаціонарна, де .
Алгоритм ВП складається з таких кроків:
- знаходимо припустимий початковий потік ;
- приймаємо п = 0;
- визначаємо метрику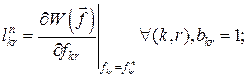
- знаходимо найкоротші шляхи  між усіма вузлами в метриці ;
- визначаємо потік по всіх найкоротших шляхах  у метриці ;
- знаходимо ;
- обчислюємо оптимальне значення  з умови

Оптимальне значення  можна знайти за допомогою будь-якого придатного методу пошуку (наприклад, за допомогою ме­тоду Фібоначчі).
Якщо  де  – задана точність, так завершується робота алгоритму, інакше  і переходимо до кроку 3.
Отже, алгоритм ВП збігається до стаціонарних точок, однак єдиною стаціонарною точкою стійкої рівноваги є локальний мінімум, і, отже, алгоритм сходиться до локального мінімуму. Коли  строго опукла, то алгоритм ВП сходиться до глобального мінімуму. Якщо ж  увігнута або квазіувігнута, то локальний мінімум відповідає крайнім точкам (тобто потокам  по найкоротших шляхах). Ця властивість значно спрощує метод ВП і прискорює його збіжність.
Розв’язання задачі розподілу потоків для нерозгалужених потоків
Розглянута в попередньому підрозділі задача РП для розгалужених потоків і метод її розв’язання дозволяє оптимально використовувати ПЗ КЗ і мінімізувати величину середньомережевої затримки повідомлення. Однак отриманий РП на практиці реалізувати дуже складно. Тому нижче розглянемо задачу РП для фіксованої стратегії маршрутизації, коли інформація від вузла-джерела до вузла-споживача передається по одному шляху.
Потік називається нерозгалуженим, якщо потік між парою «джерело-одержувач», тобто трафік , передається тільки по одному шляху. Введення обмеження на нерозгалуженість скорочує множину допустимих потоків, що приводять його до кінцевої множини. Безперервні методи, подібні до методу ВП, у цьому випадку непридатні, а дискретні методи дуже складні. Тому необхідно розробити ефективні субоптимальні методи. Для великих і збалансованих мереж можна успішно застосовувати моди­фікацію методу ВП.
Мережа називається великою, якщо має велику кількість вершин, і збалансованою, якщо елементи  матриці Н не занадто відрізняються один від одного. Для більш чіткого визначення збалансованості візьмемо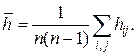
Припустимо, m – відношення між максимальною і середньою вимогами:

при цьому . Мережа називається збалансованою, якщо .
Об’єднаємо ці два визначення в поняття великої і збалансованої мережі. Уведемо коефіцієнт :

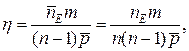
де п – кількість дуг графа;
 – середня щільність дуг на одну вершину графа;
 – середня довжина шляху в графі за умови, що усі вимоги передаються по найкоротших шляхах (тут під довжиною шляху мають на увазі кількість дуг у шляху):

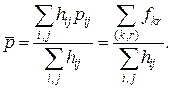
Мережа називається великою і збалансованою, якщо .
Щоб обґрунтувати таке визначення, розглянемо для довільного
потоку відношення сумарного потоку  у дузі  до відповідного потоку , що задається вимогою . Знайдемо середню величину цього відношення по всіх дугах:

                                

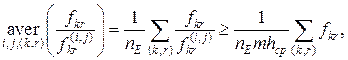
де aver позначає процедуру усереднення. Але, як показано


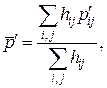
де  – середня довжина шляху в графі при заданому способі маршрутизації;
 – довжина шляху від  до  при даному способі маршрутизації.
При цьому , причому  залежить від конкретного розподілу шляхів, тоді як  залежить тільки від структури і матриці вимог. Рівняння (12.19) можна переписати в іншому вигляді:

                                             

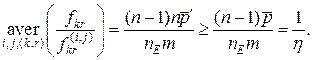
З виразу (12.20) випливає така властивість. У великій і зба­лансованій мережі внесок однієї вимоги  у загальний потік у дузі  можна розглядати як величину нескінченно малу. Для того, щоб застосовувати метод ВП для нерозгалужених потоків у великій і збалансованій мережі, розглянемо нову версію методу ВП, яку визначимо як композицію відхилень, що включають щоразу дію тільки однієї вимоги . Отже, припустимо, що потік  нерозгалужений, трафік  проходить по шляху , а  – найкоротший маршрут між вузлами  і  у метриці . Відповідно до методу ВП, частина потоку вимоги  відхиляється зі шляху  на шлях  так, щоб цільова функція де потік  передається по шляху , a  – по шляху . Перепишемо цей вираз:

                             

де  містить залишкові члени порядку малості вище, ніж 1.
Відповідно до властивості збалансованості члени  можна вважати нескінченно малими 1-го порядку, а член  – нескінченно малим 2-го порядку. Тому оскільки величина  є від’ємною і досить великою, то членом  можна знехтувати і мінімум у формулі (12.21) досягається на границі при . Отже, метод ОП зберігає властивість нерозгалуженості потоку. Проте якщо , то потік  дуже близький до оптимуму. Тому метод ВП забезпечує від­шукання нерозгалужених потоків, що є доброю апроксимацією до оптимальних розгалужених потоків.
Розглянемо метод ВП для нерозгалужених потоків. Припустимо,   – початковий нерозгалужений потік. Візьмемо .
Обчислюємо матрицю  де ;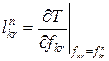
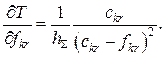
Знаходимо матрицю найкоротших шляхів  у мет­риці .
Припустимо, . Для кожної вимоги  виконуємо такі операції:
а) знаходимо потік , який виходить з   шляхом девіації потоку вимоги  по найкоротшому шляху , що задається матрицею П;
б) якщо  – допустимий потік і , то переходимо до наступного кроку, у протилежному випадку переходимо до кроку г);
в) беремо ;
г) якщо усі вимоги  переглянуті, то переходимо до наступного кроку, у іншому випадку повертаємося до кроку а).
4. Якщо , то роботу алгоритму закінчено. Метод ВП більше не може покращити нерозгалужений потік. Інакше вва­жаємо ,  і переходимо до кроку 1.
Даний алгоритм збігається за скінченне число кроків, тому що є лише кінцеве число нерозгалужених потоків, а повторення того самого потоку виключаються за умовами зупинки.
Розв’язання задачі розподілу потоків за невідомих пропускних здатностей каналів
Під час розв’язання задачі синтезу структури СД у ціло­му, відповідно до наведеної раніше постановки задачі, виникне необхідність вирішення таких окремих задач проектування, як синтез топології, РП, ВПЗ КЗ. У цьому випадку доводиться роз­в’язувати задачу РП на етапі, коли ПЗ КЗ ще не відомі, а ВПЗ КЗ здійснюється пізніше так, щоб забезпечити передачу заданих потоків у КЗ з максимальною якістю.
З цією метою був розроблений алгоритм визначення марш­рутів і розрахунку потоків у КЗ, який дозволяє забезпечити після оптимального ВПЗ КЗ мінімум часу затримки повідомлення в мережі. Розглянемо постановку задачі і метод її розв’язання.
Припустимо, є багатозв’язна СД, яка задана у вигляді неорієнтованого зваженого графа , де  – множина вершин графа, що відповідає множині вузлів мережі А;  – множина його ребер, вагу ребра  позначимо як . Припускатимемо, що при декількох маршрутах передачі інформації від вершини  до  вона завжди передається по шляху мінімальної вартості. Потрібно розрахувати параметри мережі : інформаційні потоки кожної з гілок і маршрути передачі інформації, при яких загальна вартість мережі буде мінімальною (структура мережі передбачається при цьому заданою).
Вихідні дані: топологія мережі задана матрицею суміжності  

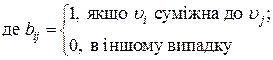
і матриця питомої вартості передачі одиниці інформації   між двома суміжними вузлами мережі.
У процесі роботи алгоритм використовує такі робочі мат­риці:  – матриця питомих вартостей передачі одиниці інформації з   до  по шляху мінімальної вартості;  – матриця мінімальних маршрутів на мережі , де елемент  – вершина, суміжна з , по шляху мінімальної вартості до ;  – шукана матриця інформаційних потоків мережі,  – сумарний трафік (потік), який передається по ребру , біт/с.
Розглянемо опис алгоритму. Алгоритм складається зі скінченної кількості однотипних ітерацій, у ході яких будують і уточнюють G, П, а потім знаходять F.
Як алгоритм для визначення найкоротших шляхів між усіма парами вузлів мережі використовуємо алгоритм, запропонований Флойдом. Кожному ребру  графа поставлена у відповідність його довжина або вага . Тоді довжиною шляху  буде сума ваг ребер, які його утворять. Потрібно знайти шляхи мінімальної довжини в графі між довільно взятою парою вершин  і .
Як початкове значення елементів візьмемо . Передба­чається, що усі величини  не є від’ємними. Якщо деяка пара вершин ,  не зв’язана дугою, то вважається . Величини  не обов’язково повинні відповідати нерівності трикутника . Якби ця нерівність виконувалася, задача виявилася б тривіальною, тому що тоді найкоротшим шляхом з  у була б завжди дуга . Величини , крім того, не обов’язково повинні відповідати умові симетрії .
Застосування алгоритму Флойда дозволяє визначити мат­рицю маршрутів, після чого необхідно визначити трафік у КЗ (матрицю F). Для цього використовується процедура «пропустити потік». Опишемо її.
Перед початком задамо   спочатку інфор­мація в мережі не передається.
Процедура складається зі скінченної кількості однотипних ітерацій, у яких знаходяться елементи .
Опишемо одну ітерацію.
Для заданих і і j знаходимо в матриці маршрутів П елемент  і беремо , для елемента матриці трафіку  виконуємо   
Якщо , то ітерація завершується. Інакше беремо
Знаходимо , беремо  і виконуємо .
Переходимо до кроку 2.
У результаті, виконавши цю процедуру для всіх пар вузлів мережі, ми визначимо потоки в каналах для знайденої множини мінімальних шляхів.
На етапі визначення мінімальних шляхів (маршрутних таблиць у вузлах) як вартість (або довжина) шляху між вузлами мережі брали   оцінки величини затримки. При цьому виникає складність у тому, як визначити дану величину, не вибравши попередньо ПЗ КЗ. Для цього розглянемо, які фактори, пов’язані зі структурою мережі, впливають на затримку.
Величина часу затримки повідомлення в мережі має такі складові: час передачі пакета в КЗ, час очікування пакета в черзі на передачу і час поширення електромагнітної енергії в ЛЗ. Таким чином, затримку передачі між кінцевими пунктами можна оцінити як

                                         

 

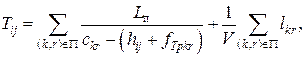
де V – швидкість поширення електромагнітної енергії в ЛЗ, м/с;
 – відстань між вузлами  і , м;
 – середня довжина пакета в мережі, біт;
 – сумарна інтенсивність потоків між суміжними вузлами  і , біт/с.
З аналізу виразу (12.22) можна помітити, що при невеликих значеннях ПЗ КЗ другим доданком можна знехтувати через його малість порівняно з першим, оскільки час затримки передачі набагато менше часу поширення сигналу в ЛЗ. Тоді затримка повідомлення в мережі залежить від кількості передач на шляху його проходження. Отже, як вартість шляху між вузлами ме­режі можна вибрати кількість передач. Тому матрицю вартості визначимо як

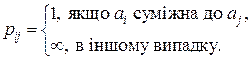
У випадку, коли ПЗ КЗ великі, час поширення сигналу в ЛЗ впливає на результуючу затримку пакета в мережі сильні­ше, ніж час передачі, і, отже, як вартість шляху між вузлами мережі слід взяти відстань між вузлами:

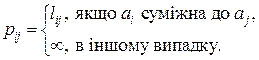
Вимогу щодо величини середньої затримки в мережі у цьому випадку буде виконано на етапі вибору пропускної здатнос­ті КЗ.

 

<-На зміст->