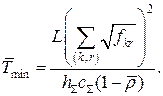<-На зміст->

 

12.3.3 Вибір пропускної здатності каналів

 

Розглянемо декілька підходів до вирішення проблеми вибору пропускних здатностей (ВПЗ) КЗ у транспортній мережі і використання різних критеріїв якості. Передбачається лі­нійна залежність вартості від ПЗ ЛЗ. При цьому збереження  загальної вартості мережі є постійно еквівалентним підтримці і загальній ПЗ мережі на фіксованому рівні. Використовуючи зазначене припущення, визначають оптимальний розподіл ЛЗ за критерієм мінімуму середнього часу затримки повідомлень. Такий підхід приводить до ВПЗ відповідно до так званої «стратегії квадратного кореня», при якій ПЗ кожної ЛЗ пропор­ційна квадратному кореню з величини інтенсивності трафіку, що проходить цією лінією. Далі цей підхід порівнюється з двома іншими стратегіями ВПЗ: стратегією рівномірного розподілу, за якою усі ЛЗ мають однакову ПЗ, і пропорційною стратегією, за якою ПЗ пропорційна інтенсивності трафіку, що проходить по ЛЗ.
Хоча в дійсності припущення щодо пропорційної залежності між вартістю і ПЗ не є справедливим (вартість залежить нелінійно від головних параметрів: ПЗ, типу орендованих ЛЗ і обслуговування, довжини ЛЗ і        т. д.), воно забезпечує повністю прийнятний у першому наближенні ВПЗ КЗ у мережі. Цей підхід дозволяє оцінити, якими мають бути ПЗ КЗ, щоб середній час затримки повідомлень був у заданому діапазоні значень, а також достатньо просто визначити вплив структури мережі і вибрати стратегію передачі повідомлень.
Можуть розглядатися й інші критерії якості. При цьому задача може формулюватися таким чином: вибрати ПЗ КЗ так, щоб мінімізувати найбільшу затримку, що може виникнути в мережі. Такий підхід веде до вирівнювання часових затримок. Якість обслуговування в цьому випадку однакова для користувачів, які створюють як велике, так і незначне навантаження.
Для розв’язання задачі розглянемо роботу КД, розташованого у вузлі мережі, який забезпечує прийом вхідних повідомлень і їх передавання у відповідний вихідний канал після необхідної буферизації й обробки. У найпростішій моделі передбачаєть­ся, що всі входи КД скануються фактично одночасно, так що кожне повідомлення, що з’явилося на вході, вводиться у від­повідну буферну пам’ять за принципом «першим прийшов – першим обслугований». Деталі операцій сканування і (або) обробки переривань при цьому опущено. Інші способи введення повідомлень у КД, включаючи опитування і випадковий доступ, ми не розглядаємо. Тип концентрації, що тут досліджується, часто називають статистичним або асинхронним ущільненням (мультиплексуванням). Після необхідної обробки повідомлення, що направляються в чергу до ЛЗ і виводяться по одному в цю лінію. При очікуванні на звільнення ЛЗ виникає певна часова затримка. Кількість вхідних ЛЗ у загальному випадку може бути довільною. Кожний концентратор має одну вихідну ЛЗ. Опустимо подробиці, пов’язані з концентрацією і буферизацією, тому що нас цікавить тільки ВПЗ КЗ. Не враховуватимемо також накладні витрати при передачі повідомлення, розбивку буферної пам’яті на блоки і т. д. До подальшого спрощення веде також припущення про те, що затримка, викликана обробкою повідомлень у вузлі, нехтовно мала порівняно з затримкою, викликаною очікуванням звільнення вихідної ЛЗ.
Розв’язання задачі при обмеженні на сумарну пропускну здатність каналів у мережі
Припустимо, що вхідний потік повідомлень – пуассонівський з інтенсивністю , довжина повідомлень підпорядкову­ється експоненційному закону розподілу із середнім значенням  біт (тобто довжина повідомлень у моделі не є дискретною величиною) і обсяг буферної пам’яті є необмеженим. Тоді для середнього часу затримки повідомлення (у секундах) у КЗ одер­жимо такий вираз:

                                                                     

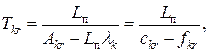
де  – ПЗ КЗ, біт/с;
 – вхідний потік повідомлень, біт/с.
Ця затримка містить середній час передачі повідомлення  і середній час очікування в черзі. Випадок обмеженого обсягу буферної пам’яті і більш реальні моделі трафіку тут не розглядаються. Припущення про необмеженість обсягу пам’яті відразу запобігає можливості блокування повідомлень, при ви­никненні якого повідомлення не можуть передаватися по КЗ (уся буферна пам’ять заповнена). Якщо обсяг буферної пам’яті настільки великий, що імовірність блокування менше , при­пущення про нескінченний обсяг буферної пам’яті при розра­хунку середнього часу затримки цілком прийнятне.
Вираз (12.23) показує, що при збільшенні  (інтенсивності трафіку) і наближенні до величини  час затримки необмежено зростає. Цей факт визначає верхню межу значень завантаження ЛЗ:

                                                                                       

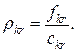
З урахуванням (12.24) вираз (12.23) перетвориться до вигляду

                             

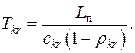
При  одержимо: , тобто величина затримки в цьому випадку збігається із середнім часом передачі повідомлення. При   стає дуже великим. Наприклад, якщо  пов./с і     біт, то при  біт/с середній час затримки при передачі по вихідній ЛЗ складає 2 с. При с – час, необхідний для передачі 120 біт по ЛЗ, що працює зі швидкістю 100 біт/с, і 0,8 с – середній час очікування в черзі.
Наша мета в тому, щоб мінімізувати середній час затримки в мережі, за умови, що загальна ПЗ КЗ фіксована. Припустимо,  – сумарний інформаційний потік, що надходить у мережу. Середня затримка повідомлень у мережі

                                                                           

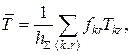
де підсумовування здійснюється по всіх ЛЗ мережі.
У формулі (12.26)  – середньозважена часова затримка, а  визначається рівнянням (12.23). Припускаючи, що загальна ПЗ     фіксована, знайдемо значення , що мінімізує . Розв’язання цієї задачі найбільш зручно виконувати за допо­могою методу множників Лагранжа. Можна показати, що по­шук мінімуму зводиться до мінімізації суми . Множник Лагранжа ( вибирається так, щоб .
Складемо функцію Лангранжа:

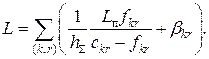
Прирівняємо до нуля окремі похідні :

.

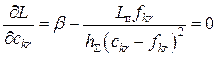З цього рівняння знайдемо :

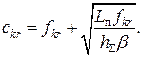
Після підстановки цього значення в рівність обмеження одержимо,

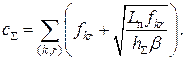
Звідси знаходимо

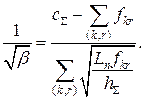
Отже,

                                                 
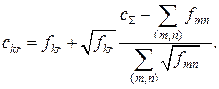
Цей вираз можна записати як

                                               
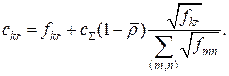
Тут  – величина завантаження всієї мережі, а константа  Вираз (12.28) можна використовувати в рівнянні (8.23) для визначення часових затримок , а з рівняння (8.26) випливає вираз для мінімальної середньої затримки повідомлень

                                 

Зазначений спосіб визначення  називають вибором ПЗ за принципом «квадратного кореня», тому що вираз для  містить член, пропорційний . Зазначимо, що мінімальний середній час затримки  обернено пропорційний ПЗ . Зазначена вище обернена залежність є прикладом обмінного співвідношення між двома величинами. Необхідність дослідження подібних співвід­ношень очевидна.
Під час аналізу мережі зі структурою типу «дерево» або розподіленої необхідно враховувати не тільки повідомлення від терміналів, підключених до вузлового концентратора, але і повідомлення, що надходять по КЗ з інших вузлів. В умовах статистичного ущільнення інтенсивності вхідних потоків повідомлень необхідно підсумовувати для того, щоб одержати інтенсивність загального вихідного потоку. Але статистичні характеристики повідомлень у послідовних КЗ пов’язані між собою (наприклад, часи затримок є взаємозалежними). У цьому випадку аналіз стає більш складним. Практика, однак, свідчить, що для більшості випадків залежністю послідовних затримок можна знехтувати. Це, зокрема, справедливо за умов малого трафіку, а також якщо зовнішніх повідомлень досить багато і для внутрішніх повідомлень, що надходять з інших вузлів, ця залежність виявляється незначною. Використовуватимемо так зване припущення про незалежність, яке базується на нехтуванні залежністю між чергами. Такий підхід можна виправдати тим, що нас цікавлять тільки наближені результати, тому що часто реальні статистичні дані про роботу мережі не відомі. Припущення про пуассонівський характер надходження повідомлень і експоненційний розподіл довжин повідомлень також є лише грубою апроксимацією реальних умов. У рамках зроблених припущень вважаємо, що повідомлення генеруються незалежно для кожного вузла, при чому довжини повідомлень незалежні й експоненційно розподілені. Інтенсивності всіх потоків, що надходять у вузол (зовнішніх і від інших вузлів), просто підсумовуємо, тому що відповідно до припущення потоки повідомлень, що надходять від інших вузлів, незалежні в сукупності.
Приклад. КД розташовано в кожному з 7-ми міст побудованої мережі передачі даних і з’єднано з центром вузлом. До КД підключені термінали зі швидкістю передачі 14,4 кбіт/с, середня довжина повідомлення L = 1540 біт, кожний термінал передає в середньому одне повідомлення за Т = 12 с.
Розподіл терміналів по містах такий:
Донецьк ­– 222;
Житомир – 320;
Запоріжжя – 346;
Івано-Франківськ – 240;
Київ – 345;
Кіровоград – 355;
Луганськ –276.
Необхідно визначити:
- мінімальний середній час затримки для мережі, якщо загальна ПЗ     =256 кбіт/с і = 768 кбіт/с, враховувати час затримки тільки в напрямку до центрального вузла;
- оптимальне значення ПЗ кожної ЛЗ, що з’єднує з центральним вузлом, при двох значеннях загальної ПЗ відповідно до стратегії «квадратного кореня».
У мережі можуть використовуватись КЗ з ПЗ 64, 128, 256 кбіт/с. Провести ВПЗ КЗ для мережі із заданого набору таким чином, щоб ПЗ цих КЗ були близькі до ПЗ, знайдених у п. 2, а загальна ПЗ була близькою до  і . Порівняти отри­мане в даному випадку значення середнього часу затримки з мінімально можливим.
Розглянути рівномірну і пропорційну стратегії розподілу загальної ПЗ мережі при  між ЛЗ, для кожної стратегії ви­значити середній час затримки – окремо для кожної ЛЗ і для мережі в цілому. Порівняти з аналогічним результатом у п.1.
Задача ВПЗ вимагає розподілу внутрішнього трафіку мережі, для розрахунку якого необхідно знати всі маршрути в мережі до центрального вузла. Оскільки наша мережа є деревоподібною, то з будь-якого КД існує тільки один маршрут до центрального вузла. Припустимо, як центральний вузол виступає вузол № 5 (Київ), тоді маршрути:

 

з 1 у 5:

1-3-6-5;

з 2 у 5:

2-5;

з 3 у 5:

3-6-5;

з 4 у 5:

4-2-5;

з 6 у 5:

6-5;

з 7 у 5:

7-1-3-6-5.

Інтенсивність навантаження від і-го КД де  – кількість терміналів, підключених до і-го КД;  пов./с – інтенсивність потоку, що генерується одним терміналом.
Одержуємо:
= 18,5 пов./с,
 = 26,7 пов./с,
= 28,8 пов./с,
 = 20,0 пов./с,
 = 29,6 пов./с,
 = 23,0 пов./с.
Загальний трафік дорівнює 146,6 пов./с або 225,8 кбіт/с. Зовнішній трафік мережі показано на рис. 12.3. Під час аналізу мережі зі структурою типу «дерево» необхідно враховувати не тільки повідомлення від терміналів, підключених до вузлового концентратора, але і повідомлення, що надходять по КЗ з іншого вузла. Інтенсивності всіх потоків, що надходять у вузол (зовнішніх і від інших вузлів), просто додаються, тому що відповідно до припущення потоки повідомлень, які надходять від інших вузлів, незалежні в сукупності. У результаті маємо внутрішній трафік:  = 20 пов./с;  = 16,7 пов./с;   = 99,9 пов./с;  = 70,3 пов./с;  = 41,4 пов./с;  = 22,9 пов./с, де  – інтенсивність навантаження в і-й ЛЗ. Інформаційні потоки, що передаються по КЗ, відповідно дорів­нюють:  = 30,8 кбіт/с;  = 71,9 кбіт/с; = 153,9 кбіт/с;  = 108,3 кбіт/с;            = 63,8 кбіт/с;  = 35,3 кбіт/с. Мінімальний середній час затримки повідомлень

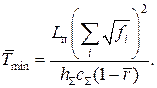
Одержуємо  = 256 кбіт/с, завантаження мережі  = 1,82; при                = 768 кбіт/с  = 0,61. Оскільки величина завантаження мережі не може перевищувати значення 1, то можна зробити висновок, що при загальній ПЗ  = 256 кбіт/с мережа не може забезпечити передачу заданих обсягів інформації. Тому  = 1 Мбіт/с.


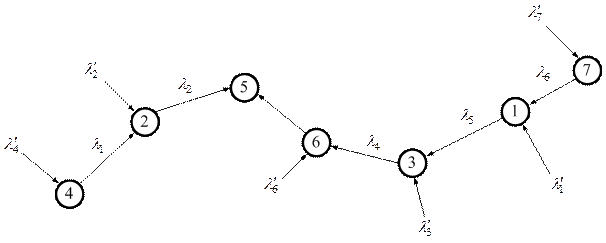
Рисунок 12.3 – Вихідні дані до задачі

Одержуємо при  = 1 Мбіт/с  = 31,2 мс, при  = 768 кбіт/с                = 57,8 мс.
Оптимальне значення ПЗ і-ї ЛЗ відповідно до стратегії «квадратного кореня» визначається з виразу

                                                               

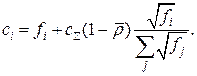
Середній час затримки повідомлення для кожної ЛЗ 

                                                                                    

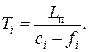
Результати розрахунків значень ПЗ наведені в таблицях 12.1 (для             = 1 Мбіт/с) та 12.2 ( = 768 кбіт/с).

 

 

 

Таблиця 12.1 - Результати розрахунків для  = 1 Мбіт/с

і

Оптимальний розподіл

Дискретний розподіл

Рівномірний розподіл

Пропорційний розподіл

, мс

, мс

, мс

, мс

1

30,8

92,35

25,02

64

46,39

170,67

11,01

67,76

41,67

2

771,9

165,94

16,38

128

27,45

170,67

15,59

158,18

17,34

3

153,9

291,48

11,19

256

15,08

170,67

91,83

338,58

8,34

4

108,3

223,71

13,34

256

10,43

170,67

24,69

238,26

11,85

5

63,8

152,38

17,39

128

23,99

170,67

14,41

140,36

20,11

6

35,3

101,19

23,37

128

16,61

170,67

11,38

77,66

36,36

 

 

= =1024

 = =31,2

= 960

=39,7

=
=1024

= 86,7

=1024

=34,1

 

         Таблиця 12.2 - Результати розрахунків для  = 768 кбіт/с

і

 

 

Оптимальний розподіл

Дискретний розподіл

Рівномірний розподіл

Пропорційний розподіл

, мс

, мс

, мс

, мс

1

30,8

64,03

46,34

64

46,39

128

15,84

51,13

75,76

2

71,9

122,67

30,33

128

27,45

128

27,45

119,35

32,45

3

153,9

228,18

20,73

256

15,08

128

255,47

15,16

4

108.3

170,62

24,71

128

78,17

128

78,17

179,78

21,55

5

63,8

111,63

32,20

128

23,99

128

23,99

105,91

36,57

6

35,3

70,88

43,29

64

53,66

128

16,61

58,60

66,10

 

 

=768

 = 58,7

=768

=78,7

=
=768

=

=768

=62,0

Виберемо значення ПЗ КЗ з набору 64, 128, 256 кбіт/с і розрахуємо середні часи затримок. Середня затримка повідомлень у мережі визначається з виразу

                                                                                

Результати наведені в табл. 12.1 та 12.2. Як видно з таблиць, значення збільшилися.
Розглянемо ще дві стратегії розподілу ПЗ КЗ, такі як стратегія рівномірного розподілу і стратегія пропорційного розпо­ділу.
1. Стратегія рівномірного розподілу, за якої загальна ПЗ  розподіляється однаково між усіма ЛЗ незалежно від інтенсивності трафіку, що проходить по кожній з цих ліній. У цьому випадку ПЗ кожної ЛЗ

2. Стратегія пропорційного розподілу, за якою с пропорційне
заданому значенню потоку , тобто

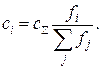
Середній час затримки повідомлень у ЛЗ обчислюється за формулою (12.31), а середній час затримки в мережі – за (12.32). Результати обчислення наведені в табл. 12.1 та 12.2, з аналізу даних яких можна зробити кілька зауважень.
При мінімізації середнього часу затримки слабко наван­таженим ЛЗ відповідає менше значення ПЗ, ніж сильно на­вантаженим. Порівняйте, наприклад, ПЗ ЛЗ 1 і 6 із ПЗ ЛЗ 3 (табл. 12.2). Тому час затримки слабко завантажених ЛЗ наба­гато вище, ніж сильно завантажених. Для ЛЗ 1 при виборі за правилом «квадратного кореня» середній час затримки дорівнює 16,34 мс, у той час як для ЛЗ 3 – тільки 20,73 мс. Таким чином користувач, що генерує слабкий потік, штрафується на користь користувачів зі значним трафіком. Наприкінці даного розділу стисло розглядається інший критерій, за якого штрафи відсутні і час затримки для всіх ЛЗ однаковий.
Правило пропорційного ВПЗ ще більше підсилює розхо­дження між слабко і сильно навантаженими ЛЗ. Нерівність між ПЗ більша, ніж при виборі за правилом «квадратного кореня», при одночасному збільшенні часу затримки.
3. Правило рівномірного розподілу хоча і веде до збільшен­ня загального середнього часу затримки, але зменшує різницю в часі затримки для слабко і сильно завантажених ЛЗ. Хоча для даного прикладу можемо спостерігати обернену картину, коли час затримки повідомлення для сильно навантаженої ЛЗ значно більший за час затримки для слабко навантаженої ЛЗ або навіть не може забезпечити передачу трафіку через КЗ. Останнє пов’язано з тим, що в даному випадку обране недостатнє зна­чення сумарної ПЗ КЗ.
Вище була розглянута задача ВПЗ КЗ для простої мережі, в якій термінали семи міст передають повідомлення вузлу, що знаходиться в центрі мережі. У загальному випадку повідо­млення можуть циркулювати між різними вузлами мережі. Це приводить до необхідності розглянути мережі розподіленої структури. Стратегії ВПЗ КЗ мереж цього типу ідентичні до тих, що вже обговорювалися для мережі з простою конфігурацією, якщо знову застосувати припущення про незалежність, роз­глянуте в попередньому розділі.
Для ВПЗ КЗ у розподіленій мережі необхідно знати величину й інтенсивність трафіку, переданого між містами, і маршрути повідомлень, що надходять у мережу в одному місті і прямують в інше.
При ВПЗ кожної з ЛЗ використовуватимемо введене раніше припущення про незалежність: повідомлення, що підлягають передачі по кожній з ЛЗ мережі, статистично не залежать від повідомлень, які з’являються в інших вузлах мережі. Необхідно також визначити інтенсивності потоків повідомлень, що про­ходять по кожній ЛЗ.
ВПЗ ЛЗ (біт/с) залежить не тільки від інтенсивності потоків повідомлень, але також і від довжин повідомлень. Нагадаємо, що відповідно до виразу (12.23) середній час затримки для ЛЗ  через очікування в черзі і витрати часу на передачу

                                                                                

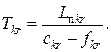
Для отримання формули (12.33) використовувалося припущення про пуассонівский характер потоку, експоненційний розподіл до­вжини повідомлення і наявності буферної пам’яті необмеженого обсягу. Оскільки повідомлення надходять від різних джерел і вузлів, природно виникає питання про величину середньої довжини повідомлень . Припустимо, що для всіх ЛЗ мережі повідомлення мають однакову середню довжину . Це спростить нам розв’язання задачі. У більш складних випадках певних ЛЗ можуть передаватися повідомлення різних типів. Згадаємо приклади мереж, у яких кілька типів повідомлень різної довжини передавалося в одному напрямку по будь-якій ЛЗ. Це були повідомлення різних категорій: керувальні або інформаційні повідомлення; повідомлення АСК, якщо квитанція не включалася в інформаційні повідомлення, і т. д. У цьому випадку необхідно визначити середнє значення довжини повідомлення. Наприклад, це можна зробити так:

Підсумовування проводиться за всіма повідомленнями, що із джерела   направляються в пункт призначення  по ЛЗ .
У загальному випадку необхідно враховувати різницю в дов­жинах повідомлень, переданих у протилежних напрямках. ПЗ дуплексних ЛЗ слід вибирати, беручи до уваги найбільш завантажений напрямок передачі.
Знаючи величину потоку повідомлень по ЛЗ   і серед­ню довжину повідомлення , можна тепер визначити вплив ВПЗ ЛЗ на величину часу затримки. Оптимальні значення ПЗ КЗ, для яких середній час затримки в мережі мінімальний, знаходи­мо так само, як у випадку простої структури мережі (нескладні розрахунки показують, що в припущені незалежності статистичних характеристик повідомлень від лінії до лінії аналіз, проведений раніше, справедливий і в даному випадку). Таким чином оптимальна ПЗ КЗ визначається з виразу (12.28):

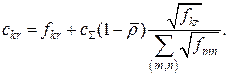
Нагадаємо, що  – фіксована загальна ПЗ мережі, а  Середній час затримки повідомлення в мережі визначається з виразу (12.26):

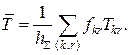
Мінімальний середній час затримки знаходимо з виразу (12.22):

 

<-На зміст->