<-На зміст->
12.4 Синтез структури однорангової системи доступу
Одноранговою системою доступу називається система, в якій усі вузли мережі рівноправні. Задача синтезу однорангової СД виникає, коли в мережу необхідно об’єднати множину рівнозначних вузлів або під час проектування магістрального сегмента СД. Відповідно до загальної постановки задачі синтезу структури СД, цей випадок можна розглядати як варіант, коли ![]() і
і ![]() тобто ВД необхідно установити у всіх вузлах мережі.
тобто ВД необхідно установити у всіх вузлах мережі.
Розглянемо постановку і математичну модель задачі визначення оптимальних параметрів телекомунікаційних засобів і синтезу оптимальної структури ТКС відповідно до критерію «мінімум вартості».
Задано такі вихідні дані: множина ![]() які задані своїми координатами
які задані своїми координатами ![]() ; матриця вимог у передачі
; матриця вимог у передачі ![]() ; матриця вартості будівництва ЛЗ
; матриця вартості будівництва ЛЗ ![]() ; величина витрат
; величина витрат ![]() на організацію
на організацію
КЗ заданої ПЗ; коефіцієнт зв’язності ![]() ; припустима величина середньомережевої затримки повідомлення в мережі
; припустима величина середньомережевої затримки повідомлення в мережі ![]() .
.
Введемо такі змінні:
![]() – середня довжина повідомлення;
– середня довжина повідомлення;
![]() – ПЗ КЗ між пунктами
– ПЗ КЗ між пунктами ![]() і
і ![]() , біт/с;
, біт/с;
Топологію мережі задамо матрицею суміжності ![]() , де
, де 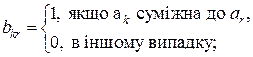
![]() – сумарний трафік (потік), переданий по КЗ
– сумарний трафік (потік), переданий по КЗ ![]() , біт/с.
, біт/с.
Необхідно знайти таку структуру мережі заданої зв’язності ![]() і ПЗ всіх КЗ
і ПЗ всіх КЗ ![]() , при яких забезпечується передача заданих графіків між будь-якою парою вузлів
, при яких забезпечується передача заданих графіків між будь-якою парою вузлів ![]() –
– ![]() із середньою затримкою
із середньою затримкою ![]() , що не перевищує припустиму
, що не перевищує припустиму ![]() . Наведені витрати на організацію мережі при цьому мають бути мінімальними.
. Наведені витрати на організацію мережі при цьому мають бути мінімальними.
Математична модель задачі має такий вигляд:
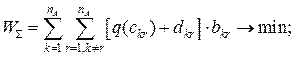
![]()
![]()
Для розв’язання даної задачі існують методи оптимізації, такі як метод НП, метод усунення гілок і метод заміни гілок, але вони мають загальний недолік: у них не запропонований метод синтезу початкової структури і визначення параметрів структурних елементів, який відповідає всім обмеженням, що сильно затягує пошук розв’язку. Нижче розглядається модифікований метод синтезу, що базується на методі М-структур.
У методі М-структур початкова структура заданої зв’язності (![]() ) вибирається не випадково, а генерується цілеспрямовано за допомогою спеціального алгоритму. В основі розробленого алгоритму лежать такі ідеї: спочатку на множині усіх вузлів будують НЗД, що далі перетвориться в надлишкову структуру заданої зв’язності
) вибирається не випадково, а генерується цілеспрямовано за допомогою спеціального алгоритму. В основі розробленого алгоритму лежать такі ідеї: спочатку на множині усіх вузлів будують НЗД, що далі перетвориться в надлишкову структуру заданої зв’язності ![]() . Далі оптимізують початкову структуру
. Далі оптимізують початкову структуру ![]() за критерієм мінімуму вартості при виконанні усіх введених обмежень.
за критерієм мінімуму вартості при виконанні усіх введених обмежень.
У базовому варіанті даного алгоритму на стадії доведення початкової структури СД, що являє собою НЗД, до необхідної величини зв’язності, пропонувалося побудувати цикл мінімальної довжини, що проходить через висячі вершини графа, еквівалентного мережі. Для цього застосовувався алгоритм розв’язанння задачі комівояжера, що потребувало великих часових витрат, оскільки складність розв’язання задачі комівояжера пропорційна факторіалу від кількості висячих вершин.
У результаті проведеного аналізу даного алгоритму було визначено, що використання циклу мінімальної довжини для доведення зв’язності структури СД до необхідного значення є недоцільним. Цей висновок базується на такому: для того щоб одержати з однозв’язної структури двозв’язану, достатньо з’єднати між собою усі висячі вершини графа. Таким чином, суть розв’язуваної підзадачі зводиться до того, що необхідно знайти множину ребер графа, яка з’єднує між собою підмножину висячих вершин вихідного графа так, щоб сумарна довжини ребер, що додатково вводяться, була мінімальною. У випадку використання циклу мінімальної довжини сумарна довжина ребер, що знову вводяться, не досягає свого мінімального значення. Менше значення можна одержати, використовуючи для з’єднання висячих вершин графа НЗД, тому що для зваженого графа справедливими є такі твердження:
- мінімальна довжина гамільтонового ланцюга менше гамільтонового циклу мінімальної довжини;
- сумарна довжина НЗД менше мінімальної довжини гамільтонового ланцюга, тобто
![]()
де ![]() – сумарна довжина НЗД;
– сумарна довжина НЗД;
![]() – мінімальна довжина гамільтонового ланцюга;
– мінімальна довжина гамільтонового ланцюга;
![]() – мінімальна довжина гамільтонового циклу.
– мінімальна довжина гамільтонового циклу.
Суть модифікації методу М-структур в тому, що на стадії доведення початкової структури СД до необхідної величини зв’язності виконується заміна процедури знаходження циклу мінімальної довжини на процедуру знаходження НЗД, що з’єднує висячі вершини. Складність алгоритму розв’язання в останньому випадку пропорційна квадрату кількості висячих вершин графа.
Розглянемо опис алгоритму. Припустимо, задана множина АС А і матриця вимог ![]() .
.
1. Будуємо НЗД ![]() . Для цього використовується алгоритм
. Для цього використовується алгоритм
синтезу деревоподібних структур, що з’єднує усі вузли мережі,
наприклад, алгоритм Краскаля.
Отримана структура ![]() є однозв’язною, тому що інакше вона мала б цикли і, отже, не була б деревом. У той же час, за умовами надійності потрібно, щоб вона була k-зв’язною і не мала висячих вершин і ребер зчленування. Тому переходимо до кроку 2.
є однозв’язною, тому що інакше вона мала б цикли і, отже, не була б деревом. У той же час, за умовами надійності потрібно, щоб вона була k-зв’язною і не мала висячих вершин і ребер зчленування. Тому переходимо до кроку 2.
2. Визначаємо всі кінцеві вершини графа. Для цього позначимо усі вузли, що мають зв’язок тільки з одним іншим вузлом у мережі, тобто ступінь відповідної вершини графа дорівнює одиниці. В останньому випадку в матриці суміжності в рядку, що відповідає даному вузлу, є тільки один ненульовий елемент. Позначимо ці вузли через ![]() . Будуємо НЗД, що з’єднує всі кінцеві вершини графа
. Будуємо НЗД, що з’єднує всі кінцеві вершини графа ![]() , й одержуємо структуру
, й одержуємо структуру ![]() , для якої виконується умова зв’язності
, для якої виконується умова зв’язності ![]() .
.
Якщо за умовою задачі потрібна організація мережі з ![]() , то ми повторюємо крок 2, підвищуючи на кожній ітерації зв’язність мережі на одиницю, поки не одержимо структуру з необхідним
, то ми повторюємо крок 2, підвищуючи на кожній ітерації зв’язність мережі на одиницю, поки не одержимо структуру з необхідним ![]() . Для розв’язання цієї підзадачі позначаємо вершини графа зі ступенем, меншим ніж величина
. Для розв’язання цієї підзадачі позначаємо вершини графа зі ступенем, меншим ніж величина ![]() , яку ми хочемо одержати на даному кроці.
, яку ми хочемо одержати на даному кроці.
Після проведення процедури підвищення зв’язності мережі ми одержимо структуру, що має надлишкові ребра, вилучення яких не зменшує коефіцієнт зв’язності.
Для структури ![]() розв’язуємо задачу РП і ВПЗ КЗ.
розв’язуємо задачу РП і ВПЗ КЗ.
Підзадача РП визначає найкоротші шляхи між усіма вузлами мережі, а також дозволяє розрахувати потоки по всіх гілках.
У результаті застосування процедур РП і ВПЗ знаходимо такі потоки в гілках ![]() і ПЗ
і ПЗ ![]() для усіх
для усіх ![]() , для яких досягається
, для яких досягається
![]()
за умови
![]()
Знайдене розв’язання є оптимальним лише для деякої фіксованої структури ![]() , тому переходимо до блоку оптимізації.
, тому переходимо до блоку оптимізації.
Блок оптимізації. Припустимо, задана початкова структура ![]() у вигляді k-зв’язного графа і визначені ПС КЗ
у вигляді k-зв’язного графа і визначені ПС КЗ ![]() , при яких справедливі вирази (12.35) і (12.37).
, при яких справедливі вирази (12.35) і (12.37).
Метою блоку оптимізації є спрямований пошук раціональної структури ![]() , що забезпечує мінімум критерію вартості
, що забезпечує мінімум критерію вартості ![]() . Блок оптимізації містить однотипні ітерації, на кожній з яких виконуються локальні перетворення поточної структури
. Блок оптимізації містить однотипні ітерації, на кожній з яких виконуються локальні перетворення поточної структури ![]() , перераховуються всі її характеристики і визначається нова величина критерію
, перераховуються всі її характеристики і визначається нова величина критерію ![]() . Опишемо першу ітерацію.
. Опишемо першу ітерацію.
3. Вибираємо величину k, в якій ступінь ![]()
Вибираємо у вершині k ребро ![]() .
.
Перевіряємо можливість вилучення ребра ![]() , тобто виконання заданих умов зв’язності, зокрема відсутність точок зчленування і ребер зчленування після вилучення ребра
, тобто виконання заданих умов зв’язності, зокрема відсутність точок зчленування і ребер зчленування після вилучення ребра ![]() . Якщо ці умови виконуються, то переходимо до кроку 4, у іншому випадку повертаємося до кроку 2 і вибираємо іншу гілку
. Якщо ці умови виконуються, то переходимо до кроку 4, у іншому випадку повертаємося до кроку 2 і вибираємо іншу гілку ![]() для аналізу.
для аналізу.
4. Виконуємо процедуру «вилучення ребра» ![]() із графа
із графа ![]() й одержуємо новий граф
й одержуємо новий граф ![]() .
.
Перераховуємо всі трафіки в мережі ![]() за допомогою процедури РП і знаходимо скореговані значення трафіків усіх гілок.
за допомогою процедури РП і знаходимо скореговані значення трафіків усіх гілок.
Звертаємося до процедури ВПЗ і визначаємо оптимальні ПЗ усіх КЗ ![]() (1), що забезпечують передачу потоків
(1), що забезпечують передачу потоків ![]() (1) під час виконання умов (12.35) і (12.37).
(1) під час виконання умов (12.35) і (12.37).
Знаходимо вартість мережі зі структурою ![]() :
:
![]()
Перевіряємо умову ![]()
Якщо умова виконується, то беремо ![]() і закінчуємо
і закінчуємо
ітерацію. У іншому випадку відновлюємо вилучене ребро
![]() і переходимо до кроку 2, вибравши для аналізу нове надлишкове ребро.
і переходимо до кроку 2, вибравши для аналізу нове надлишкове ребро.
При цьому на кожній ітерації ми вилучаємо зі структури ![]() ребро, що приводить до зменшення критерію
ребро, що приводить до зменшення критерію ![]() , не порушуючи умови зв’язності. Алгоритм продовжуємо виконувати доти, доки всі надлишкові ребра не будуть перевірені і вилучення кожного з них не приведе до покращення
, не порушуючи умови зв’язності. Алгоритм продовжуємо виконувати доти, доки всі надлишкові ребра не будуть перевірені і вилучення кожного з них не приведе до покращення ![]() . У цьому випадку структура
. У цьому випадку структура ![]() не може бути поліпшеною, завершується робота алгоритму. Закінчення алгоритму і його збіжність визначаються закінченням множини надлишкових ребер, які можна вилучити з мережі.
не може бути поліпшеною, завершується робота алгоритму. Закінчення алгоритму і його збіжність визначаються закінченням множини надлишкових ребер, які можна вилучити з мережі.