 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ЛАБОРАТОРНА РОБОТА №3 СТАНДАРТНА ТРАНСПОРТНА ЗАДАЧА
Придбання навичок побудови математичних моделей стандартних транспортних
задач ЛП і розв’язування їх у Microsoft Excel. Порядок виконання роботи 1. Відповідно до номера свого варіанта
виберіть умову задачі. 2. Побудуйте модель задачі, включаючи
транспортну таблицю. 3. Знайдіть оптимальний розв’язок
задачі в Excel і продемонструйте його викладачу. 4. Оформіть звіт з лабораторної роботи,
що повинен містити: - титульний аркуш; - транспортну таблицю, модель задачі з
вказанням всіх одиниць вимірювання; - результати розв’язування
задачі з вказанням одиниць вимірювання.
3.1 Теоретична частина
3.1.1 Стандартна модель
транспортної задачі
(ТЗ)
Задача про розміщення (транспортна задача) – це РЗ, у якій роботи і ресурси виміряються в тих самих одиницях. У таких задачах ресурси можуть бути розділені між роботами, і окремі роботи можуть бути виконані за допомогою різних комбінацій ресурсів. Прикладом типової транспортної задачі є розподіл (транспортування) продукції, що знаходиться на складах, на підприємствах-споживачах. Стандартна ТЗ визначається як задача
розроблення найбільш економічного плану перевезення продукції одного виду
з декількох пунктів відправлення в пункти призначення. При цьому величина
транспортних витрат прямо пропорційна обсягові перевезеної продукції і
задається за допомогою тарифів на перевезення одиниці продукції. Вихідні параметри моделі ТЗ: n – кількість пунктів відправлення, m – кількість пунктів призначення. а) б) [од. тов.]; в) Шукані
параметри моделі ТЗ 1. 2. Етапи побудови моделі 1. Визначення змінних. 2. Перевірка
збалансованості задачі. 3. Побудова
збалансованої транспортної матриці. 4. Задання ЦФ. 5. Задання обмежень. Транспортна модель
Цільова функція являє собою транспортні витрати на
здійснення всіх перевезень у цілому. Перша група обмежень указує, що запас
продукції в будь-якому пункті відправлення повинен дорівнювати сумарному обсягу
перевезень продукції з цього пункту. Друга група обмежень указує, що сумарні
перевезення продукції в деякий пункт споживання повинні цілком задовольнити
попит на продукцію в цьому пункті. Наочною формою подання моделі ТЗ є
транспортна матриця (табл. 3.1). З моделі (3.1) випливає, що сума запасів продукції у всіх пунктах відправлення повинна дорівнювати сумарній потребі у всіх пунктах споживання, тобто
Таблиця 3.1 – Загальний вигляд
транспортної матриці
Якщо (3.2) виконується, то ТЗ
називається збалансованою, у протилежному випадку – незбалансованою. Оскільки
обмеження моделі (3.1) можуть бути виконані тільки при збалансованій ТЗ, то при
побудові транспортної моделі необхідно перевіряти умову балансу (3.2). У
випадку, коли сумарні запаси перевищують сумарні потреби, необхідний додатковий
фіктивний пункт споживання, що буде формально споживати існуючий надлишок
запасів, тобто
Якщо сумарні потреби перевищують
сумарні запаси, то необхідно додатковий фіктивний пункт відправлення, що
формально заповнює існуючий недолік продукції в пунктах відправлення:
Уведення фіктивного споживача або
відправника спричинить необхідність формального задання фіктивних тарифів
На практиці можливі ситуації, коли у
визначених напрямках перевезення продукції неможливі, наприклад, через ремонт
транспортних магістралей. Такі ситуації моделюються за допомогою введення так
званих заборонних тарифів
3.2 Постановка
задачі
На складах зберігається борошно, яке
необхідно завезти в хлібопекарні. Номери складів і номери хлібопекарень
вибираються відповідно до варіантів табл. 3.4. Поточні тарифи перевезення
борошна [грн./т], щомісячні запаси борошна [т/міс.] на складах і потреби
хлібопекарень у борошні [т/міс.] зазначені в табл. 3.5. При цьому необхідно враховувати, що
через ремонтні роботи тимчасово немає можливості перевозити борошно з деяких
складів у деякі хлібопекарні. У табл. 3.4 це показано в графі “Заборона перевезення”. Наприклад, “2×3” означає, що не можна перевозити борошно зі складу
№2 у хлібопекарню №3. Крім того, необхідно врахувати, що
деякі хлібопекарні мають договори на гарантоване постачання борошна з певних
складів. У табл. 3.4 це показано в графі “Гарантоване постачання” у вигляді: номер складу помножити на номер хлібопекарні
дорівнює обсягу постачання. Наприклад, “1×4 = 3.3 Інстукція до виконання лабораторної роботи
Розв’язок задачі
полягає в необхідності організувати
оптимальні за транспортними витратами перевезення борошна з двох складів у три
хлібопекарні. Щомісячні запаси борошна на складах рівні 79,515 і 101,925 т, а щомісячні потреби хлібопекарень
складають 68,5, 29,5 і 117,4 т, відповідно. Борошно на складах зберігається і
транспортується в мішках по Таблиця 3.2 – Транспортні витрати з доставки борошна
(грн./т)
ТЗ являє
собою задачу ЛП, яку можна розв’язувати
симплекс-методом, що і відбувається при розв’язуванні таких задач у Excel. У
той же час існує більш ефективний обчислювальний метод – метод потенціалів, у випадку
застосування якого використовується специфічна структура умов ТЗ (3.1) і,
власне кажучи, відтворюються кроки симплекс-алгоритму. Виходячи з цього, у
лабораторній роботі необхідно побудувати модель задачі вигляду (3.1), придатну
для її розв’язування методом потенціалів. Визначення змінних. Позначимо через Перевірка збалансованості задачі. Перш ніж
перевіряти збалансованість задачі, треба виключити обсяг гарантованого
постачання з подальшого розгляду. Для цього віднімемо 4,5 т з таких величин: – із запасу першого
складу – з потреби в
борошні другої хлібопекарні
Відповідно до умови задачі борошно зберігається і перевозиться в мішках
по Для даної ТЗ має місце
співвідношення
Щомісячний сумарний
запас борошна на складах менший сумарної потреби хлібопекарень на 4677 – 3932 =
745 мішків борошна, звідси випливає висновок: ТЗ незбалансована. Побудова збалансованої транспортної матриці. Збалансована
транспортна матриця подана в таблиці 3.3. Вартість перевезення борошна повинна
бути віднесена до одиниці продукції, тобто до 1 мішка борошна. Так, наприклад,
тариф перевезення з першого складу в третій магазин дорівнює 420 грн./т · 0,045
т/міш. = 18,90 грн./міш. Таблиця
3.3 – Транспортна матриця задачі
Для встановлення балансу необхідний
додатковий фіктивний склад, тобто додатковий рядок у транспортній таблиці
задачі. Фіктивні тарифи перевезення задамо таким чином, щоб вони були дорожчі
реальних тарифів, наприклад, Неможливість доставки вантажів із
другого складу в третю хлібопекарню задається в моделі за допомогою тарифу, що
забороняє, що повинен перевищувати величину фіктивного тарифу, наприклад, Задання ЦФ Формальна ЦФ, тобто сумарні витрати на всі можливі
перевезення борошна, що враховуються в моделі, задається таким виразом:
При цьому варто враховувати, що унаслідок
використання фіктивних тарифів реальна ЦФ (тобто кошти, що у дійсності
прийдеться заплатити за транспортування борошна) буде менша формальної ЦФ (3.5)
на вартість знайдених у процесі розв’язування фіктивних перевезень. Задання обмежень
3.4 ВаріантиТаблиця
3.4 – Номери складів, хлібопекарень, заборонені і гарантовані постачання
Таблиця 3.5 – Запаси, потреби і тарифи перевезень
3.5 Запитання на захист роботи1. Що таке задача про розміщення? 2. Запишіть математичну модель транспортної задачі. 3. Перелічіть вихідні і шукані параметри моделі транспортної
задачі. 4. Яка суть кожного з етапів побудови моделі транспортної
задачі? 5. Розкрийте поняття збалансованості транспортної
задачі. 6. Що таке фіктивні і заборонні тарифи? 7. У якому співвідношенні повинні знаходитися
величини фіктивних і заборонних тарифів при необхідності їх одночасного
використання в транспортній моделі? 8. В чому суть транспортної задачі? 9. Яке
практичне значення транспортної задачі? 10.
Навіщо при розв’язуванні транспортної
задачі додаються фіктивні споживачі або постачальники? 11.
Що таке формальна цільова функція? 12.
Опишіть вхідні параметри транспортної задачі. 13.
Назвіть приклад використання транспортної
задачі. 14.
Яке значення в транспортної задачі мають
заборонні тарифи? 15.
Які фактори впливають на вартість фіктивних перевезень? 16.
У чому суть методу потенціалів при розв’язуванні
транспортної задачі? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Назад Зміст Далі | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
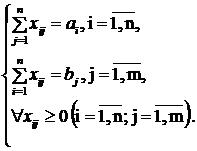
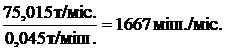 , а потреба першої хлібопекарні складає
, а потреба першої хлібопекарні складає 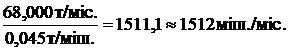
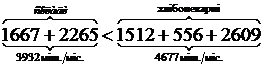 .
.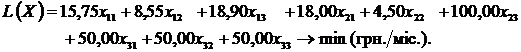
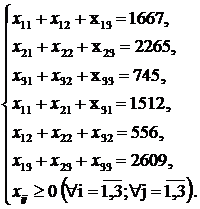 (міш./міс.)
(міш./міс.)