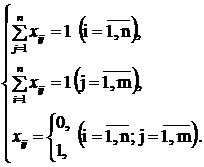Мета роботи

Придбання навичок побудови математичних моделей задач про призначення і розв’язування цих задач у Microsoft Excel.

Порядок виконання роботи

1. Відповідно до номера свого варіанта виберіть умову задачі.

2. Побудуйте модель задачі, включаючи транспортну таблицю.

3. Знайдіть оптимальний розв’язок задачі за допомогою Excel і покажіть його викладачу.

4. Оформіть звіт з лабораторної роботи, що повинен містити:

– титульний аркуш.

– транспортну таблицю і модель задачі з вказанням всіх одиниць вимірювання;

– результат розв’язування задачі з вказанням одиниць вимірювання.

4.1 Теоретична частина

Задача про призначення – це РЗ, у якій для виконання кожної роботи потрібно один і тільки один ресурс (одна людина, одна автомашина і т.д.), а кожен ресурс може бути використаний на одній і тільки одній роботі.

Таким чином, задача про призначення є окремим випадком ТЗ. Задача про призначення має місце при призначенні людей на посади або роботи, автомашин на маршрути, водіїв на машини, при розподілі груп по аудиторіях, наукових тим по науково-дослідних лабораторіях і т.п.

Вихідні параметри моделі задачі про призначення.

1. n – кількість ресурсів, m – кількість робіт.

2.  – одинична кількість ресурсу  (), наприклад: один працівник; один транспортний засіб; одна наукова тема і т.д.

3.  – одинична кількість роботи  (), наприклад: одна посада; один маршрут; одна лабораторія.

4.  – характеристика якості виконання роботи  за допомогою ресурсу . Наприклад, компетентність i-го працівника при роботі на j-й посаді; час, за який i-ий транспортний засіб перевезе вантаж по j-му маршруту; ступінь кваліфікації i-ої лабораторії при роботі над j-ою науковою темою.

Шукані параметри

1.  – факт призначення або непризначення ресурсу  на роботу :

=   0, якщо і-й ресурс не назначено на J-роботу;

          0, якщо і-й ресурс назначено на J-роботу.

2.  – загальна (сумарна) характеристика якості розподілу ресурсів по роботах.

Таблиця 2.1 – Загальний вигляд транспортної матриці задачі про призначення

Модель задачі про призначення

Специфічна структура задачі про призначення дозволила розробити так званий “Угорський метод” її розв’язування. Тому, хоча в Excel такі задачі розв’язуються звичайним симплексом-методом, у лабораторній роботі потрібно побудувати модель задачі про призначення вигляду (4.1). У деяких випадках, наприклад, коли  – це компетентність, досвід роботи або кваліфікація працівників, умова задачі може потребувати максимізації ЦФ, на відміну від (5.1). У цьому випадку ЦФ  заміняють на  і розв’язують задачу з ЦФ , що рівносильно розв’язанню задачі з ЦФ .

4.2 Постановка задачі

Відділ кадрів підприємства влаштував конкурсний набір фахівців на дві вакантні посади. На ці нові місця (НМ) претендують 3 вже працюючих співробітники (ПС), що зайняті в інших відділах, і 4 нових співробітника (НС). Номери нових співробітників, нових і існуючих місць вибираються за варіантами з табл. 4.2. Номери існуючих місць є номерами вже працюючих співробітників.

Відділ кадрів оцінив за десятибальною шкалою компетентність нових співробітників (табл. 4.3) і вже працюючих співробітників (табл. 4.4) для роботи на нових місцях, і на існуючих місцях (ІМ), тобто зайнятих працюючими співробітниками. Необхідно врахувати, що керівництво підприємства, по-перше, не хоче щоб вже працюючі співробітники претендували на місця один одного, і, по-друге, не має наміру їх звільняти. Необхідно розподілити всіх співробітників за посадами.

4.3 Інструкція до виконання лабораторної роботи

1. Процес приведення задачі про призначення до збалансованого вигляду має свої особливості в порівнянні з ТЗ. Якщо умова збалансованості задачі не виконується через недостачу робіт або виконавців у кількості , то для створення балансу треба ввести таку ж кількість  фіктивних рядків або стовпців.

2. Особливістю розв’язування даної задачі є моделювання системи переваг, що склалася в керівництва підприємства за описаним в умові задачі кадровим питанням.

3. У задачі про призначення, звільнення вже працюючого співробітника або неприйняття на роботу нового співробітника моделюється потраплянням одиниці у фіктивний стовпець матриці розв’язувань задачі, тому для заборони або дозволу в такій ситуації необхідно використовувати відповідні “тарифи”.

4. Значення “тарифів”  вибираються в залежності від напрямку оптимізації ЦФ задачі про призначення ( або ). При цьому керуються принципом “невигідності” заборонених призначень. Так, якщо  – це загальна компетентність працівників, то як заборонні треба вибирати нульові компетентності . А якщо  – це загальний час проходження машинами транспортних маршрутів, то як заборонні треба вибирати значення , що перевищують за величиною максимальні реальні значення .

5. При розв’язуванні задач про призначення в Excel необхідно враховувати, що змінні  є булевими.

4.4 Варіанти

Таблиця 4.2 – Номери співробітників і місць їхньої роботи для конкретного варіанта

Таблиця 4.3 – Компетентність нових співробітників

Таблиця 4.4 – Компетентність вже працюючих співробітників

4.5 Запитання на захист роботи

1.       Яка постановка задачі про призначення?

2.       У чому відмінність моделі задачі про призначення від моделі ТЗ?

3.       Які вихідні і шукані параметри задачі про призначення?

4.       Запишіть математичну модель задачі про призначення.

5.       Як записати модель задачі про призначення, що припускає максимізацію ЦФ?

6.       Яким чином у моделі задачі про призначення можна заборонити конкретне призначення?

7.       У чому особливості процесу приведення задачі про призначення до збалансованого вигляду?

8.       Поясніть модель задачі про призначення, побудовану за заданим варіантом.

9.       Скільки ресурсів необхідно для виконання кожної роботи у задачі про призначення?

10.   В яких випадках актуальна задача про призначення?

11.   Що таке “Угорський метод” розв’язування задачі?

12.   Суть “Угорського методу”.

13.   Суть розв’язування задачі симплексом-методом.

14.   Яким чином довести задачу про призначення до збалансованого вигляду?

15.   Умова збалансованості задачі про призначення.

16.   Що необхідно виконати, якщо умова збалансованості задачі не виконується?

17.   Яка особливість розв’язування даної задачі?

18.   Як вибирається значення “тарифів” у задачі про призначення?

19.   Якого значення набувають змінні x_ij при розв’язуванні задач про призначення?