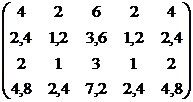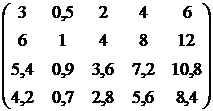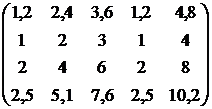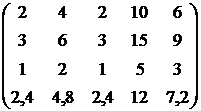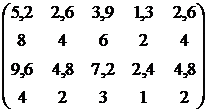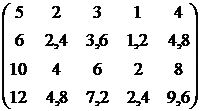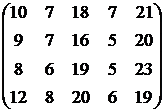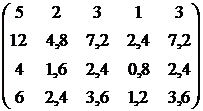|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ЛАБОРАТОРНА РОБОТА №5 ОПТИМАЛЬНИЙ РОЗПОДІЛ ВИРОБНИЧИХ ПОТУЖНОСТЕЙ
Отримання навичок розв’язування двохіндексної
загальної розподільної задачі ЛП і її застосування до оптимального розподілу
виробничих потужностей.
Порядок виконання роботи 1.
Відповідно до номера свого варіанта виберіть умову задачі. 2. Побудуйте
розподільну таблицю для варіанта виробництва без спеціалізації і перетворіть її
в транспортну таблицю. 3. Розв’яжіть
в Excel отриману транспортну задачу і перетворіть отриманий розв’язок в розв’язок
розподільної задачі. 4. Проаналізуйте результати організації виробництва без
спеціалізації і прийміть розв’язування про те, який корпус буде
спеціалізуватися на випуску якого виду продукції. 5. Розв’яжіть
другу підзадачу для варіанта виробництва зі спеціалізацією аналогічно першій
підзадачі (п.1 – 4). 6. Зробіть
вибір оптимального розподілу виробничих потужностей (зі спеціалізацією або без
спеціалізації) на підставі результатів розв’язування обох підзадач. 7. Оформіть
звіт з лабораторної роботи, що повинен містити: – титульний аркуш; – розподільні і
транспортні таблиці обох підзадач із вказанням одиниць вимірювання; – результати розв’язування кожної підзадачі; – висновок про те, який
з варіантів розподілу виробничих потужностей є оптимальним. 5.1 Теоретична
частина
Загальна розподільна
задача ЛП – це розподільна задача, у якій роботи і ресурси (виконавці)
виражаються в різних одиницях виміру. Наприклад, організація випуску
різнорідної продукції на устаткуванні різних типів; організація виконання
набору завдань працівниками різної кваліфікації; організація перевезення
декількох видів товарів на транспорті різних видів і т.д. (двохіндексні
задачі). Вихідні параметри
моделі двохіндексної загальної РЗ 1. n – кількість виконавців (верстатів, працівників,
транспортних засобів і т. д.), m – кількість видів робіт (продукції, що
випускається, перевезених товарів і т. д.). 2. 3. 4. 5. Шукані параметри моделі РЗ 1. 2. 3. Етапи побудови моделі 1. Визначення змінних. 2. Побудова розподільної матриці (табл. 5.1). 3. Завдання ЦФ. 4. Задання обмежень. Таблиця 5.1 – Загальний
вигляд розподільної матриці
Модель двохіндексної загальної РЗ
Таким
чином, формально модель загальної РЗ відрізняється від моделі ТЗ використанням
параметра інтенсивності виконуваних робіт Етапи розв’язування РЗ I. Перетворення
РЗ у ТЗ: а) вибір базового ресурсу і розрахунок нормованих ресурсів
б) перерахування
запасу робочого ресурсу виконавців
в)
перерахування планового завдання
г) перерахування
собівартостей робіт
II. Перевірка
балансу перелічених параметрів III. Пошук
оптимального розв’язку ТЗ IV. Перетворення
оптимального розв’язку ТЗ
де V. Визначення
кількості робіт
VI. Визначення
ЦФ розподільної задачі 5.2 Постановка задачі
На АТ
“Світлана” підготовлені до серійного виробництва 5 нових виробів I1, I2, I3, I4, I5, оптові ціни Витрати на
переустаткування в тис. грн. задаються матрицею
При випуску
виробів зі спеціалізацією витрати
Розгляньте
два варіанти роботи підприємства: без спеціалізації і зі спеціалізацією.
Виберіть найкращий варіант і обґрунтуйте свій вибір. 5.3 Інструкція до виконання лабораторної роботи
Нехай Виробництво без
спеціалізації Розглянемо виробництво
без спеціалізації корпусів. Розподільна матриця такої задачі наведена в табл. 5.2. Таблиця 5.2 – Розподільна
матриця задачі без спеціалізації
При
її побудові необхідно враховувати, що параметр інтенсивності виконання робіт
Наприклад, на
виробництво виробу
Примітка. При розв’язуванні
РЗ у Excel можна обійтися без округлень проміжних значень усіх параметрів
задачі. Для цього розрахунок цих значень необхідно робити прямо у відповідних
осередках. Наприклад, в осередок для На підставі
розподільної табл. 5.2 будуємо модель РЗ – ЦФ (зведені округлені значення) і обмеження:
Перетворимо РЗ у ТЗ. Як базовий корпус можна вибрати будь-який, але ми віддамо
перевагу корпусу з максимальною продуктивністю, тобто корпусу
Перерахуємо фонди часу корпусів
за формулою (5.3):
Перерахуємо планове завдання за формулою (5.4):
Перерахування собівартостей
робимо за формулою (5.5). Наприклад:
Усі
перелічені параметри РЗ зведені в транспортну матрицю задачі без спеціалізації
(табл. 5.3). Перед записом цієї матриці треба перевірити збалансованість
отриманої ТЗ, тобто умову
У даній задачі умова
балансу не виконується, тому що 1914,167 > 1719,167, тобто
Це означає, що фонди
часу корпусів дозволяють зробити більше продукції, ніж це передбачено плановим
завданням. Для одержання балансу додамо в транспортну таблицю фіктивний
стовпець
і фіктивними
тарифами Таблиця 5.3 – Транспортна
матриця задачі без спеціалізації
Примітка.
При розв’язуванні ТЗ у Excel, можливо, прийдеться збільшити відносну похибку розв’язку
в параметрах вікна “Поиск решения”. Оптимальний розв’язок
ТЗ
Оптимальний розв’язок
РЗ
Значення
У даному розрахунку округлення (до меншого цілого)
обов'язкові, оскільки продукція, що випускається, штучна:
Визначимо витрати на
виробництво продукції без спеціалізації:
При розрахунку витрат на виробництво значення у
фіктивному стовпці (рядку) не враховуються. Витрати, розраховані за формулою (5.1)
і формулою (5.10), у принципі, однакові, але в даній задачі будуть трохи
розрізнятися. Це зв'язано з тим, що в (5.10) ми використовували вже округлені
до меншого цілого значення Виробництво зі
спеціалізацією. Щоб прийняти розв’язування про те, який корпус будемо
спеціалізувати і на випуску якої продукції необхідно проаналізувати розподіл
випуску продукції по корпусах, тобто Таким чином,
виникає задача оптимального розподілу продукції по неспеціалізованих корпусах Примітки: 1. У
загальному випадку для відповіді на запитання, чи встигне корпус виконати план
з конкретної продукції, необхідно використовувати дані про фонд часу і
продуктивність корпусу. 2. Якби
корпус Розподільна матриця
задачі без спеціалізації, у якій враховане зменшення витрат на виробництво на
15%, подана в таблиці 5.4. Таблиця 5.4 – Розподільна матриця задачі зі
спеціалізацією
Таблиця 5.5 – Транспортна матриця задачі зі
спеціалізацією
У результаті розв’язування
задачі зі спеціалізацією одержуємо такий оптимальний розподіл виробничих
потужностей і продукції:
Загальні витрати на
виробництво зі спеціалізацією а) витрати на
виробництво 16 400 шт. виробів
б) витрати на
виробництво в інших корпусах в) витрати на
переустаткування спеціалізованого корпусу (матриця S у вихідних даних)
Порівнюючи витрати на
виробництво заданого обсягу продукції без спеціалізації Примітка. При розв’язуванні
подібних задач можлива ситуація, коли після проведення спеціалізації одного з
корпусів виробничих потужностей, інших корпусів не вистачає для випуску іншої
продукції (сумарний перелічений фонд часу менше сумарного переліченого плану
випуску). Тоді внаслідок спеціалізації частина запланованого обсягу продукції
зроблена не буде, що неминуче спричинить за собою втрати прибутку від
незробленої і непроданої продукції. Це приведе до додаткового збільшення
загальних витрат. 5.4
Варіанти
Таблиця 5.6 – Оптові
ціни, фонди часу і план випуску продукції
Витрати на
переустаткування цехів для парних варіантів для непарних варіантів Таблиця 5.7 – Витрати
на виробництво і трудомісткість випуску продукції
Продовження таблиці 5.7
5.5 Запитання на захист роботи
1.
Які вихідні і
шукані параметри моделі двохіндексної загальної РЗ? 2.
Який вигляд
має модель двохіндексної загальної РЗ? 3.
Який економічний
зміст елементів моделі двохіндексної загальної РЗ (змінних, ЦФ, обмежень)? 4.
Яка суть
кожного етапу розв’язування РЗ? 5.
Якими критеріями
необхідно керуватися при виборі корпусу і продукції для спеціалізації? 6.
Як
визначаються усі витрати, зв'язані з виробництвом продукції, у кожному з
варіантів роботи підприємства? 7.
Яка
постановка стандартної транспортної задачі? 8.
Запишіть
математичну модель транспортної задачі. 9.
Перелічіть вихідні і шукані параметри моделі транспортної
задачі. 10.
Яка суть кожного з етапів побудови моделі транспортної
задачі? 11.
Розкрийте поняття збалансованості транспортної
задачі. 12.
Що таке фіктивні і заборонні тарифи? 13.
У якому співвідношенні повинні знаходитися
величини фіктивних і заборонних тарифів при необхідності їхнього одночасного
використання в транспортній моделі? 14.
В чому суть транспортної задачі? 15.
Яке практичне значення транспортної задачі? 16.
Навіщо при розв’язуванні транспортної
задачі додаються фіктивні споживачі або постачальники? 17.
Назвіть приклад використання транспортної
задачі. 18.
Що робити,
коли після проведення спеціалізації одного з корпусів виробничих потужностей,
інших корпусів не вистачає для випуску іншої продукції? 19.
Що Ви розумієте під оптимізацією
розподілу виробничих потужностей? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Назад Зміст Далі | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
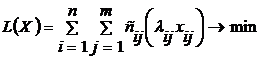
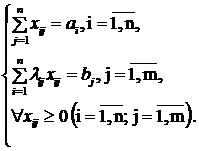
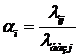 ;
;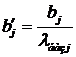
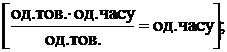
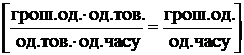 .
.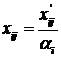
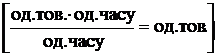 .
. (грн./шт.);
(грн./шт.); (тис. грн.).
(тис. грн.).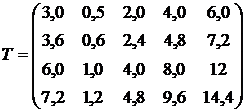 (шт./хв).
(шт./хв).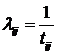
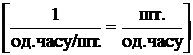 .
.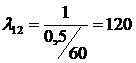
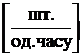 .
.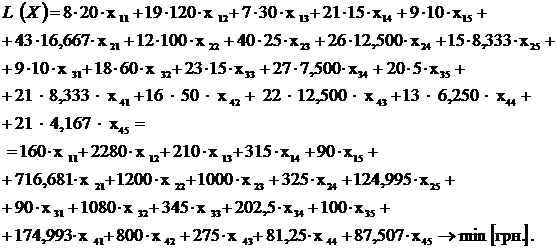
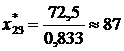
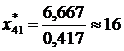
 ;
; .
.