3.1 Перетворення сигналів та їх спектральні характеристики

Інформація сприймається споживачем через сигнали, які генеруються або безпосередньо джерелом, або за допомогою генераторів, що не зв’язані з джерелом (локація). Сигнали мають енергетичну та матеріальну основу – світлові потоки, звукові хвилі, теплове випромінювання, зображення точок, неоднорідності електричного і магнітного полів. Сигналами можуть бути документи, книжки, графіки, таблиці і т. ін. Отже, сигнали різняться за фізичною природою. В електронних системах сприйняття сигналів різної фізичної природи здійснюється первинними перетворювачами, які перетворюють інформаційний параметр в сигнал, що є зручним для подальшої обробки.

Важливий елемент інформаційного процесу – передача інформації. Вона відбувається за допомогою повідомлень – послідовності сигналів в часі або просторі, відповідно повідомлення будуть часові або просторові. Повідомлення складаються із матеріальних елементів, якими вони представлені. Це є абетка повідомлення (знаки, символи, колір, частота, інтенсивність і т. ін.), що містить певну кількість елементів. Передача інформації здійснюється за допомогою переносників інформації. Матеріальну основу переносника інформації складає певний фізичний об’єкт або процес, який характеризується набором параметрів. Один із цих параметрів може стати інформаційним, якщо він змінюється під впливом джерела інформації (модуляція параметра). Власне, після модуляції переносник перетворюється в носія інформації.

Як переносники інформації використовуються коливання різної природи, зокрема – гармонічні коливання, включно з нульовою частотою. В електронних системах знайшли поширення переносники у вигляді коливань електричного струму або напруги – електричні сигнали. Якщо частота коливань дорівнює нулю, є лише один інформаційний параметр – рівень струму або напруги. Якщо частота коливань відрізняється від нуля, інформаційними параметрами можуть бути амплітуда, частота або фаза коливань.

Отже, сигнал – змінна фізична величина, що забезпечує передачу інформації лінією зв'язку.

Загалом всі сигнали розподіляються на детерміновані (невипадкові) і випадкові.

Детермінований сигнал характеризується визначеністю його значень в будь-які моменти часу (задаються певною визначеною функцією часу). Випадковий сигнал характеризується тим, що його значення в будь-який момент часу є випадковими величинами. Випадковими можуть бути як корисні (інформаційні) сигнали, так і шкідливі сигнали – завади, які перешкоджають сприйняттю інформаційних сигналів.

Як приклад детермінованого сигналу можна навести синусоїдальну хвилю, яка графічно описується синусоїдою. Синусоїда – це функція часу , яка записується так:

де величину сигналу визначає коефіцієнт , названий амплітудою;

– кутова частота;

– початкова фаза.

Синусоїда разом з трикутним, пилкоподібним, прямокутним та іншими сигналами належить до періодичних сигналів, тобто до таких сигналів, які повторюють свою форму через деякий сталий проміжок часу.

Будь-який складний періодичний сигнал може бути поданий за допомогою ряду Фур'є як сума простих гармонічних коливань. Сукупність простих гармонічних коливань, на які може бути розкладений складний періодичний сигнал, називається його спектром.

Розподіл амплітуд гармонік за частотою називають амплітудно-частотним спектром або скорочено амплітудним спектром, а розподіл їхніх початкових фаз за частотою – фазочастотним спектром або фазовим спектром.

Лінії дискретного спектра мають розмірність амплітуди сигналу. Безперервний спектр указує на розподіл амплітуд по всьому спектрі й має розмірність щільності амплітуд сигналу.

Якщо спектр сигналу є необмеженим, то при визначенні ширини нехтують гармоніками, амплітуди яких невеликі й не перевищують певного (заданого) рівня. Найбільш часто користуються рівнем 0,707 за амплітудою або 0,5 за потужністю від максимального значення.

Перетворення Фур’є

Перетворення Фур'є – інтегральне перетворення однієї комплексно-значної функції дійсної змінної на іншу, тісно пов'язане з перетворенням Лапласа та аналогічне розкладу у ряд Фур'є для неперіодичних функцій. Це перетворення розкладає дану функцію на осциляторні функції . Використовується для того, щоби розрахувати спектр частот для сигналів змінних у часі (таких як мова або електрична напруга ). Перетворення названо на честь французького математика Жана Батиста Жозефа Фур'є , який ввів це поняття в 1822 році.

Перетворення Фур'є функції математично визначається як комплексна функція , яка задається інтегралом

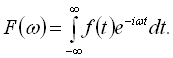
Обернене перетворення Фур'є задається виразом

Серед властивостей перетворення Фур'є можна відмітити такі.

Якщо задані інтегровані функції та і їх відповідні перетворення Фур'є та , тоді перетворення має такі властивості:

а) лінійність;

для довільних комплексних чисел та , якщо , тоді

б) трансляція;

Для довільного дійсного числа , якщо , тоді

в) модуляція;

Для довільного дійсного числа , якщо тоді

г) масштабування;

Для нерівного нулю дійсного числа , якщо , тоді

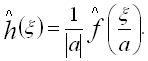
Випадок = -1 приводить до властивості обернення часу, згідно з якою: якщо , тоді

д) спряження;

Якщо , тоді

Зокрема, якщо дійсне, тоді має місце умова дійсності

е) згортка.

Якщо , тоді

Перетворення Фур'є застосовуються для отримання частотного спектру неперіодичної функції, наприклад, електричного сигналу , тобто для подання сигналу у вигляді суми гармонічних коливань . При цьому використовується властивість згортки .

Нехай відгук системи на подразнення у вигляді сигналу буде

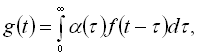
де – певна функція.

Такий запис означає, що відгук системи залежить не тільки від моментального значення збурення, а також від того подразнення, яке було певний час тому, і яке змінило стан системи.

Застосовуючи перетворення Фур'є до обох частин рівняння, отримуємо

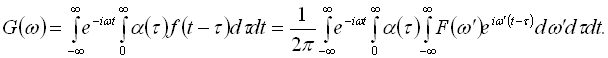
Оскільки

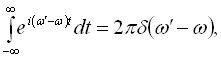
де – дельта-функція Дірака, інтегрування дає

де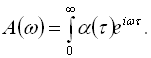

Важливим висновком з цього перетворення є те, що вихідний спектр отримується з вхідного простим множенням на функцію відклику системи .

Спектри періодичних і неперіодичних сигналів

Відомо, що будь-яка періодична функція, яка задовольняє умови Діріхле, може бути подана у вигляді нескінченної у загальному випадку суми гармонічних складових – рядом Фур’є. Умова Діріхле полягає у тому, що: функція повинна бути обмеженою, кусочно-неперервною та мати протягом періоду скінченне число екстремумів.

Відомо дві форми розкладання в ряд Фур’є: тригонометрична й комплексна. Тригонометрична форма розкладання виражається у вигляді

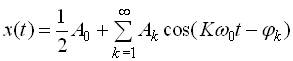де – постійна складова функції ;

– -та гармонічна складова;

– амплітуда, частота та початкова фаза -тої гармонічної складової;

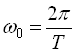– частота основної (першої) гармоніки;

T – період зміни функції .

В математичному відношенні зручніше оперувати комплексною формою ряду Фур’є, поданою у вигляді

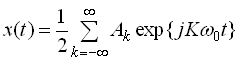де – комплексна амплітуда гармонічної складової частоти .

Комплексна амплітуда визначається через тимчасову функцію за допомогою формули

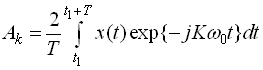Сукупність амплітуд і відповідних частот гармонік прийнято називати спектром амплітуд.

Сукупність початкових фаз і відповідних частот гармонік називають спектром фаз.

На рис. 3.1. подані графічні зображення спектра амплітуд і спектра фаз періодичного сигналу.

Окремі спектральні складові у графічному зображенні спектра амплітуд називають спектральними лініями.

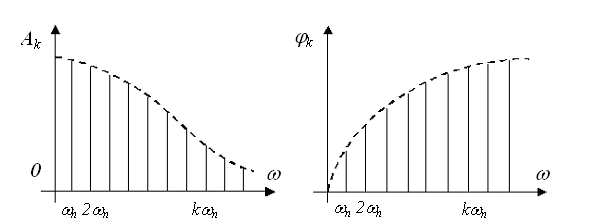
Рисунок 3.1 – Графічні зображення спектра амплітуд і спектра фаз періодичного сигналу

Будь-який неперіодичний сигнал можна розглядати як періодичний, період зміни якого дорівнює нескінченності. У зв’язку з цим розглянутий раніше спектральний аналіз періодичних процесів може бути узагальнений і на неперіодичний сигнал.

Розглянемо як буде змінюватись спектр неперіодичного сигналу при необмеженому збільшенні періоду зміни сигналу. При збільшенні періоду інтервали між суміжними частотами в спектрі сигналу і амплітуди спектральних складових зменшується і в границі при стають нескінченно малими величинами. При цьому спектральний розклад неперіодичного сигналу відображається рядом Фур’є.

Комплексна форма неперіодичного сигналу має вигляд

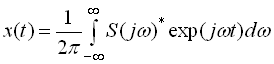де – спектральна щільність сигналу;

– амплітудно-частотна характеристика сигналу;

– фазочастотна характеристика сигналу.

Попередній вираз називається формулою оберненого перетворення Фур’є.

Подання неперіодичної функції інтегралом Фур’є можливе при виконанні таких умов:

1) функція задовольняє умову Діріхле;

2) функція абсолютно інтегрована

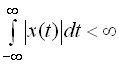Таким чином, спектр неперіодичного сигналу, на відміну від спектра періодичного сигналу, є суцільним і являє собою суму нескінченної кількості гармонічних складових із нескінченно малими складовими.

Амплітуди гармонічних складових можуть бути подані у такому вигляді

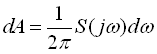звідки спектральна щільність визначається виразом

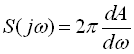Спектральна щільність пов’язана з функцією часу через пряме перетворення Фур’є

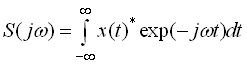Спектральна щільність однозначно відображає неперіодичний сигнал і задовольняє умову: .

Модуль спектральної щільності є парною, а аргумент непарною функцією частоти

Спектри одиничних та періодичних імпульсних послідовностей

Аналіз перехідних процесів в колі при дії на нього складної (негармонічної) ЕРС класичним методом виявляється досить складним. Більш зручними в таких випадках є методи, основані на спектральному поданні зовнішньої ЕРС і принципі суперпозиції. Тому, перш ніж переходити до аналізу таких перехідних процесів, розглянемо спектри деяких найбільш важливих для радіотехніки періодичних та неперіодичних ЕРС.

Будь-яку функцію , задану в інтервалі , і яка періодично повторюється з частотою 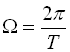, де – період повторення, та таку, що задовольняє умову Діріхле, можна подати рядом Фур’є, який можна записати або в тригонометричній формі

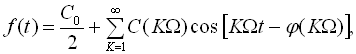
де ,

або в комплексній формі

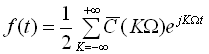де – комплексна амплітуда -ї гармонічної складової;

– модуль цієї величини, чи просто амплітуда;

– початкова фаза -ї гармонічної складової.

Величина – середнє за період значення функції чи постійна складова складної ЕРС

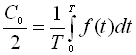Розглянемо основні величини, що характеризують спектр складної періодичної ЕРС. Комплексна амплітуда, яка входить в ряд Фур’є, визначається як

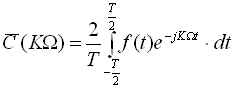Залежність модуля комплексної амплітуди від частоти зображають у вигляді графіка, який називається амплітудно-частотним спектром (рис. 3.2, а). Тут кожній частоті відповідає лінія, величина якої вказує амплітуду гармонічної складової.

Залежність початкової фази від частоти зображають у вигляді фазочастотного спектра (рис. 3.2, б). Як видно з рис. 3.2, для складної періодичної ЕРС, спектр є лінійчатим чи дискретним. Тут лінії розміщенні по шкалі частот так, що відділені на відстань , яка дорівнює частоті повторення ЕРС. Зберігаючи незмінним амплітудно-частотний спектр, але змінюючи вигляд фазочастотного спектра, ми тим самим змінюємо форму складної періодичної ЕРС, яка зображена цими спектрами. При розгляді спектра складної ЕРС часто обмежуються одним графіком, на якому
зображено амплітудно-частотний спектр з вказуванням фаз гармонічних складових.

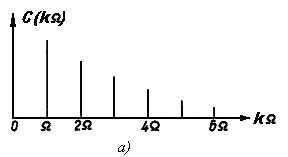
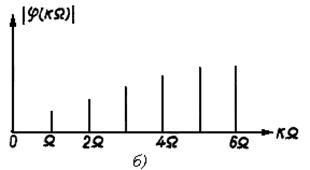
Рисунок 3.2 – Амплітудно-частотний та фазочастотний спектри

Теорема про суму спектрів і теорема запізнення дозволяють обчислити спектр групи однакових рівновідстаючих імпульсів. Нехай є два однакових імпульси і , розділених інтервалом часу . Можна записати спектральну функцію другого імпульсу через спектральну функцію першого:

Тоді на основі виразу для спектральної функції суми двох імпульсів отримаємо:

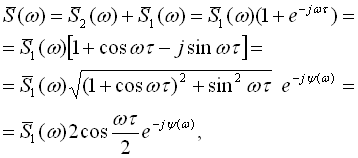
де .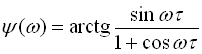

Зі збільшенням кількості імпульсів спектр групи імпульсів наближається за структурою до лінійчатого спектра періодичної послідовності імпульсів.

Практично всі канали зв’язку мають обмежену смугу пропускання. Отже, при передачі сигналу через реальний канал зв’язку може бути передана лише частина його частотного спектра.

За практичну ширину спектра сигналу приймають діапазон частот, в межах якого знаходиться найбільш вагома частина спектра сигналу. Вибір практичної ширини спектра сигналу визначається двома критеріями: енергетичним критерієм та критерієм допустимих спотворень форми сигналу.

Розглянемо для прикладу послідовність прямокутних імпульсів тривалістю , амплітудою h, із періодом проходження Т (рис. 3.3).

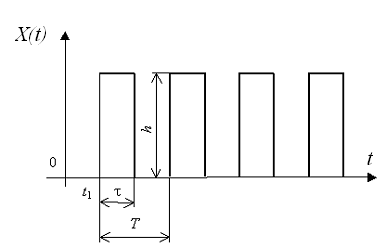
Рисунок 3.3 – Прямокутні імпульси

Розклад в ряд Фур’є періодичної послідовності прямокутних імпульсів подаєтьсяу вигляді

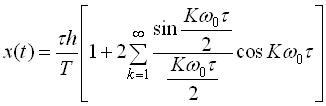Спектр амплітуд такого сигналу показаний на рис. 3.4.

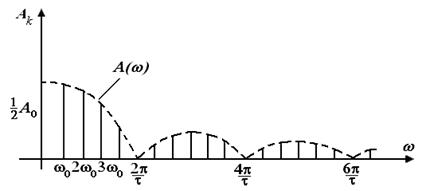
Рисунок 3.4 – Спектр амплітуд

Обвідна його визначається рівнянням

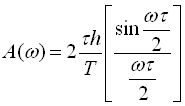де – для К-ої гармоніки.

Можна показати, що для періодичної послідовності імпульсів прямокутної форми тривалістю достатньо практичну ширину спектра вибрати рівною 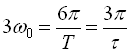. В цій області частот зосереджено 95% всієї потужності сигналу. Розглянемо одиничний прямокутний імпульс тривалістю Т та величиною h, спектральна щільність такого сигналу визначається виразом

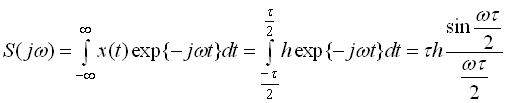Енергія сигналу, зосереджена в смузі частот від 0 до ,

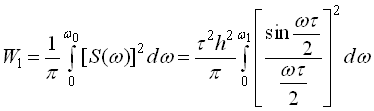Для оцінювання впливу ширини смуги пропускання каналу зв’язку на викривлення форми сигналів розглянемо проходження прямокутного імпульсу тривалістю Т та величиною U через канал зв’язку, що являє собою ідеальний фільтр низьких частот. Коефіцієнт передачі цього фільтра виражається залежністю: , при цьому в діапазоні частот модуль коефіцієнта передачі і аргументу ; поза цим діапазоном .

В теорії кіл показано, що вихідний сигнал в цьому випадку може бути поданий в аналітичному вигляді

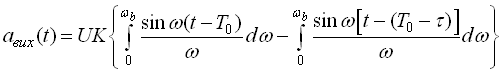Форми переднього й заднього фронтів імпульсу спотворюються однаково. На рис. 3.5 показана форма переднього фронту вихідного сигналу.

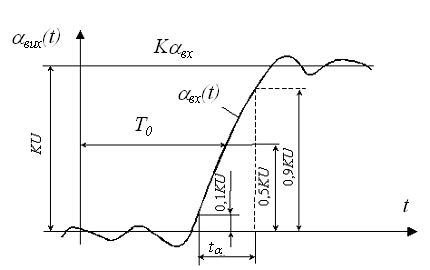
Рисунок 3.5 – Форма переднього фронту вихідного сигналу

Щоб вихідний сигнал зміг досягнути найбільшого значення, активна тривалість переднього фронту повинна бути не більша тривалості вхідного імпульсу. При цьому, як показав аналіз, повинна бути справедлива умова 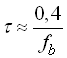або .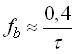

Дискретне перетворення Фур’є

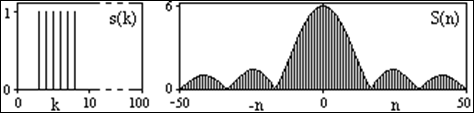
Припустимо, що замість функції неперервної змінної задано функцію дискретної змінної на рівномірній гратці (рис. 3.6), тобто задано значення функції для скінченної послідовності значень аргументу – таблиця функції Тут за допомогою 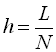позначено крок гратки – відстань між сусідніми вузлами.

Перетворення Фур’є такої функції можна означити як суму

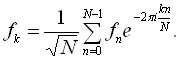
Рисунок 3.6 – Дискретний сигнал та модуль його спектра

Варто зазначити, що недоцільно використовувати суму з кількістю членів, більшою за кількість вузлів гратки.